Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный машиностроительный университет "МАМИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Е. Н. Яшин Анализ и Синтез Дискретных Систем

.pdf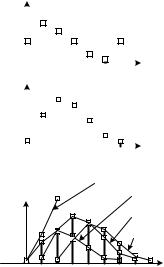

Скачиваний:

Добавлен:

27.03.2016

Размер:

1.06 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

сказать, что реакция ДС будет умножена на эту же константу. Ввиду того, что ДС обладает импульсной характеристикой, то она будет сохранять последствия прошедшего импульсного воздействия ещё некоторое время,

втечение которого на вход ДС может поступить следующий импульс.

Всоответствии со свойством линейности реакция ДС на входное воздействие будет равна сумме реакции на текущее воздействие и реакции системы от предыдущих воздействий в рассматриваемый момент времени:

k	k
y(k ) = h(k )Ä x(k ) = ∑h(m)x (k - m) = ∑h(k - m)x (m) ,		(2.1)
m=0	m=0

где Ä – оператор дискретной свёртки. Выражение (2.1) называется дискретной свёрткой и широко используется для расчёта реакции дискретной системы. В формуле (2.1) в целях упрощения записи опущен период дискретизации Td . В качестве примера на рис. 2.2 показан процесс нахожде-

ния свёртки для момента времени k = 2.

Если в качестве входного воздействия взять s(t) , то можно установить связь между импульсной и переходной функцией:

s(k ) = h Ä s = ∑h(m) .

(2.2)

m=0

Воздействие

Импульсная

характеристика

0	Td	2Td	3Td	t
			Сумма реакций
	y			Реакция k=00
	y			Реакция k=11
				Реакция k=11
				Реакция k=22
0	Td	2Td	3Td	t
Рис. 2.2. Нахождение свёртки для k = 2

2.2. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ

По аналогии с непрерывными системами, математические модели

которых описываются дифференциальными уравнениями, ДС представля-

ются линейными разностными уравнениями. Понятию производной в ана-

логовой системе соответствует конечная разность в дискретной системе,

а непрерывной функции –

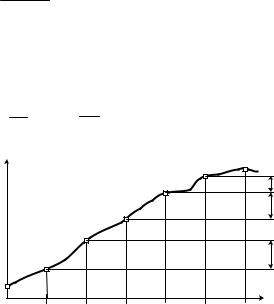
последовательности отсчётов. На рисунке 2.3

показан дискретный процесс Y

с периодом дискретизации

Td . Нулевая

конечная разность равна значению дискретной функции

0 yi

= yi . Первая

конечная

разность

равна

разности

нулевых

конечных

разностей

1 yi =

0 yi

−

0 yi−1 = yi

− yi −1

и по своему смыслу соответствует прира-

щению дискретной функции за период дискретизации (первой производ-

ной при нормированном периоде дискретизации). Вторая конечная

разность

2 yi

1 yi

−

1 yi −1 = (yi

− yi−1 )− (yi−1 − yi−2 ) = yi

− 2 yi−1 + yi −2 .

В общем случае

k yi =

k −1 yi −

k −1 yi−1 , которую можно выразить через

значения дискретной функции следующим образом

y = y − ky

−1

+ C2 y

−2

− C3 y

+ K − C k −1 y

+ y

−k

(2.3)

k i

k i−3

i −k +1

где Ckr =

–

число сочетаний из k по r ( k ³ r ).

r!(k - r)!

Для линейных систем конечно-разностное уравнение устанавливает

линейное соотношение между входными и выходными дискретными про-

цессами и по своей структуре соответствует линейному дифференциаль-

ному уравнению

0 yi + a1

1 yi + K + an

n yi

= b0

0 xi + b1

1xi + K + bm

m xi ,

(2.4)

где a j , j = 0, n , bj , j = 0, m –

параметры дискретной системы.

yi−1

yi−2

yi −1

yi−k+1

yi − k

yi − k +1

(i − k )T (i −k +1)T (i −2)T (i−1)T

Рис. 2.3. К понятию конечных разностей

Раскрывая конечные разности (2.4) по формуле (2.3), получим разностное уравнение

yi +

yi−1 + K+

yi−n =

xi +

xi−1 + K+

xi−m .

2.5)

Разностное уравнение (2.5), в отличие от дифференциального, решается методом прямой подстановки известных рядов начальных значений и входного процесса, поэтому оно непосредственно описывает алгоритм вычисления реакции по известному входному воздействию. Решение разностного уравнения (2.5) можно записать в виде суммы

y	= y0	+ y X	,	(2.6)
i	i	i

которая состоит из дискретного переходного процесса yi0 и вынужденного процесса yiX . Переходной процесс представляет собой собственное движение системы под воздействием начальных условий yi−1, K, yi−n и отсутствии внешних воздействий:

yi +

yi −1 + K +

yi−n = 0 .

(2.7)

Переходной процесс представляет собой частное решение при нулевых начальных условиях и заданном входном воздействии xi , K, xi−m :

yi =

xi +

xi−1 + K+

xi−m .

(2.8)

Похожесть структуры и характера решения линейных дифференциальных и конечно-разностных уравнений приводит ко многим аналогиям в методиках исследования непрерывных и дискретных систем.

Решив (2.5) относительно yi , получим уравнение в рекуррентной форме

∑

b j

xi− j

− ∑

a j

yi− j

(2.9)

j=1

j=0

которое представляет собой алгоритм непосредственного нахождения реакции дискретной системы. Уравнение (2.9) относится к рекурсивному типу (дискретные системы с обратной связью), так как в нём учитываются реакции системы в прошлые моменты времени, в противном случае оно будет относиться к нерекурсивному типу.

Уравнение (2.5) можно решить и в аналитическом виде [1]. Для этого решение однородного уравнения (2.7) ищется в виде y(t ) = λt . Подставив это решение в (2.7), получим

a0λiTd + a1λ(i−1)Td + K+ an λ(i−n)Td = 0

или

(a0 + a1λ−Td + K+ an λ−nTd )λiTd = 0 .

Произведя замену z = λTd , это уравнение приводится к виду

z −1 +K+

z −n = 0 ,

или умножив на z n :

z n +

z n−1

+ K+

= 0 ,

(2.10)

которое называется характеристическим

уравнением, корни

которого

zk = λTkd . А решением однородного разностного уравнения (2.7) будет

t y(t ) = λtk = zkTd .

Если все корни zk , k = 1,n характеристического уравнения (2.10) про-

стые (т.е. различные), то общее решение разностного уравнения (2.7) имеет вид

n	t
y0 (t ) = ∑Ck zkTd ,		(2.11)

k =1

где Ck – произвольные постоянные, которые определяются из начальных условий системы. Если среди корней характеристического уравнения имеется кратный корень zl кратности ml , то ему в (2.11) соответствует слагаемое


C l		+ C l	t
C l		+ C l
	1	2	Td
			Td

				t	ml	−1	t
		l		t			T
+	K	l					d	.	(2.12)
	K						d
		+ Cml				zl
			td

Простые комплексно-сопряжённые корни							zk , k +1 = α ± jβ можно за-
менить на одно слагаемое
	t		t			t

ρTd Acos				ϕ	+ Bsin		ϕ ,	(2.13)

		T			T
			d			d

					β
	2		2		β
где ρ = α		+ β		, ϕ = arctg		,	A, B – произвольные константы.
где ρ = α		+ β		, ϕ = arctg		,	A, B – произвольные константы.
					α

Пример. Пусть дискретная система описывается разностным уравнением 2 yi + yi−1 − 3yi −2 = xi + 4xi−1 . Найти реакцию системы на дискретную

дельта-функцию, если она находилась в состоянии покоя.

Решение. Представим разностное уравнение в рекуррентной форме

yi = 0,5xi + 2xi−1 − 0,5 yi −1 + 1,5yi−2 .

Так как до подачи воздействия система находилась в состоянии покоя, то yi −1 = yi −2 = 0 . Пусть воздействие поступило в момент времени

i = 0 , тогда непосредственной подстановкой можно найти реакцию в последующие моменты времени (табл. 2.1).

2.1. Расчёт реакции на дискретную дельта-функцию

i	xi					yi
–2	0	0
–1	0	0
0	1	y0 = 0,5x0 + 2x– 1 – 0,5 y– 1 + 1,5y– 2 = 0,5×1 = 0,5
1	0	y1 = 0,5x1		+ 2x0	– 0,5 y0	+ 1,5y– 1 = 2×1 – 0,5 ×0,5 = 1,75
2	0	y2 = 0,5x2		+ 2x1	– 0,5 y1	+ 1,5y0 = –0,5 ×1,75 + 1,5×0,5 = –0,125
3	0	y3	= 2,6875
4	0	y4	= –1,53125

В таблице 2.1 приведены значения yi для i = - 2, 4 , из которых сле-

дует, что реакция системы имеет колебательный характер бесконечной длительности. Так как в качестве входного воздействия бралась дискретная дельта-функция, то рассчитанная реакция ДС есть не что иное, как импульсная характеристика ДС.

Аналитическое решение данного разностного уравнения можно представить в форме (2.6) y(t ) = y0 (t)+ y X (t ).

Для нахождения y0 (t ) решается уравнение 2 yi + yi−1 − 3yi−2 = 0 , ха-

рактеристическое уравнение которого 2z 2 + z − 3 = 0 имеет два корня z1 = 1, z2 = −1,5 . Тогда общее решение запишется в виде

y0 (t) = C11t + C2 ×(-1,5)t = C1 + C2 (-1,5)t .

Функция y X (t) представляет собой решение разностного уравнения

при известном входном воздействии. В рассматриваемом случае входным воздействием является дискретная дельта-функция в момент времени t = 0 . Так как в этом случае входное воздействие присутствует только в определённые моменты времени, то можно считать, что системе придаются новые начальные условия в эти моменты, а в остальное время она

функционирует как свободная, т.е. y(t) = y0 (t) + y X (t) . Для данного уравнения такими моментами будут t = 0, t = 1 .

При t = 0 имеем 2 y0 + y−1 − 3y−2 = 1 , откуда y0 = 0,5 .

При t = 1 имеем 2 y1 + y0 − 3y−1 = 4 , откуда y1 = 1,75 . Тогда

y(1) = 1,75 = C1 + C2 (-1,5)1 = C1 -1,5 ×C2 ,

y(0) = 0,5 = C1 + C2 (-1,5)0 = C1 + C2 .

Решение данной системы даёт C1 = 1 и C2 = -0,5 . Окончательно по-

лучим y(t) = 1- 0,5 ×(-1,5)t . Результаты расчётов по данной формуле приведены в табл. 2.2.

2.2. Расчёт реакции системы по аналитическому решению

t	y(t) = 1 - 0,5 × (-1,5)t

0	0,5

1	1,75

2	–0,125

3	2,6875
4	–1,53125
5	4,796875

2.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ДИСКРЕТНОГО СИГНАЛА

Преобразование Лапласа для непрерывных систем позволяло перейти от дифференциального уравнения n-го порядка к степенному ряду n-го порядка, что существенно упрощало анализ и синтез непрерывных систем. Для дискретных систем естественным продолжением, таким образом, будет переход от разностного уравнения к аналогичному степенному ряду.

В случае дискретных систем значение дискретного сигнала во вре-

∞

мени можно представить как fd (t) = f (t) ∑ δ(t − kTd ) . Тогда преобразо-

k =−∞

вание Лапласа этого сигнала будет

∞	∞	∞
Fd (p) = ∫ f	(t ) ∑ δ(t − kTd )e− pt dt =	∑ f (kTd )e− pkTd ,	(2.14)
t =0	k =−∞	k =−∞
где p = σ + jω – комплексное число.
Введя обозначение
	e pTd = z ,		(2.15)
выражение (2.14) можно привести к виду
	∞
Fd (z) = Z [ f (kTd )]= ∑ f (kTd )z −k ,			(2.16)

k =−∞

откуда следует, что дискретный процесс можно выразить в виде степенного ряда путём замены переменных (2.15), что по аналогии с непрерывными системами означает переход от конечно-разностных уравнений n-го порядка к степенному ряду n-го порядка. Выражение (2.16) получило название z-преобразования и играет такую же роль для дискретных систем, что и преобразование Лапласа для непрерывных систем. Z-преобразование определено для тех z, при которых ряд (2.16) сходится. Значения z, при которых Fd (z) = ±∞ называются полюсами.

Если действительная часть комплексного числа σ = 0 , то z = e jωTd и ряд (2.16) запишется как дискретное преобразование Фурье, которое связывает спектр дискретного сигнала с его отсчётами

∞
S (w) = Fd (e jωTd )= ∑ f (kTd )e	− jωkTd .	(2.17)

k =−∞

2.4.ПРИМЕРЫ Z-ПРЕОБРАЗОВАНИЯ

1.Дискретная дельта-функция

x(k ) = 1, k = 0 ;
0, k ¹ 0;
∞
X (z) = ∑ x(k )z −k	= 1× z −0 = 1 .		(2.18)
k =−∞
Область сходимости этой функции –	вся комплексная плоскость.
2. Дискретный единичный скачок
x(k ) = 1, k ³ 0;
0, k < 0;
∞	∞
X (z) = ∑ x(k )z −k = ∑z		−k .	(2.19)
k =−∞	k =0

Ряд (2.19) является суммой геометрической прогрессии, первый член которой равен 1× z−0 = 1 , которая сходится при значении её знаменателя z −1 < 1 , что соответствует z > 1 , тогда

X (z) =			1	.		(2.20)
X (z) =		1- z−1		.		(2.20)
3. Экспоненциальная функция
		k	, k ³ 0;
x(k ) = a			, k ³ 0;
	0, k < 0;
					−1z)−k .
∞			∞
X (z) = ∑ ak z −k			= ∑(a			(2.21)
k =−∞			k =0

Ряд (2.21) представляет собой геометрическую прогрессию с первым членом, равным 1, и знаменателем az −1 , который сходится при az −1 < 1 ,

или z > a :

X (z) =	1
X (z) =	1- az−1 .	(2.22)

Для большого числа дискретных сигналов результаты z-преобра- зования сведены в табл. 2.3.

Таблица 2.3

№ п/п

Дискретная

Результат

Область

последовательность x(n), n ³ 0

z-преобразования X(z)

сходимости

kδ(n)

z > 1

z −1

z > 1

(z −1)2

kn2

kz(z + 1)

z > 1

(z −1)3

ke–an

z > e–a

z − e−a

–an

kze−a

–a

kne

z > e

(z − e−a )2

–an

z(1− e−a )

–a

1 – e

z > e

z2 − z(1+ e−a ) + e−a

cos(an)

z(z − cos a)

z > 1

z2 − 2z cos a + 1

sin(an)

z sin a

z > 1

z2 − 2z cos a + 1

e–an sin(an)

ze−a sin a

z > e–a

2 − 2ze−a cos a + e−2a

–an

ze−a (ze−a − cos a )

–a

e cos(an)

z > e

2 − 2ze−a cos a + e−2a

ch(an)

(z2 − z ch a)

z > ch a

z2 − 2z ch a +1

sh(an)

z sh a

z > sh a

z2 − 2z ch a + 1

kan

z > a

z − a

knan

kaz

z > a

(z − a)2

n cos(n pa

+ ca )

e jca

e− jca

z −

e jpa

z −

e− jpa

2.5. ОСНОВНЫЕ СВОЙСТВА Z-ПРЕОБРАЗОВАНИЯ

1. Линейность. Если Z [x1 (i)] = X1 (z ) и Z [x2 (i)]= X 2 (z) , то

Z [ax1 (i)+ bx2 (i)] = aX1 (z)+ bX 2 (z).

2. Задержка на n-тактов. Если y(i) = x(i - n), то

∞		∞	∞	−(i−n) =
Y (z) = ∑ y(i)z	−i =	∑ x(i - n)z	−i = z−n ∑ x(i - n)z	−(i−n) =
i =−∞		i =−∞	i = −∞

∞

= z −n ∑ x( j)z − j = z−n X (z).

j=−∞

Откуда следует, что при задержке (некоторой последовательности на

n-тактов необходимо умножить её z-преобразование на z −n , который называется оператором задержки на n-тактов.

∞

3. Свёртка сигналов. Пусть y(i) = h(i) Ä x(i) = ∑ h(k )x(i - k ) является

k =−∞

свёрткой двух бесконечных дискретных последовательностей, тогда

Y (z) =

∞

y(i)z−i

∞

∑

h(k )x(i - k )z−i =

i =−∞

i= −∞ k =−∞

∞

h(k )x(i

- k )z−k z

−(i −k )

∑

i =−∞ k = −∞

(2.23)

∞

x(i - k )z

∑

h(k )z−k

−(i −k ) =

k = −∞

i= −∞

∞

= X (z) ∑ h(k )z−k = X (z)H (z).

k =−∞

То есть z-преобразование свёртки двух дискретных процессов равно произведению их z-преобразований. Это уравнение играет большую роль

втеории дискретных систем.

4.Дифференцирование. Если X (z) = Z [x(k )] , то z-образ последова-

тельности kx(k) можно найти, продифференцировав X (z):

Z [kx(k )]= -z dX (z).

p-плоскость

jω

z-плоскость

IIm(z))

ω =

ωd

ω =

ω = 0

ω=ωd

Re(z)

ω =

3ωd

= ωd

ω =

3ωd 4

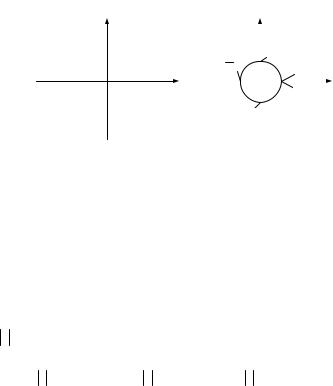
Рис. 2.4. Отображение p-плоскости в z-плоскость

5. Связь с преобразованием Лапласа. Вводя						замену e pTd = z , где
p = σ + jω является комплексной переменной Лапласа, то
			z = e(σ+ jω)Td = eσTd e jωTd .
Откуда				2π			ω
	z	= e	σTd , а arg(z) = ωT = ω		= 2π			,


			d	ωd			ωd

где ωd – круговая частота дискретизации. При изменении ω от −∞ до ∞ в z-плоскости будут отображаться концентрические окружности с радиусом z = eσTd . Так как Td > 0 , то для этого радиуса справедливы следующие соотношения

z = 1 при σ = 0; z < 1 при σ < 0; z > 1 при σ > 0,

из которых следует, что мнимая ось р-плоскости переходит в окружность единичного радиуса в z-плоскости, левая сторона p-плоскости отображается внутрь единичного круга z-плоскости, а правая сторона p-плоскости – на внешнюю сторону единичной окружности z-плоскости (рис. 2.4).

2.6. ОБРАТНОЕ Z-ПРЕОБРАЗОВАНИЕ

Обратное z-преобразование Z −1 позволяет восстанавливать дискретную последовательность по её z-образу:

x(k ) = Z −1[X (z)].

Умея проводить обратное z-преобразование, можно выразить исходные дискретные последовательности в виде степенных рядов, провести с ними необходимые алгебраические вычисления с целью получения z- образа выходного сигнала, и затем преобразовать их в дискретную последовательность.

Если z-образ имеет вид степенного ряда, то обратное z-преобразование находится путём определения коэффициентов у операторов задержки z −n .

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.09.201943.42 Кб10доклад по налогам..docx
#
18.08.201996.26 Кб0Документ Microsoft Word 1234.doc
#
26.08.2019180.22 Кб4Документирование, брошюра, методичка.doc
#
16.11.2019172.54 Кб4Дом. зад. и вопросы к зачету для заочн.doc
#
19.09.201945.73 Кб2доп вопросы 1-4.docx
#
27.03.20161.06 Mб35Е. Н. Яшин Анализ и Синтез Дискретных Систем.pdf
#
05.06.201519.02 Mб10Е.ИНТО. Раздел.1.doc
#
28.04.2019140.29 Кб58Заболевания органов пищеварения у детей.doc
#
19.11.2019715.78 Кб7загр в-ва Лекц3.doc
#
31.08.2019212.48 Кб2Задания ГЭК11 справочные.doc
#
11.09.20191.19 Mб12Задания_по статистике.doc