3.3. Моделирование транспортных сетей и расчет кратчайших расстояний

При планировании перевозок возникает необходимость в определении кратчайших расстояний между АТО, пунктами потребления и пунктами отправления грузов. Расстояния между пунктами являются основой для оплаты клиентами транспортных услуг, учета расхода топлива, определения грузооборота АТО, расчета заработной платы водителей и т.д.

Множество всех дорог города или района составляют дорожную сеть. Транспортная сеть – это совокупность дорог региона, пригодных для движения заданных транспортных средств. Транспортная сеть всегда является частным случаем дорожной сети и, как правило, строится для различных типов транспортных средств.

Модель транспортной сети может быть представлена в виде графа. Граф – это фигура, состоящая из точек (вершин) и соединяющих их отрезков (звеньев). Вершины графа – это точки на сети, наиболее важные для определения расстояний или маршрутов движения.

Звенья графа – это отрезки транспортной сети, характеризующие наличие дорожной связи между соседними вершинами. Звенья графа характеризуются числами, которые могут иметь различный физический смысл. Чаще всего это расстояние, но может использоваться, например, и время движения или стоимость проезда. Ориентированные по направлению звенья графа называются дугами.

Моделирование транспортной сети начинают с размещения вершин графа. За вершины графа принимают ГОП, ГПП, центры крупных жилых кварталов или небольших обособленных жилых пунктов и пересечения улиц. Каждой вершине присваивается порядковый номер или другое условное обозначение. После размещения вершин их связывают дугами или звеньями.

Сформулируем задачу о кратчайшем пути. Пусть дан связанный граф, имеющий R вершин и N ориентированных дуг, причем каждой дуге поставлено в соответствие неотрицательное число С_ij, называемое ее длиной. Требуется найти на графе кратчайшие пути и их длины от заданной вершины i₀ до всех остальных вершин. В каждую вершину графа может входить только одна дуга, принадлежащая какому-нибудь кратчайшему пути.

Все алгоритмы решения этой задачи являются итерационными (повторяющимися), в которых на каждой итерации корректируется уже построенное множество кратчайших путей между вершинами графа.

Метод потенциалов для определения кратчайших расстояний заключается в следующем. Начальной вершине сети, за которую может быть принята любая из вершин, присваивают потенциал, равный нулю. Затем определяют потенциалы соседних с начальной точкой вершин сети. Значение потенциала равно расстоянию до вершины. Выбирают наименьший потенциал и присваивают его соответствующей вершине. Затем вычисляют потенциалы вершин, соседних с выбранной, и снова выбирают наименьший потенциал и присваивают его соответствующей вершине и т.д.

Полное решение задачи включает в себя столько шагов, сколько вершин имеет транспортная сеть, поскольку на каждом шаге определяют потенциал или кратчайшее расстояние от начальной точки до одной из вершин сети.

3.4. Формулировка транспортной задачи

Оптимальное закрепление поставщиков однородного груза за потребителями, т.е. нахождение оптимальных грузопотоков, является классическим примером транспортной задачи. Эта задача возникает, когда несколько поставщиков имеют однородный груз, который в определенных объемах должен быть доставлен потребителям.

Суть транспортной задачи линейного программирования состоит в следующем. В пунктах отправления А₁, А₂,..., А_п имеется однородный груз в количестве а₁, а₂,..., а_п. Этот груз необходимо доставить в пункты потребления В₁, В₂,..., В_т в количестве b₁, b₂,..., b_т. Известны кратчайшие расстояния с_ij, между всеми пунктами отправления и получения груза. Необходимо построить план перевозок таким образом, чтобы была удовлетворена потребность в грузе всех пунктов потребления, был вывезен весь груз из пунктов производства и при минимуме транспортной работы в тонна-километрах.

Экономико-математическая модель транспортной задачи выглядит следующим образом. Система ограничений по количеству груза, доставляемого в пункты потребления:

Система ограничений по количеству груза, вывозимого из каждого пункта производства:

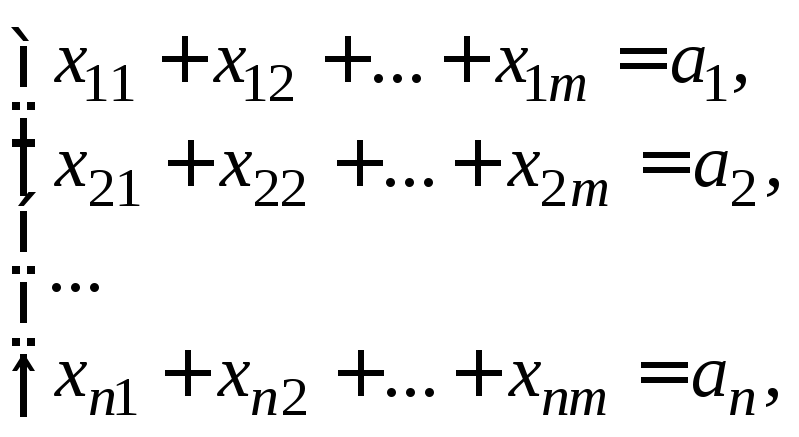
где x_ij – объем перевозок между i-и и j-й точками транспортной сети; i – количество поставщиков; j – количество потребителей; а_i – ограничения по предложению; b_j – ограничения по спросу.

Причем предполагается, что , так как это необходимо для совместимости системы уравнений. Общий объем транспортной работы (стоимости перевозок) должен быть минимальным. Поэтомуцелевая функция выглядит следующим образом: , гдеx_ij  0.

Математическая постановка задачи показывает, что задача закрепления поставщиков за потребителями относится к классу задач линейного программирования, называемой транспортной задачей линейного программирования. Условия транспортной задачи обычно представляются в виде матрицы, образец которой приведен в табл. 3.1.

Т а б л и ц а 3.1