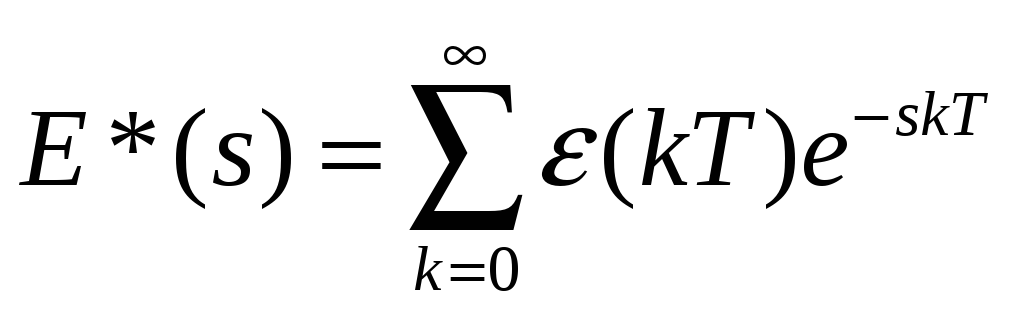1. Математическое описание процесса квантования.

(в лекциях p=τ, u=r)

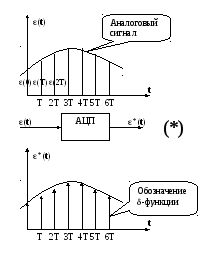
Т – период дискретности (квант);

Т=const

р – ширина импульса

Будем считать, что р  0.

В таком случае нужно переходить к -функции.

(*–квантованный сигнал)

р = площадь -функции.

запишем u*(t) как сумму -функций

u*(t) =(t-kT)

*(t) = (t)u*(t) =(kT)(t-kT)

*(t) =  0 (kT)(t-kT)

Дискретизацию (квантование) на схемах изображают так:

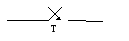
Запишем преобразование Лапласа дискретного по времени сигнала:

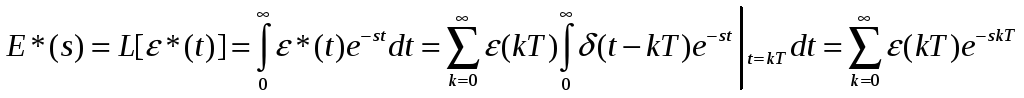
Вычисление этого преобразования – очень трудоемкий процесс.

Другой способ вычисления – используя преобразование Фурье:

;

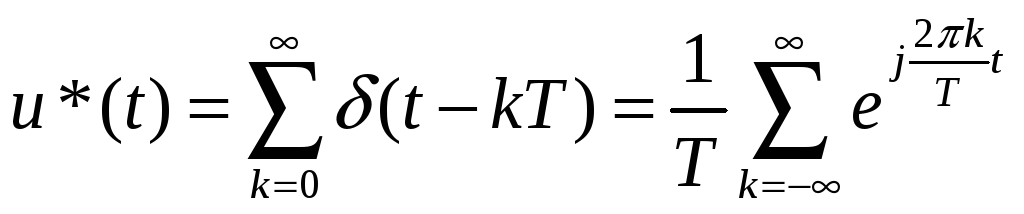
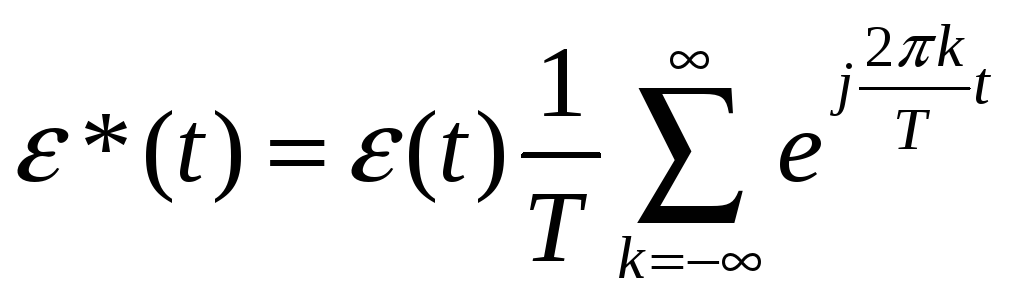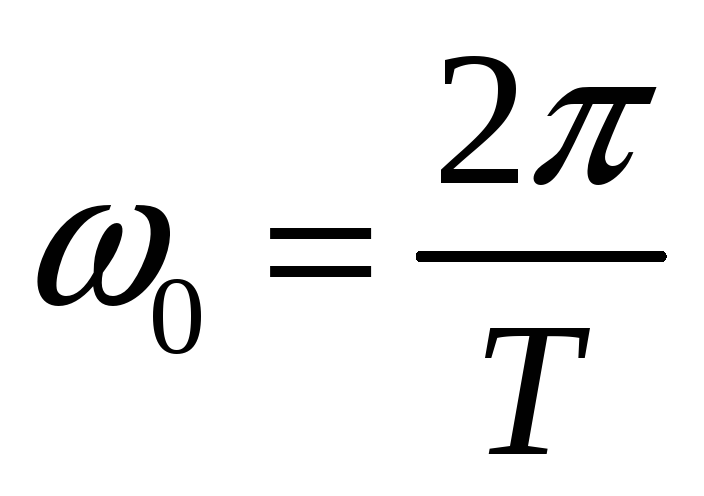
Все равно бесконечный ряд. Но здесь ценна физическая трактовка.

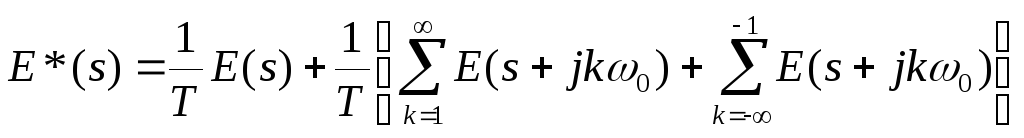
В фигурных скобках – ВЧ составляющие.

– не существует

Таким образом, не существует передаточной функции идеального квантователя

(при условии, что стоит фильтр низких частот)

Формула очень грубая, но в первом приближении ее можно теоретически рассматривать.

2. Передаточные функции аналого-цифровых и цифро-аналоговых преобразователей.

А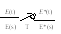ЦП.

Применим ряды Фурье:

Преобразование Лапласа:

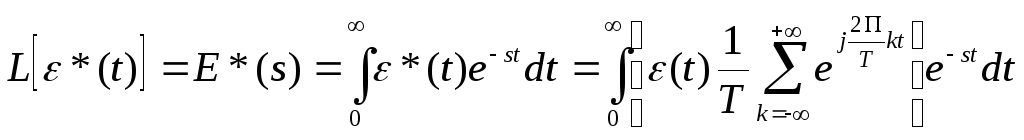
, где

– не существует

Таким образом, не существует передаточной функции идеального квантователя

Предположим, что дальше стоит фильтра низких частот, тогда с очень большой натяжкой

Передаточная функция АЦП , но практически ее не существует.

Ц

ЦАП держит сигнал

АП. Нужно поставить НЧ-фильтр с идеальной прямоугольной частотной характеристикой. Если через него пропустить сигнал, то останется только центральная часть . В ТУ такой фильтр называется экстраполятором. Экстраполятор 0-го порядка.

На выходе разрывная функция

Функция должна держать импульс, поданный на вход, весь период дискретизации.

На выходе получается кусочно-непрерывный сигнал с разрывами 1-го порядка, но он является аналоговым. На вход подается единичная δ-функция.

2. Передаточные функции дискретно-непрерывных устройств управления.

Вычисление передаточной функции W*(s)

x*(t) = x(t) u*(t)

u*(t) = (0) + (t-T) + (t-2T) + ... = (t-kT) – последовательность -функций

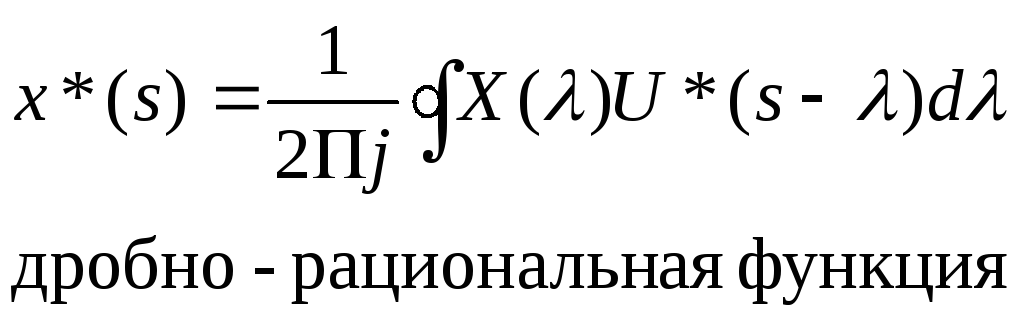
X*(s) = L[ x*(t) ]

U*(s) = L[ u*(t) ]

X(s) = L[ x(t) ]

- осуществляем преобр. в пространство изображений

- подставляем вместо s (s – λ)

Функция дробно-рациональная – можно использовать теорию вычетов

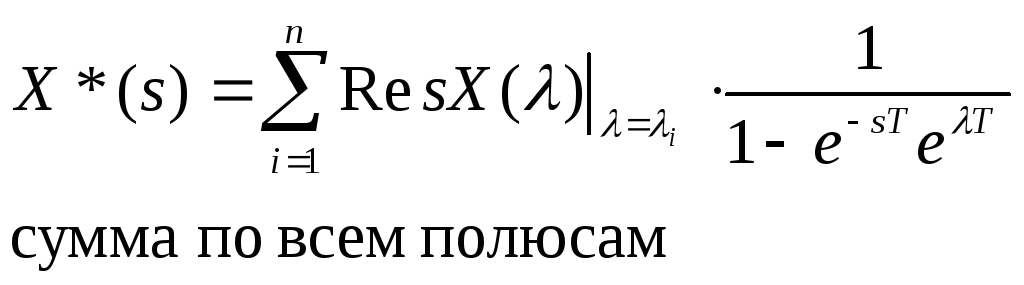
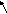
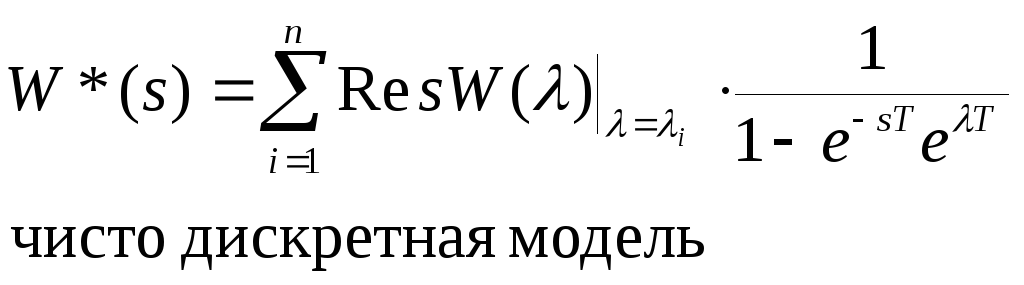
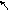
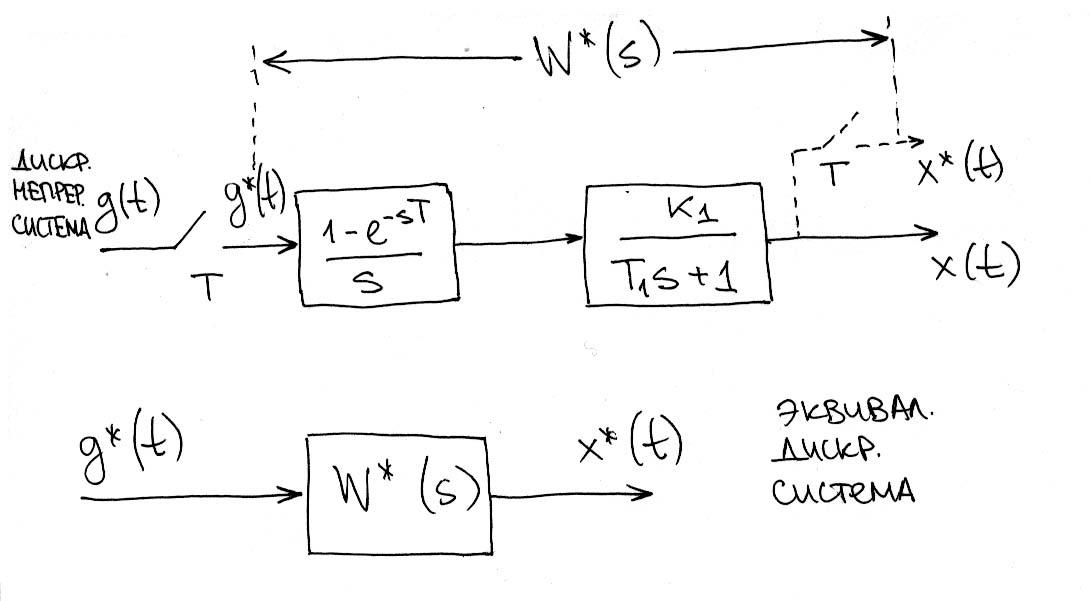
Осуществим расчет дискретной передаточной функции:

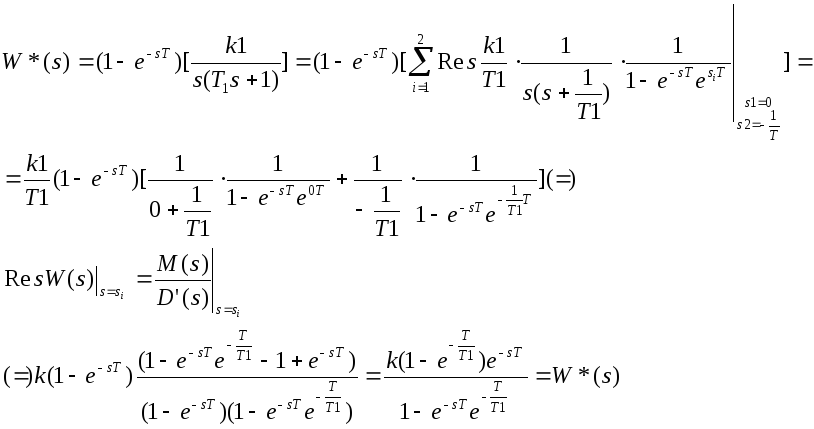
1 + W*(s) = 0 – можем исследовать устойчивость

Алгебраический (в замкнутом состоянии) или частотный (в замкнутом состоянии, на ЛАФЧХ в разомкнутом) критерий.

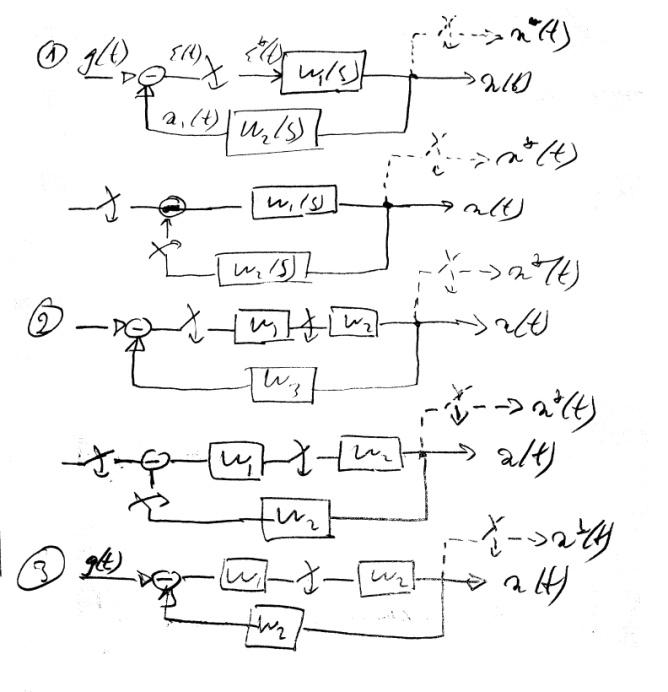
4.Структурные преобразования днс

1. E^*(s)=G^*(s)-X₁^*(s), X₁(s)= E^*(s)W₁(s)W₂(s),

X₁^*(s)= E^*(s)[W₁(s)W₂(s)]^*= E^*(s)W₁W₂^*(s)

X^*(s)= E^*(s)W₁^*(s)

Ф*(s)=X*(s)/G*(s)

2. E^*(s)=G^*(s)-X₁^*(s),

X₁^*(s) = E^*(s)W₁^*(s)W₂W₃^*(s),

3)

ПФ = не существует