8.Функция спектральной плотности мощности сигналов. Оценивание функции спектральной плотности мощности для стационарных эргодических сигналов.

Функция спектральной плотности мощности сигналов

Теорема Парсеваля Теорема Парсеваля позволяет устанавливать величину полной энергии комплексных сигналов с помощью интегрирования либо во временной, либо в частотной областях.

(4.3.5)

Равенство (4.3.5) представляет собой формулировку теоремы Парсеваля и позволяет вычислять полную энергию сигнала как во времен­ной, так и в частотной областях.

Прямое и обратное ДПФ может служить дискретным аналогом прямого и обратного непрерывного преобразования Фурье. Разберём вывод дискретного аналога теоремы Парсева­ля.

Запишем обратное и сопряжённое обратное ДПФ для дискретных значений сигнала :

Образуем произведения просуммируем их поi, изменим порядок суммирова­ния и получим

(4.3.6)

На основе (4.3.6) сформируем выражение, которое является дискретным аналогом теоремы Парсеваля:

(4.3.7)

Определение функции спектральной плотности мощности (СПМ) сигналов связано с аналогией из электротехники – вычислении мощности, выделяемой на активном сопротивлении (см. разд. 2.2).

Применим теорему Парсеваля (4.3.5) для нахождения величины энергии сигнала приходящейся на узкий интервал частот:

Для функции спектральной плотности мощности для стационарного эргодического сигнала в непрерывном случае сформируемотношение части мощности сигнала в частотном диапазоне к величинеДля этого рассмотрим прямое и комплексно-сопряжённое прямое преобразование Фурье для сигналана интервале временикоторые представляются интегралами

(4.3.8)

Энергия сигнала длительностьюв частотном диапазонеможет быть найдена на основе интегралов (4.3.8)

Функция СПМ для рассматриваемого стационарного эргодического сигнала запишется в виде предела, в предположении, что этот предел существует:

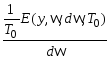
,(4.3.9)

Функция в общем случае определена во всём частотном диапазоне и является положительной 0.

{Рассмотрим обобщение определения функции СПМ сигналов (4.3.9) для дискретного случая. Пусть задаётся набор дискретных значений сигнала T– интервал дискретизации. Интегралы Фурье из (4.3.8) могут быть заменены дискретными суммами, которые являются фактически оценками указанных интегралов для заданной частотыи и с учётом:

.

Нетрудно видеть, что оценки интегралов Фурье сформированы в виде ДПФ. Поэтому – оценка функции СПМ дискретизованного сигнала для фиксированных частот– может быть вычислена через коэффициенты ДПФ:

(4.3.10)}

последовательность технологических этапов получения оценок функции СПМ для стационарных эргодических сигналов,наблюдаемых на большом интервале времениБудем полагать, что обрабатываемые сигналызадаются в непрерывной форме, например в виде записей на аналоговом магнитофоне.

Этап 1. Выбор частоты дискретизации.Пусть– верхнее значение частоты полосы сигнала. (должна быть известной из априорных сведений о сигнале; Согласно теореме Котельникова, частоту дискретизацииследует выбирать, исходя из неравенстваГц;На практикеЕсли в обрабатываемом сигнале доминирует синусоидальная составляющая с частотой, то на период синусоидыдолжно приходитьсяточек дискретизации. Общее число дискретизванных значений сигнала равняется величинеОбъём памяти ЭВМ (ДЗУ), который займут введённые дискретизованные сигналы, в случае, если на одно дискретное значение сигнала отводится 4 байта, составитКбайт. При вводе дискретных данных в ЭВМ следует учитывать ограничение памяти ДЗУ ЭВМ– должно выполняться неравенство.

Этап 2.Выбор параметров локальных интервалов.ЕслиN– выбранное число точек на локальном интервале,m– число локальных интервалов, то должно выполняться условиеНеобходимо выбор параметров локальных интервалов осуществлять таким образом, чтобы числаN,mбыли целыми. Длина локального временного интервалаNTподбирается, исходя из обеспечения требуемой разрешающей способности ДПФf. Для этой цели должна быть определена минимальная разность частот двух соседних частотных составляющихв обрабатываемом многочастотном сигнале. Величиныfидля обеспечения разрешения связаны неравенством,

{Для улучшения разрешения, естественно, следует назначать длинные локальные интервалы. Однако при обеспечении хорошего усреднения результатов цифровой обработки требуется увеличивать – реализовывать большое количество локальных интервалов и тем самым уменьшать длины локальных интервалов. Требования удовлетворительного усреднения и хорошей разрешающей способности являются противоречивыми. Выбор параметровсвязан с принятием компромисса.}

Этап 3. Умножение сигналов на локальных интервалах на функцию временного окна.Пусть для дискретизованного сигналаисходный большой интервал времени разбивается наmлокальных интервалов поNточек. Дискретизованный сигнал наj-м локальном интервале имеет видДля каждого локального интервала осуществляется умножение части дискретизованного сигнала наN‑ точечное временное окно

Этап 4. Вычисление локальных ДПФ и локальных оценок функции СПМ.Нахождение локальных коэффициентов ДПФ {производится в соответствии с формулой ДПФ}

Локальные оценки функции СПМ {находятся с использованием локальных коэффициентов ДПФ}

Этап 5.Вычисление оценок функции СПМ..Усреднение обеспечивает снижение шумовых порешностей в оценке функций СПМ сигналов