6.Стационарные и эргодические сигналы. Оценка моментных характеристик для стационарных эргодических сигналов.

Стационарность случайных cигналов подразумевает неизмен­ность их статистических характеристик во времени. Случайный сигнал называется стационарным в узком смысле, если его n-мерные функции закона распределения вероятностей для группы переменных сдвинутых на время, совпадают и, таким образом, не зависят от времени сдвига

Случайный сигнал является стационарным в широком смысле, если его математическое ожидание и дисперсия не зависят от времени – а его корреляционная (ковариаци­он­ная) функция зависит от разности аргументов –

Стационарный сигнал является эргодическим, если нахожде­ние его статистических характеристик может быть осуществлено усреднением по одной реализации с помощью интегриро­вания на конечном временном интервале длительностьюс последу­ющим предельным переходом:

При дискретизации единственной реализа­ции случай­ного стационарного эргодического сигнала N – число наблюдений сигнала, возмож­на запись оценок математического ожидания и дисперсии в следующем виде:

Оценка корреляционной функции представится как функция дискретного аргумен­та m, :

? для больших mбудет малое число соединений след-но большие погрешности.R_yy⁰(m) неравномерна по точности, когдаmмаленькое суммируется много членов, а когда большоеN-m-1 будет маленькое и точность будет меньше, чем при маленькомm

7.Дискретное преобразование Фурье для действительного и комплексного случаев.

Действительный случай. -наблюдения действительного дискретизованного сигнала, N – число наблюдений, T – интервал дискрети­зации. В самом общем случае для ДПФ не выдвигается никаких специальных требований к наблюдениям сигнала.

Полигармоническую модель с фиксированными частотами для ДПФ в действительном случае

(4.1.4)

Вектор параметров модели и размерность

функционал : (4.1.5)

Оценки параметров для модели (4.1.4) находятся из решения задачи минимизации функционала

Для модели введём векторную базисную функцию размерности:

векторная базисная функция не зависит от интервала дискрети­зации T:

Модель и функционал в скалярном виде: (4.1.7)

Введем на основе материалов разд. 2.4 векторно-матричные обозначения для вектора наблюдений Y размерности вектора параметровразмерностии матрицы плана сигналаX размерности :

, ,

где

Рассмотрим скалярные произведения синусоидальных базисных функций Благодаря предложенному расположению частот в модели введённые базисные функции являются ортогональными

произведения базисных функций для разных индексов

для

Вследствие ортогональности введённых синусоидальных базисных функций матрица размерностиявляется диагональной:

, .

Вектор коэффициентов Фурье размерностипредставляет собой набор скалярных произведений вида

,,…,

Оптимальные параметры модели для ДПФ выразятся через коэффициенты Фурье

(4.1.8)

Основываясь на (4.1.8), запишем формулы, определяющие оптимальные параметры для модели (4.1.4) и являющиеся коэффи­ци­ентами ДПФ для случая действи­тельных наблюдений и действительной модели:

(4.1.9)

{В формулах (4.1.9) опущен знак оптимальности В соответствии с (4.1.9) ДПФ осуществляет линейное преобразование вектора наблюдений сигналаразмерностив вектор параметров моделиразмерности}

Комплексный случай. Пусть – комплексные наблюдения,Введём комплексную модель для наблюдений в точках

– комплексные параметры, W – корень N-й степени из единицы, – комплексные базисные функции,:

Функционал – мера близости комплексных наблюде­ний и модели, запишется с помощью суммы комплексно-сопряженных сомножителей

.(4.1.10)

Введём комплексные векторно-матричные переменные – вектор ком­плек­сных наблюде­ний Y размер­ности (N, 1), вектор комплек­сных параметров модели размер­ности (N, 1) и комплексную матрицу плана сигнала X размер­ности (N, N):

, ,_.

оптимальные оценки параметров

Матрица и вектор коэффи­циентов Фурьевыразятся с использованием комплек­сных сопряже­ний. Коэффициенты ДПФ находят­ся из системы

Базисные комплексные синусоидальные функции ортого­нальны, и поэтому матрицаD диаго­наль­на. Вычис­лим коэффициенты этой матрицы, сформи­ровав тригоно­метрические суммы, являющиеся скаляр­ными произве­дениями для столбцов комплек­сной матрицы плана сигнала:

Для индексов имеемдляследует, чтоТогда нетрудно видеть, что

, ,

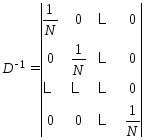Коэффициенты ДПФ для случая комплексных наблюдений и комплексной модели запишутся следующим образом:

,(4.1.11)

где так же, как и в (4.1.9), опущен знак оптимальности.

Вычислим остаточную сумму для оптимальных коэффи­циентов комплексного ДПФ. Подста­вим под знак суммы (4.1.10) получен­ные выражения для коэффициен­тов :



Рассмотрим отдельно выражение в скобках под знаком суммы, переставим порядки суммирования, учитывая, что

для для

Остаточная сумма для функционала (4.1.10) на опти­маль­ных коэффициентах ДПФ равняется нулю – предлагаемая тригонометри­ческая модель с нулевой погрешностью аппрокси­мирует наблюдения. Благодаря этому обстоятельству можно записать формулы прямого и обратного дискретного преобра­зова­ния Фурье, физический смысл которых очевиден

Приведём показа­тельную форму для комплексного ДПФ. Определим амплитуды и фазысоставляющих ДПФ в зависимости от дискретного номераk:

{Результаты вычисления составляющих ДПФ можно графически изображать в виде амплитудного и фазового спектров. Для удобств изображений амплитудных спектров применяется логарифмический масштаб:

Вполне правомерно введение зависимости от частоты для составляющих спектра ДПФ. Шаг дискретности по частоте для составляющих определяется интерва­лом наблюдения NT, Составляющие спектра – амплитуды и фазы модельных комплексных синусоид – распола­гаются равно­мер­но по оси частот,, где так же, как и разд. 4.1.2,}