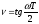- •1. Математическое описание процесса квантования.
- •Передаточные функции аналого-цифровых и цифро-аналоговых преобразователей.
- •Передаточные функции дискретно-непрерывных устройств управления.
- •4.Структурные преобразования днс
- •Основы теории z-преобразования.
- •Методы анализа устойчивости цифровых систем.
- •Применение билинейного преобразования к передаточным функциям разомкнутых систем управления.
- •Построение логарифмических амплитудной и фазовых характеристик, записанных относительно псевдочастоты.
- •9. Синтез последовательного корректирующего устройства в дискретно-непрерывных системах с помощью билинейного преобразования.
- •10.Учёт реального времени в управляющих программах.
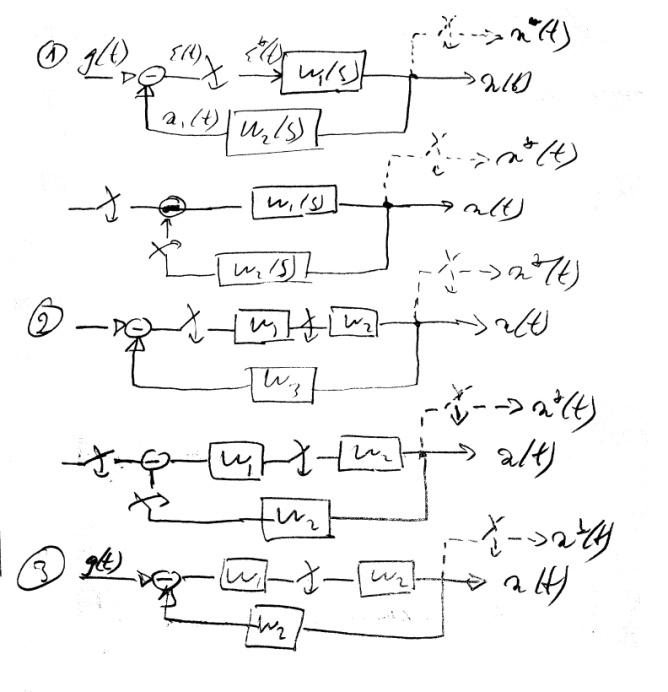
4.Структурные преобразования днс
-
E*(s)=G*(s)-X1*(s), X1(s)= E*(s)W1(s)W2(s),
X1*(s)= E*(s)[W1(s)W2(s)]*= E*(s)W1W2*(s)
X*(s)= E*(s)W1*(s)
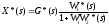
Ф*(s)=X*(s)/G*(s)
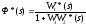
-
E*(s)=G*(s)-X1*(s),
X1*(s) = E*(s)W1*(s)W2W3*(s),
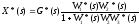
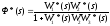
-
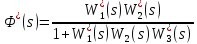 (лучше
не писать, подозрительно)
(лучше
не писать, подозрительно)
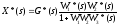
ПФ
=
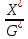 не существует
не существует
-
Основы теории z-преобразования.
Z=esT s=σ+jω, s – комплексная переменная.
ReZ= eTσcosωT ImZ= eTσsinωT
z-преобразование используется только для дискретных по времени сигналов. X(z) – z-преобразование сигнала x*(t), если x(t), то предполагается, что сигнал квантуется по времени.
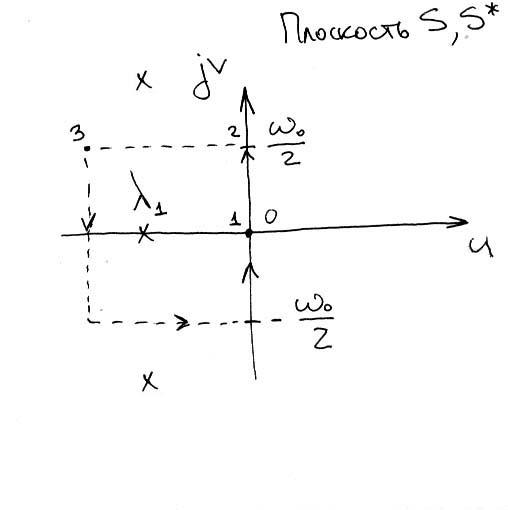
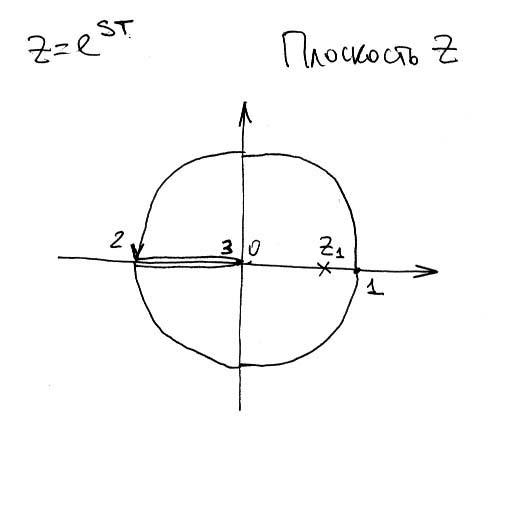
Таким образом основная полоса преобразуется в окружность единичного радиуса. Причем полюса, находящиеся в левой полуплоскости, лежат внутри круга.
Доп. полюса наложатся точно также. Следовательно, вся левая полуплоскость отражается в круг единичного радиуса.
W(s)
3-го порядка, λi
– полюса. W*(s)
-> появляется полоса
 .
Полюса повторяются, так как появляется
трансцендентная модель.
.
Полюса повторяются, так как появляется
трансцендентная модель.
Z=esT s=jω
точки:
1) s=0 2)
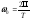 3)
3)
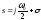 4)
4)
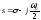
|λi |< 1 для всех полюсов в левой полуплоскости, она находятся внутри окружности. Для 2-й полосы полюсы в z-плоскости получаются те же. Проблема трансцендентности снимается.
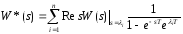
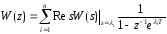
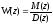 ,
где M(z)
и D(z)
– дробно-рациональные ф-ии
,
где M(z)
и D(z)
– дробно-рациональные ф-ии
Пример
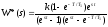

Теоремы z-преобразований:
1)
Теорема о начальном значении:
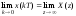 .
Если x(t)
имеет z-преобрахование,
и предел существует, то выполняется
теорема, и начальное значение функции
равно пределу.
.
Если x(t)
имеет z-преобрахование,
и предел существует, то выполняется
теорема, и начальное значение функции
равно пределу.
2)
Теорема о конечном значении: Если
x(t)->X(z)
для любого |zi|
< 1 и если функция (1-z-1)X(z)
не имеет полюсов вне единичной окружности,
то
 .
.
Обратное
z-преобразование:

-
Методы анализа устойчивости цифровых систем.
Замкнутая система
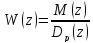
1+W(z)=0 => anzn+an-1zn-1+…+a1z+a0=0
полюса – z1…zn
Система
устойчива
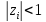 для всех полюсов
для всех полюсов
1) алгебраические критерии.
- критерий Гурвица
- критерий Шур-Кона
Они оперируют с коэффициентами an, an-1, …, a1, a0. По алгебраическим критериям нельзя определить запасы устойчивости.
2) частотные критерии
Критерий Найквиста для дискретного случая остается практически неизменным, за исключением того, что меняется на :
Для того, чтобы ЛДС была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы ее частотные характеристики в разомкнутом состоянии обладали следующими свойствами: число переходов фазовой характеристики через прямую -180 ( -540, … ) при L() > 0 равнялось m/2 (m-число полюсов в правой полуплоскости в разомкнутом состоянии).
Переход сверху–вниз с минусом, снизу-вверх с плюсом
-
Применение билинейного преобразования к передаточным функциям разомкнутых систем управления.
пл. s пл.z пл.w
Вводится
новая плоскость – разворачиваем
окружность единичного радиуса в левую
полуплоскость.
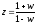
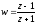
z = ejT = cos(T) + jsinT

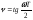
- псевдочастота (безразмерная величина)
– чисто мнимая переменная, окружность
снова разворачивается в левую
полуплоскость.
- псевдочастота (безразмерная величина)
– чисто мнимая переменная, окружность
снова разворачивается в левую
полуплоскость.
Связь псевдочастоты с кр. частотой :
|
|
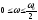
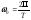

если
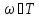 ,
то зависимость линейная
,
то зависимость линейная

При применении сначала z-, а затем w-преобразования к передаточной функции получим W(w). Появятся типовые звенья, но уже от w, а не от s.
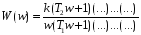 ;
;
s = j w = j
- псевдочастота