6.5. Cинтез ких-фильтров

КИХ-фильтры были определены в разд. 6.1. Эти фильтры задаются набором коэффициентов и реализуют скользящее взвешенное суммирование последовательности входного сигнала Выходной сигнал КИХ-фильтра формируется в соответствии с формулой

(6.5.1)

вычисления начинаются с Передаточная функция для разностного уравнения КИХ-фильтра (6.5.1) записывается в виде

(6.5.2)

Импульсно-переходная функция для (6.5.1) определена в точках,ПФ для КИХ-фильтра (6.5.2) линейно зависит от коэффициентовУказанное обстоятельство приводит к квадратичным функционалам при решении аппроксимационных задач, что позволяет в ряде случаев эффективно реализовывать синтез КИХ-фильтров на основе соответствующих систем линейных уравнений.

6.5.1. Синтез КИХ-фильтров на основе метода аппроксимации

в частотной области

Рассмотрим достаточно общую постановку задачи синтеза КИХ-фильтров на основе метода аппроксимации в частотной области. Пусть на фиксированном частотном диапазоне заданы частотные точкине обязательно расположенные равномерно. В этих точках определены комплексные значения эталонной ПФкоторые необходимо аппроксимировать в точкахс помощью комплексной ПФсинтезируемого КИХ-фильтра. Будем здесь полагать, что коэффициенты являются комплексными.

Представим выражение для ПФ КИХ-фильтра в форме скалярного произведения, введя векторыa и

Сформируем квадратичный по вектору коэффициентов a функционал определяющий близость эталонной ПФ и передаточной функции КИХ-фильтра, которая образуется в результате синтеза

(6.5.3)

Нахождение вектора обеспечивающего синтез КИХ-фильтра, сводится к минимизации функционала (6.5.3). Введём необходимые векторно-матричные обозначения

,

.

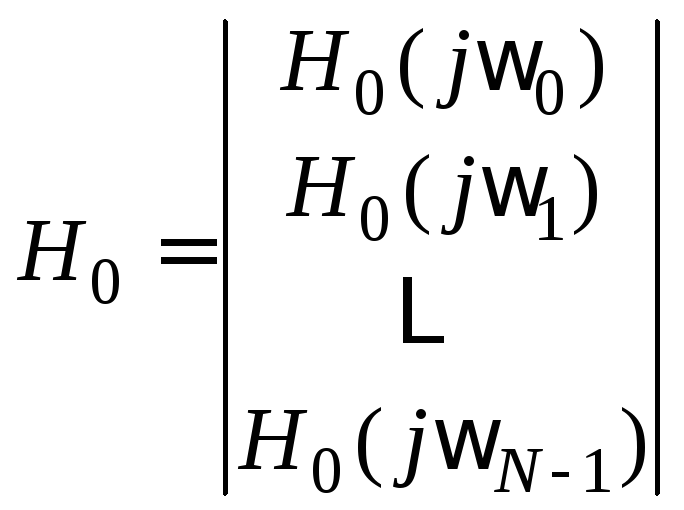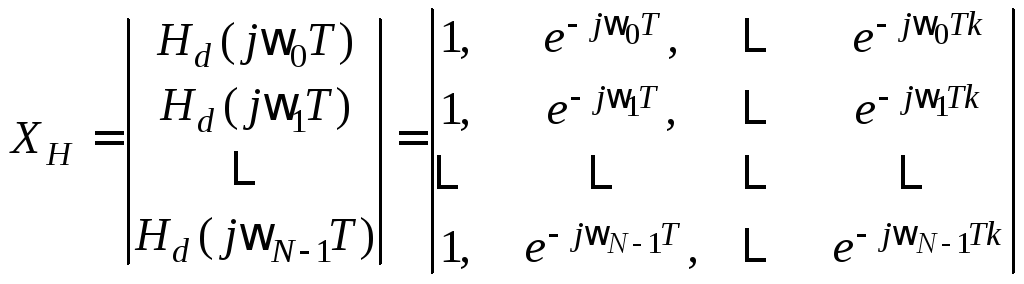Воспользуемся результатами построения линейных моделей разд. 2.4 для комплексного случая (2.4.8), (2.4.11). Вычисление производится на основе решения системы комплексных линейных уравнений

(6.5.4)

В отличие от общей постановки синтеза ЦФ, описанной в разд. 6.3, как аппроксимационной задачи, решаемой на основе нелинейного программирования, изложенный подход синтеза КИХ-фильтра ввиду того, что оптимизируемый функционал является квадратичным, принципиально позволяет решить задачу построения КИХ-фильтров с комплексными коэффициентами с помощью решения соответствующей комплексной системы линейных уравнений размерности(6.5.4).

Необходимо иметь в виду, что предложенный подход решает задачу аппроксимации синтезированной ПФ к эталонной ПФ в точкахОднако при этом остаётся открытым вопрос о поведении синтезированной ПФ для частот , находящихся между частотными точками ,Следует также учитывать, что для большихk и близких частот могут возникать вычислительные проблемы, связанные с решением линейной системы (6.5.4).

6.5.2. КИХ-фильтры с линейными ФЧХ

КИХ-фильтры с линейными ФЧХ используются в многочисленных задачах синтеза. Существуют четыре варианта КИХ-фильтров с линейной ФЧХ, которые обусловлены четырьмя типами симметрии коэффициентов КИХ-фильтров. Запишем выражение для ПФ КИХ-фильтра

Вариант КИХ-фильтра 1. Порядок k – чётное число и для коэффициентов фильтра выполняются равенства обеспечивающие симметриюотносительно коэффициента

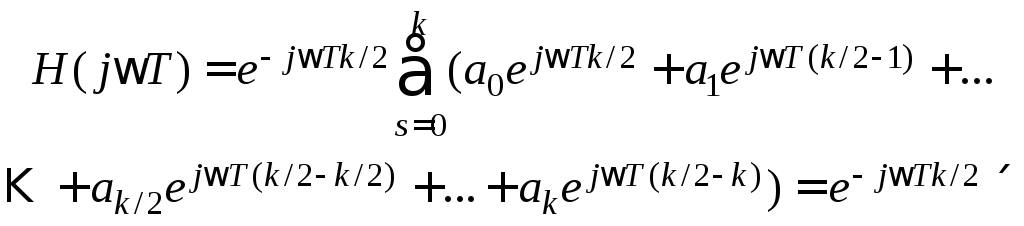
(6.5.5)

ФЧХ для КИХ-фильтра первого вида (6.5.5) представляется линейной функцией частоты

Вариант КИХ-фильтра 2. Порядок k – нечётное число и для коэффициентов фильтра выполняются равенства обеспечивающие симметрию:

. (6.5.6)

Вариант КИХ-фильтра 3. Порядок фильтра k – чётное число и для коэффициентов фильтра выполняются равенства обеспечивающие антисимметрию относительно

(6.5.7)

Вариант КИХ-фильтра 4. Порядок фильтра k – нечётное число и для коэффициентов фильтра выполняются равенства обеспечивающие антисиметрию:

. (6.5.8)

6.5.3. Синтез КИХ-фильтров методом оконных функций

Комплексная ПФ любого ЦФ является периодической функцией частоты с периодом, равным частоте дискретизации Представим эталонную ПФсинтезируемого ЦФ её в виде комплексного ряда Фурье с использованием (2.5.2):

(6.5.9)

где параметры с номерамиs определяются в соответствии с известной формулой для коэффициентов комплексного ряда Фурье (2.5.4):

Нетрудно убедиться из (6.5.9), что коэффициенты разложения ПФ ЦФ в ряд Фурье могут интерпретироваться как отсчёты импульсно-переходной функции Если ввести замену то на основе (6.5.9) можно получить ПФ ЦФ в форме z-преобразования

(6.5.10)

Определённая подобным образом ПФ (6.5.10) описывает физически нереализуемый ЦФ бесконечного порядка.

Для получения ЦФ конечного порядка необходимо провести усечение ряда (6.5.10), полагаяприЗдесь примем для упрощения выкладок, что порядокk является чётным числом. Случай нечётного порядка k производится почти аналогично. Произведём усечение в (6.5.10), получим

(6.5.11)

Физическая реализуемость ЦФ с передаточной функцией типа (6.5.11) может быть достигнута путём умножения из (6.5.11) на

(6.5.12)

Подобная модификация ПФ допустима, поскольку АЧХ при этом остаётся неизменной, а фазовое запаздывание уменьшается на величину Подстановкойв выражение (6.5.12) можно получить комплексную ПФ физически реализуемого ЦФ

Рассмотрим случаи, когда импульсно-переходная характеристика КИХ-фильтра симметрична и антисиметричнаk – чётное число. В первом случае имеем следующее выражение для ПФ КИХ-фильтра:

и во втором случае ПФ КИХ-фильтра имеет вид

Усечение ряда (6.5.10) и формирование ПФ (6.5.12) приводит к эффекту Гиббса, связанному с образованием пульсаций АЧХ около её точки разрыва (точки среза). Использование весовой последовательности конечной длины которая называетсяоконной функцией, для умножения коэффициентов Фурье с целью регулирования сходимости усечённого ряда Фурье даёт хорошие результаты в отношении устранения эффекта Гиббса.

Пусть – частотная функция неусечённого ЦФ из (6.5.10). Положим, что для выбранной оконной функции найдена частотная функция

Обозначим через частотную функцию КИХ-фильтра, полученного в результате умножения коэффициентов импульсно-переходной функции на функцию окна. Произведение функций во временной области переводится в свёртку в частотной области. Тогда очевидна запись в виде свёртки

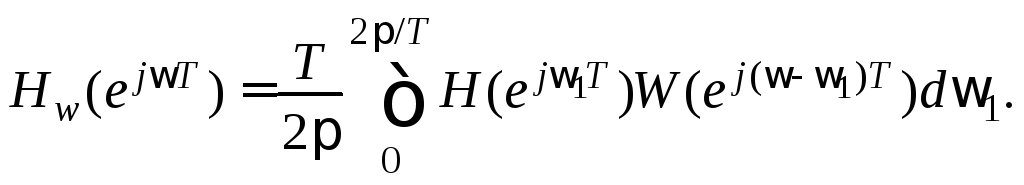
Частотная функция окна должна иметь главный лепесток, содержащий почти всю энергию окна, и боковые лепестки, которые должны обычно быстро затухать. При определённом выборе функции окнаудаётся устранить явление Гиббса. Наиболее часто для рассматриваемой здесь задачи используются временные оконные функции Хэннинга, Хемминга и Блэкмана. Разумеется, существует целый ряд других функций окон.

Рассмотрим пример синтеза низкочастотного КИХ-фильтра с заданными T и заданной эталонной функцией АЧХ в виде

при

при

Будем полагать, что для эталонной ПФ справедливо равенство длядляиимеет период

Найдём импульсно-переходную характеристику предполагаемого к синтезу КИХ-фильтра на основе разложения в ряд Фурье вычислим интеграл в симметричных пределах:

.

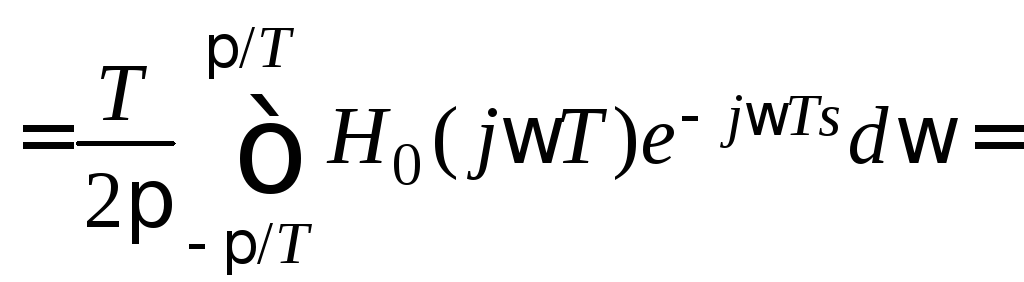
Запишем выражение для ПФ физически реализуемого КИХ-фильтра для z-переменных, пусть k – чётное число:

где

ПФ синтезированного КИХ-фильтра имеет вид

(6.5.13)

КИХ-фильтр (6.5.13) синтезирован с прямоугольным окном припри. На рис. 6.5.1а, 6.5.1б изображены АЧХ исинтезированного КИХ-фильтра (6.5.13) дляв линейном и логарифмическом масштабе. Видно, что в окрестности частоты срезафункция АЧХ имеет значительные пульсации в полосе пропускания и задерживания.

Рис. 6.5.1а. АЧХ синтезированного КИХ-фильтра с прямоугольным окном

в линейном масштабе

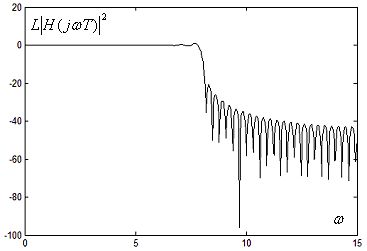
Рис. 6.5.1б. АЧХ синтезированного КИХ-фильтра с прямоугольным окном

в логарифмическом масштабе

Этот же пример рассмотрим, когда для синтеза КИХ-фильтра используется окно Хэннинга. Для этого последовательность коэффициентов умножается на функциюкоторая описывается весовой функцией

при при

Модифицированная ПФ для синтезированного фильтра представляется формулой

(6.5.14)

На рис. 6.5.2а, 6.5.2б изображены АЧХ синтезированного КИХ-фильтра с окном Хэннинга в линейном и логарифмическом масштабе. Видно, что благодаря применению окна существенно снижаются пульсации в полосе пропускания и уровень пульсаций в полосе задержания снижается почти до 50 Дб.

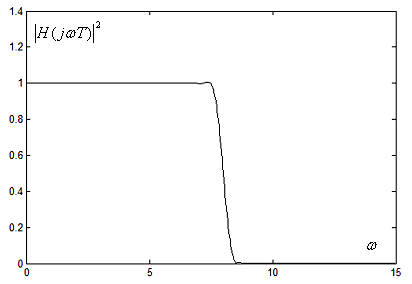
Рис. 6.5.2а. АЧХ синтезированного КИХ-фильтра с окном Хэннинга

в линейном масштабе

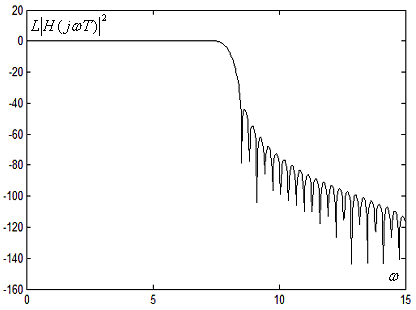
Рис. 6.5.2б. АЧХ синтезированного КИХ-фильтра с окном Хэннинга

в логарифмическом масштабе

Рис. 6.5.3а. АЧХ синтезированного КИХ-фильтра с окном Блэкмана

в линейном масштабе

Рис. 6.5.3б. АЧХ синтезированного КИХ-фильтра с окном Блэкмана

в логарифмическом масштабе

Рассмотрим пример синтеза КИХ-фильтра с использованием окна Блэкманна

при

при

ПФ для синтезированного КИХ-фильтра с представляется формулой

. (6.5.15)

Из рис. 6.5.3а и 6.5.3б видно, что в результате применения окна Блэкмана практически полностью устраняются пульсации в полосе пропускания и уровень пульсаций в полосе задерживания снижается до 80 Дб.

6.5.4. Синтез КИХ-фильтров методом частотных выборок

Продолжим рассмотрение задачи построения КИХ-фильтров в частотной области. Передаточная функция КИХ-фильтров внешне напоминает дискретное преобразование Фурье. Воспользуемся этим обстоятельством при решении задачи синтеза. Действительно, запишем снова выражение ПФ

Расположим частотные точки равномерно Пусть комплексные значениязадают эталонную ПФ для КИХ-фильтра в равномерно расположенных дискретных частотных точках. Введём нормированные частотные выборкиОчевидно, что последовательности частотных выбороки коэффициентысвязаны прямым и обратным дискретным преобразованием Фурье:

На практике решение задачи синтеза КИХ-фильтров практически всегда связано с тем, что требуется синтезировать АЧХ заданного вида с помощью КИХ-фильтра с действительными коэффициентами Воспользуемся подходом разд. 6.5.2, основанным на формировании КИХ-фильтров с линейными ФЧХ.

Рассмотрим пример задачи синтеза с k-нечётным. Сформируем симметричную АЧХ которая соответствует в точкахзначениям заданной эталоннойТогда коэффициенты КИХ-фильтра представятся следующей формулой:

Нетрудно видеть, что симметричные коэффициенты являются действительными.

6.5.5. Синтез КИХ-фильтров по методу аппроксимации

во временной области

Данный метод синтеза основан на решении задачи аппроксимации во временной области наблюдений сигнала на ограниченном числе дискретных точек с помощью линейной по параметрам модели. Рассмотрим с учётом определённых допущений используемую здесь задачу аппроксимации и предлагаемый алгоритм синтеза.

Пусть задана выборка из наблюдений сигналаАппроксимируем указанные наблюдения линейной по параметраммоделью в виде полиномиальной функции

Cформируем квадратичный функционал

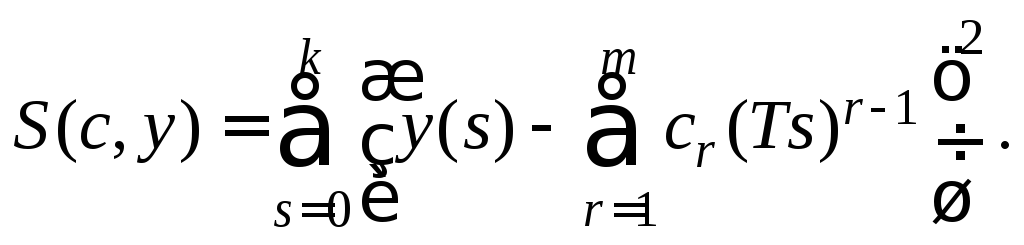
Решение задачи аппроксимации связано с вычислением оптимального вектора параметров модели, который обеспечивает минимальное значение функционала, физический смысл которого очевиден. С помощью векторно-матричных обозначений вектора наблюденийи матрицыоптимальный вектор параметровнаходится следующим образом:

, ,

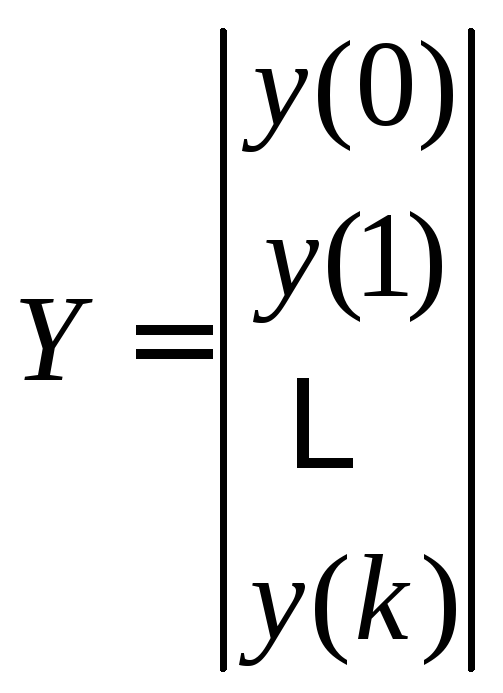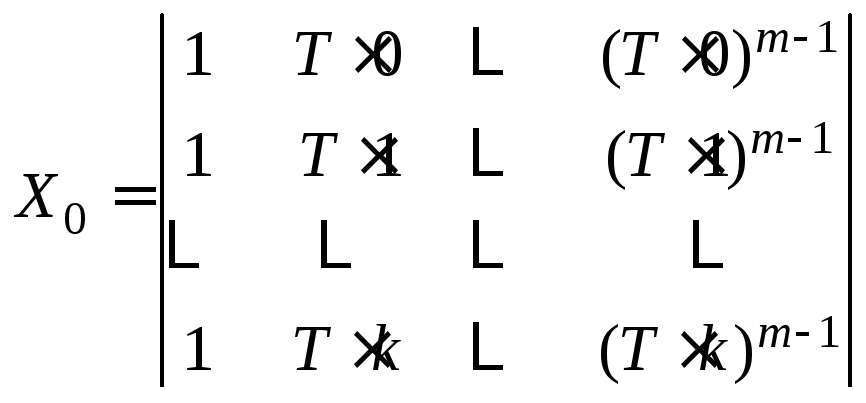Для того, чтобы избежать проблем с вычислениями, будем полагать, что принимают малые значения.

Введём матрицу D размерности и представим векторв виде линейной функции от вектора наблюдений

(6.5.16)

где – коэффициенты матрицыD. Модель сигнала для вектора параметров в некоторой точкеi, может быть найдена в виде линейной комбинации наблюдений

Точка i в общем случае не связана со значением k; рассмотрим частный случай Введём коэффициентыи представим значение модели сигнала в точкеk в виде свёртки

(6.5.17)

Примем в качестве результата фильтрации наблюденийдля точкиk, введём обозначение

, (6.5.18)

Основываясь на выражении (6.5.18), можно сформировать КИХ-фильтр. Положим, что последовательность наблюдений сигнала реализована дляРезультат фильтрации сигналав точкеi, полученный на основе скользящего усреднения наблюдений дляпредставляется соотношением

. (6.5.19)

Алгоритм синтеза КИХ-фильтра во временной области базируется на соотношении (6.5.16), которое позволяет вычислить по коэффициентыматрицыD, и соотношении (6.5.17), на основе которого может быть вычислен вектор (или

Разберём пример синтеза КИХ-фильтра во временной области по трём наблюдениям которые соответствуютВ качестве аппроксимационной модели выбираем прямую линиюВведём векторно-матрич­ные обозначения и произведём необходимые вычисления, положивОпустив промежуточные выкладки, получим

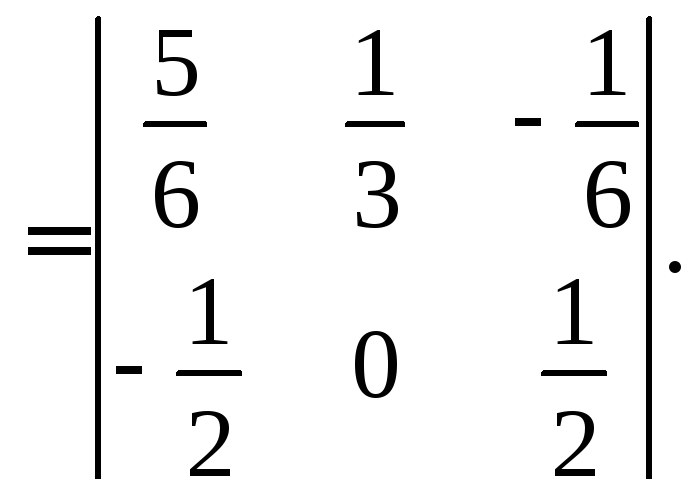
Оптимальные коэффициенты модели примут вид

Значение модели в точке представится следующим образом:

(6.5.20)

Уравнение КИХ-фильтра, реализующего скользящее усреднение, и его коэффициенты запишутся на основании (6.1.20):

(6.5.21)

На рис. 6.5.4 представлены результаты математического моделирования работы КИХ-фильтра, синтезированного по предлагаемому алгоритму. Модельные зашумленные наблюдения сформируются по формуле

(6.5.22)

где – модельные случайные нормальные числа с нулевым математическим ожиданием и дисперсией Для (6.5.22) приняты численные значения параметровВ качестве модельной функции, реализующей аппроксимацию наблюдений, взята прямаяУравнение КИХ-фильтра представится следующей формулой:

где – значения его вычисленных по (6.5.16) и (6.5.17) коэффициентов.

Пунктирная кривая 1 относится к исходному экспоненциальному сигналу ломаная линия2 с крестиками соответствует зашумлённым наблюдениям ломаная линия с кружочками обозначает выходной сигнал фильтраВычисленияреализованы для точекна кривой3 принято дляАнализ кривых на рис. 6.5.4 позволяет сделать вывод, что описанный метод синтеза КИХ-фильтров на основе аппроксимации во временной области является вполне работоспособным.

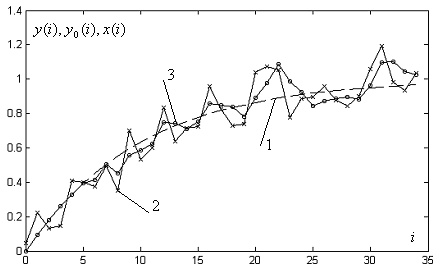
Рис. 6.5.4. Результаты математического моделирования работы

КИХ-фильтра, синтезированного по методу аппроксимации

во временной области

Список вопросов для самопроверки к гл. 6

1. В чём состоит определение для разностных уравнений ЦФ?

2. Могут ли быть определены импульсно-переходные функции для нелинейных ЦФ?

3. В чём состоит физический смысл определения передаточных функций ЦФ?

4. Влияет на характер устойчивости ЦФ расположение на комплексной плоскости его нулей?

5. Какие этапы можно определить при решении задачи синтеза ЦФ на основе аппроксимации?

6. Какие этапы можно определить при решении задачи синтеза ЦФ на основе билинейного преобразования?

7. В чём состоят постановка и основные этапы задачи синтеза ЦФ Баттерворта?

8. В чём состоят постановка и основные этапы задачи синтеза КИХ-фильтров с помощью оптимизации в частотной области?

9. В чём состоят постановка и основные этапы задачи синтеза КИХ-фильтров с использованием ДПФ?

Список задач к гл. 6

1. Основные формулы для цифровых фильтров

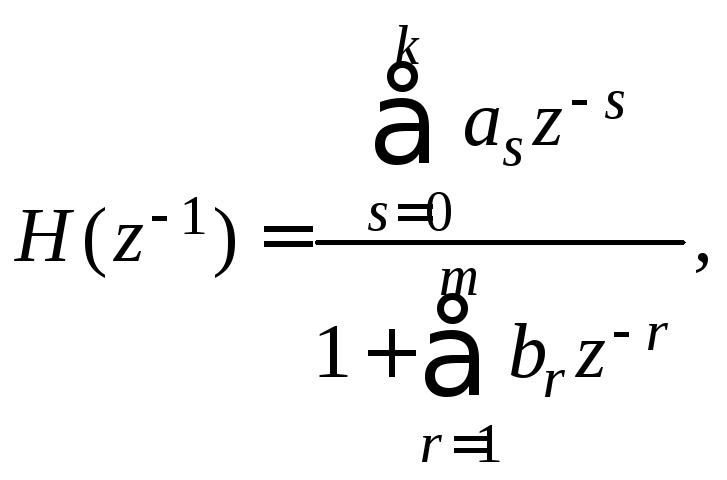
2. Записать выражение для передаточной функции ЦФ, основываясь на разностных уравнениях:

2)

3)

4)

3. Записать выражение для разностных уравнений ЦФ, заданных передаточными функциями:

1)

2)

3)

4)

5)

4. Построить АЧХ для ЦФ, заданных разностными уравнениями:

1)

2)

3)

4)

5)

6)

7)

8)

СПИСОК ЛИТЕРАТУРЫ

1. Айчифер Э.С., Джервис Б.У. Цифровая обработка сигналов: практический подход. М.: Издательский дом «Вильямс», 2004. 992 с.

2. Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для вузов. М.: Высшая школа, 2000. 448 с.

3. Бендат Дж., Пирсол А. Прикладной анализ случайных данных: пер. с англ. М.: Мир, 1989. 540 с.

4. Бендат Дж., Пирсол А. Применение корреляционного и спектрального анализа: пер. с англ. М.: Мир, 1983. 312 с.

5. Васильев В.П., Муро Э.Л., Смольский С.М. Основы теории и расчёта цифровых фильтров. М.: ACADEMIA, 2007. 272 с.

6. Введение в цифровую фильтрацию / Под. ред. Р. Богнера и А. Константинидиса. М.: Мир, 1982. 216 с.

7. Гадзиковский В.И. Теоретические основы цифровой обработки сигналов. М.: Радио и связь, 2004. 344 с.

8. Гадзиковский В.И. Методы проектирования цифровых фильтров. М.: Горячая линия-Телеком, 2007. 416 с.

9. Гетманов В.Г. Цифровая обработка сигналов. М.: МИФИ, 1997. 128 с.

10. Голд Б., Рейдер Ч. Цифровая обработка сигналов. М.: Сов. радио, 1973. 368 с.

11. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. М.: Радио и связь, 1990. 224 с.

12. Гоноровский И.С., Дёмин М.П. Радиотехнические цепи и сигналы. Учебник для вузов. М.: Радио и связь, 1994. 512 с.

13. Каппелини В., Константинидис А. Дж., Эмилиани П. Цифровые фильтры и их применение. М.: Энергоатомиздат, 1983. 360 с.

14. Лайонс Р. Цифровая обработка сигналов. М.: ООО «Бином-Пресс», 2006. 656 с.

15. Лэй Э. Цифровая обработка сигналов для инженеров и технических специалистов. М.: ООО «Группа ИДТ», 2007. 336 с.

16. Макс Ж. Методы и техника обработки сигналов при физических измерениях. В 2-х т. М.: Мир, 1983. Т.1. 251 с.; Т.2. 256 с.

17. Оппенгеймер А., Шафер Р. Цифровая обработка сигналов. М.: Техносфера, 2007. 856 с.

18. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. М.: Мир, 1982. 428 с.

19. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. М.: Мир, 1978. 848 с.

20. Сергиенко А.Б. Цифровая обработка сигналов. СПб.: Питер, 2002. 608 с.

21. Сиберт У.М. Цепи, сигналы, системы. В 2-х ч.: пер. с англ. М.: Мир, 1988.

22. Смит С. Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников. М.: Изд-во Додэка ХХI, 2008. 720 с.

23. Солонина А.И., Улахович Д.А., Арбузов С.М., Соловьёва Е.Б. Основы цифровой обработки сигналов. СПб.: БХВ-Петербург, 2005. 768 с.

24. Тьюки Дж. Анализ результатов наблюдения. М.: Мир, 1981. 567 с.

25. Умняшкин С.В. Теоретические основы цифровой обработки и представления сигналов: Учебное пособие. М.: Инфра-М Форум, 2009. 304 с.

26. Хемминг Р.В. Цифровые фильтры / пер. с англ.; ред. пер. О.А. Потапов. М.: Недра, 1987. 221 с.

27. Химмельблау Д. Анализ процессов статистическими методами. М.: Мир, 1973. 959 с.

Виктор Григорьевич Гетманов

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ

Издание 2-е, расширенное и переработанное

Редактор М.В. Макарова

Компьютерная верстка С.В. Тялиной

Подписано в печать 28.07.2010 г. Формат 6084 1/16.

Уч.-изд. л. 14,5. Печ. л. 14,5. Тираж 000 экз. Изд. № 042-1. Заказ № 000

Национальный исследовательский ядерный университет «МИФИ».