6.2. Передаточные функции и условие устойчивости для цф

6.2.1. Передаточные функции для ЦФ

Передаточные функции (ПФ) для ЦФ определяются его выходным сигналом в установившемся режиме при действии на входе фильтра единичного дискретного комплексного синусоидального сигнала

где T – интервал дискретизации, частота входного сигнала – В установившемся режиме выходной сигнал ЦФ представляет собой комплексную синусоидальную функцию с частотой входной синусоиды и отличающуюся от входной синусоиды амплитудными и фазовыми искажениями, которые зависят от частоты. Проиллюстрируем этот факт с помощью математического моделирования. Рассмотрим ЦФ первого порядка в виде цифрового апериодического звена (6.1.3) со входным сигналом в виде синусоиды

(6.2.1)

Для расчётов брались значения параметров фильтра начальное условиеНа рис. 6.2.1 пунктирной линией изображён вычисленный входной синусоидальный сигналвремя наблюдения составляет величинусплошной линией изображён вычисленный выходной сигнал ЦФ

Видно, что после непродолжительного переходного процесса наступает установившийся режим – на выходе ЦФ формируется установившийся синусоидальный сигнал с частотой входного сигнала и с амплитудными и фазовыми искажениями. Из анализа графика выходного сигнала можно сделать приближённые оценки для искажённой амплитуды, которая равняетсяи фазового запаздывания, равного

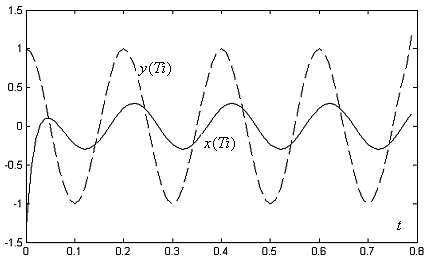
Рис. 6.2.1. Моделирование установившегося режима для ЦФ

Введём комплексный коэффициент не зависящий от дискретного индексаi и позволяющий связать входной и выходнойкомплексные синусоидальные сигналыв установившемся режиме:

Коэффициент по определению является передаточной функцией. Отметим, что ПФ является комплексной функцией частоты и может быть представлено в показательной форме

где – амплитудно-частотная характеристика (АЧХ) для ЦФ; – его фазочастотная характеристика (ФЧХ).

Произведём вычисления для сдвинутых комплексных синусоид

Подставив эти выражения в разностное уравнение для ЦФ, получим формулу для передаточной функции ЦФ

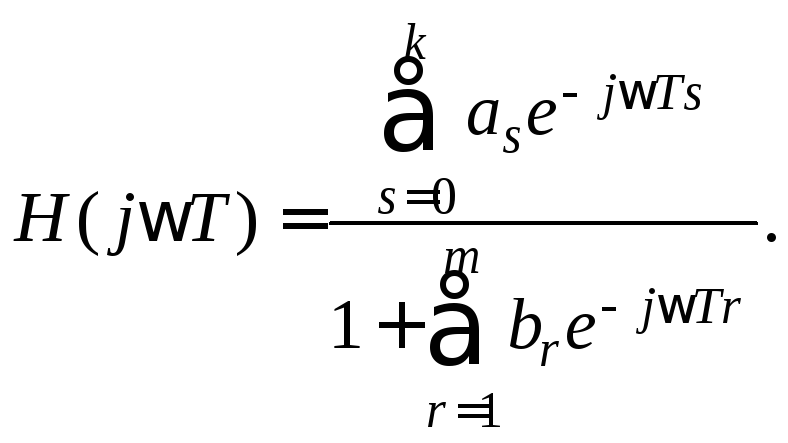(6.2.2)

АЧХ и ФЧХ, которые вычисляются на основе ПФ (6.2.2), позволяют определить амплитудные и фазовые искажения для выходного синусоидального сигнала.

Любому разностному уравнению ЦФ вида (6.1.1) может быть поставлена в соответствие передаточная функция вида (6.2.2). К примеру, для разностного уравнения

передаточная функция для фиксированного значения интервала дискретизации T будет иметь вид

Приведём выражения передаточных функций для ЦФ первого и второго порядка вида (6.1.3), (6.1.4)

(6.2.3)

Очевидно, ПФ является периодической функцией частоты с периодом В самом деле

Для действительных параметров ЦФ ,АЧХ симметрична относительно частоты НайквистаПредставим ПФ в виде суммы косинусных и синусных членов, положим

.

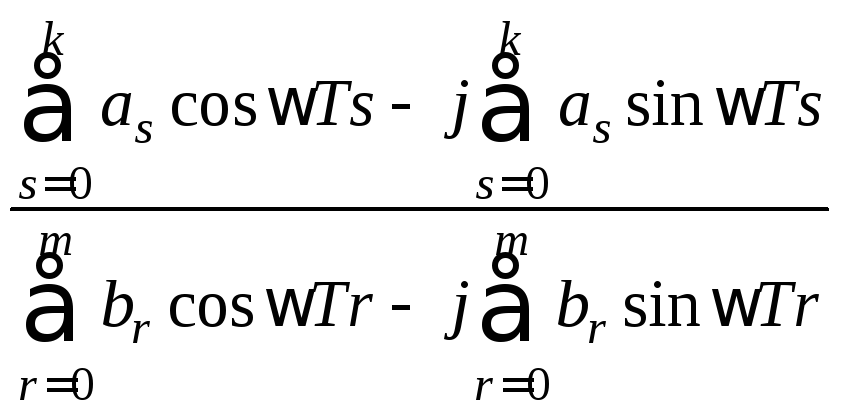Рассмотрим частоты, симметричные относительно Заметим, что

Введём функции частоты для действительной и мнимой части числителя ПФ,– для действительной и мнимой части знаменателя ПФ. С учётом того, что все параметры являются действительными, получим следующие соотношения

Из последнего равенства вытекает свойство симметрии АЧХ (ФЧХ)

Как следует из свойств периодичности, ПФ имеет смысл рассматривать для частотного диапазона, удовлетворяющего неравенству Иногда целесообразно введение нормированной частотыи определение ПФв виде функции введённой нормированной частоты с учётом ограниченияДля действительных параметров ПФ можно ограничиться диапазономВ том случае, если значения АЧХ изменяются в широких пределах, удобно для графических рассмотрений применять логарифмический масштабИзменение АЧХв десять раз соответствует изменениям АЧХ в логарифмическом масштабе на 20 Дб. Пользуясь таким масштабом, на одном графике можно изобразить значения АЧХ для большого динамического диапазона по амплитуде.

Вычислим АЧХ и ФЧХдля цифрового апериодического звена, сделав необходимые преобразования в (6.2.3):

(6.2.4)

На рис. 6.2.2 представлено изображение АЧХ и ФЧХиз (6.2.4) для нормированной частотыw в диапазоне Параметры ЦФ принимали значения Действительный полюс данного ЦФ располагается на правой полуоси.

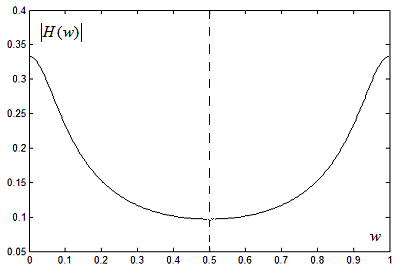
Рис. 6.2.2а. АЧХ для цифрового апериодического звена

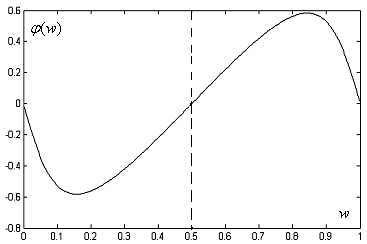
Рис. 6.2.2б. ФЧХ для цифрового апериодического звена

Видно, что АЧХ симметрична и ФЧХ антисимметрична относительно Оценка амплитудного искажения может быть оценена на основе рис. 6.2.2а; дляи частоте Найквиставычислим нормированную частотуиОценка фазового запаздывания определяется из рис. 6.2.2б –

Многие практические задачи, связанные с анализом и построением ЦФ, решаются с помощью представлений ПФ на комплексной плоскости. Вводится переменная с обозначением которая представляет собой при фиксированной частоте некоторую точку единичной окружности на комплексной плоскости. Тогда запишем ПФ как функцию отношения полиномов от введённых переменных

(6.2.5)

где комплексные числа являются нулями; – полюсами ПФ; может трактоваться как комплексный коэффициент усиления.

Крайне полезно для задач ЦОС рассмотреть геометрическую интерпретацию ПФ. На рис. 6.2.3 изображена единичная окружность на комплексной плоскости. Угол задаёт положение переменнойz на единичной окружности – точку O, стрелкой обозначено направление положительного вращения. Точки с кружками соответствуют обозначению нулей ПФ звёздочки обозначают положение полюсовМодуличислителя ПФопределяются длинами векторовсоединяющих точкуO с нулями Аналогичным образом вводятся модули векторовзнаменателя ПФ, которые определяются длинами векторовсоединяющих точку O с полюсами Углыопределяют угловой наклон векторови

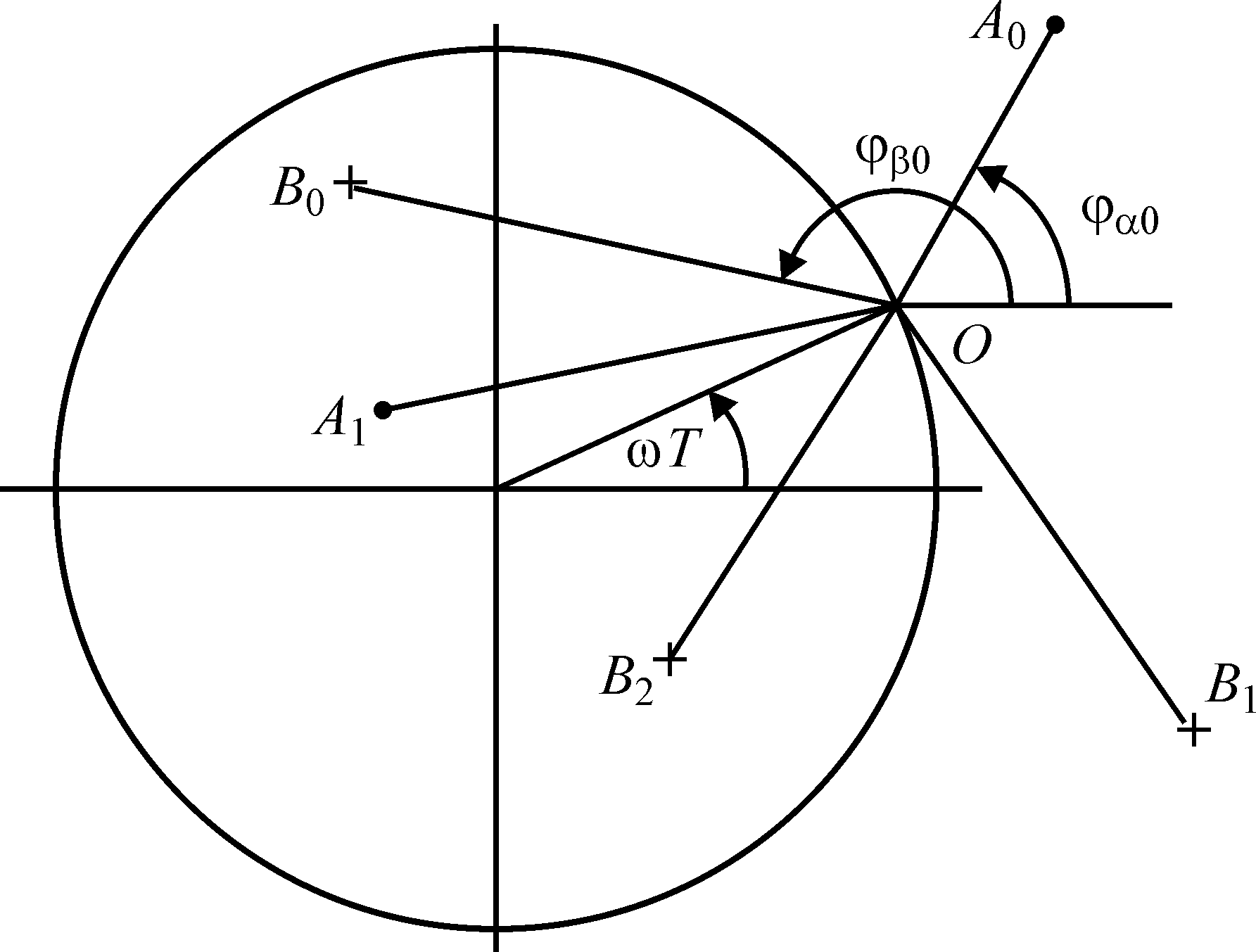
Рис.6.2.3. Геометрическая интерпретация ПФ на комплексной плоскости

Модуль ПФ АЧХ представится как отношение произведений длин указанных векторов. ФЧХ для ЦФ, исходя из геометрической картины рис. 6.2.3, определится соответствующей угловой суммой для уголзадаётся параметром

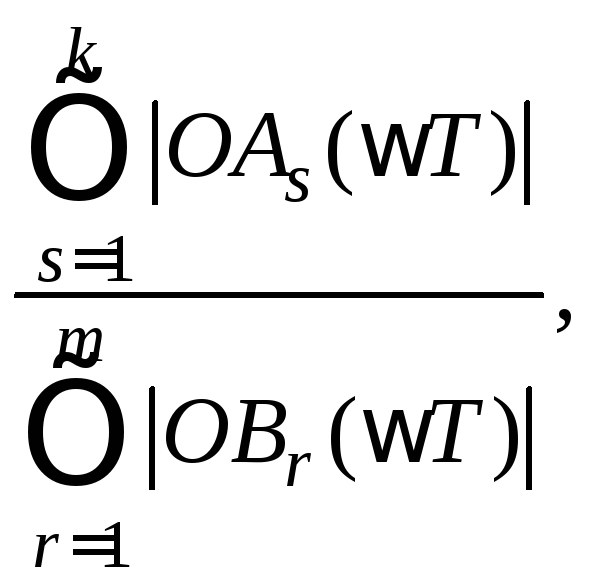
. (6.2.6)

Рассмотрим пример построения АЧХ с использованием (6.2.6) для ЦФ в виде апериодического звена (6.1.3) с параметрами с расположением действительного полюса на левой полуоси,(рис. 6.2.4а). Нетрудно видеть, чтоЛегко записать формулу для ПФ

На рис. 6.2.4б представлена рассматриваемая АЧХ. Отметим существенную особенность данной АЧХ из-за расположения полюса – при возрастании частоты АЧХ возрастает.

Рис. 6.2.4а. Геометрическая интерпретация ПФ

для апериодического звена на комплексной плоскости

Рис. 6.2.4б. АЧХ для цифрового апериодического звена

с действительным полюсом на левой полуоси

Учитывая возможность рассмотрения ПФ на комплексной плоскости с введённой переменной z, найдём связь между ПФ, как функции z, и импульсно-переходной функцией.

Запишем реакцию линейного фильтра с помощью импульсно-переходной функции, для простоты рассмотрения примем начальные условия нулевыми

.

На основании материалов разд. 2.6 можно сразу записать z-пре­образования для выходной последовательности на основе произведения z-преобразований входной и весовой последовательностей

Ясно, каким образом связывается импульсно-переходная функция и передаточная функция: ПФ на комплексной плоскости для принятой переменной z является z-преобразованием для импульсно-переходной функции.

6.2.2. Устойчивость ЦФ

Устойчивость ЦФ является исключительно важной характеристикой, которую необходимо принимать во внимание в задачах синтеза ПФ. Разберём определение устойчивости для ЦФ. Один из вариантов определения состоит в том, что ЦФ является устойчивым, если для любого ограниченного входного сигнала, поступающего на фильтр, выходной сигнал также является ограниченным. Это означает, что для входной последовательности с ограничением для которого выполняется неравенствопри любыхi, ЦФ является устойчивым, если для выходной последовательности существует значение ограничения которое обеспечивает для любыхi неравенство

Очевидно, что КИХ-фильтры всегда являются устойчивыми с точки зрения сделанного определения. Действительно, из разностного уравнения КИХ-фильтра при ограниченном входном сигнале и конечном числе ограниченных коэффициентов фильтра

при и

следует, что выходной сигнал также ограничен

При синтезе ПФ для БИХ-фильтров следует иметь в виду, что одна и та же структура БИХ-фильтра при одних значениях параметров может быть устойчивой, при других значениях – неустойчивой. Приведём здесь достаточные условия устойчивости БИХ-фильтров. Разберём простой пример, позволяющий прояснить существо подхода.

Пусть рассматривается БИХ-фильтр первого порядка с параметрами которые в общем случае являются комплексными. Запишем разностное уравнение и выражение для передаточной функции:

Полюс фильтра является единственным и может быть легко найден:Воспользуемся уже выведенной формулой (6.1.8) для связи выходного и входного сигнала

Из анализа этой формулы следует, что при и ограниченном входном сигналевсегда можно подобратьобеспечивающее неравенстводля любыхТаким образом, для того, чтобы БИХ- фильтр первого порядка оказался устойчивым, достаточно выполнение условия: модуль полюса ПФ должен быть меньше единицы– лежать внутри единичной окружности комплексной плоскости.

Разобранный пример позволяет сделать обобщение. Обратимся к выражению для ПФ произвольного БИХ-фильтра (6.2.5), рассмотрим формулу для сомножительне влияет на устойчивость. Положим, что у ПФ длянет кратных полюсов иТогда можно записать разложение исходной ПФ в виде суммы ПФ-составляющих

и выразить z-преобразование для выходного сигнала через сумму произведений z-преобразований входного сигнала и ПФ-со­ставляющих

Видно, что для обеспечения устойчивости рассматриваемого БИХ-фильтра достаточно выполнения условия: все модули полюсов для ПФ-составляющих должны быть меньше единицы должны лежать внутри единичной окружности комплексной плоскости.

Сформулированное достаточное условие не позволяет определить устойчивость в критическом случае для полюсов, лежащих на единичной окружности.

Проделаем анализ на устойчивость БИХ-фильтра второго порядка, рассмотрим пример цифрового резонатора (колебательного звена). Воспользуемся разностным уравнением из (6.1.4)

Передаточная функция представляется следующим образом:

=

Полюса этого БИХ-фильтра находятся из квадратного уравнения

Чтобы фильтр был резонатором, необходима комплексная сопряжённость полюсов, которая достигается при выполнении условия На рис. 6.2.2 на плоскости область таких параметров лежит выше параболыЧтобы полюса располагались внутри единичной окружности, необходимо выполнение неравенства

что соответствует области, лежащей ниже прямой Параметры на плоскостилежащие внутри луночки, обеспечивают устойчивость рассматриваемого цифрового резонатора.

Рис. 6.2.2. Область устойчивости цифрового резонатора