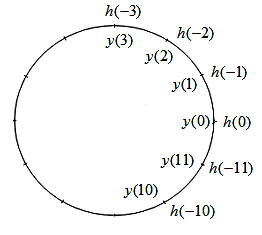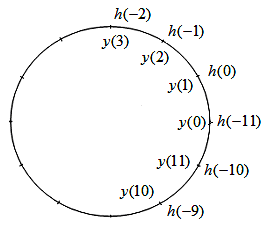Глава 5. Дискретные свёртки

5.1. Определения дискретных свёрток

Дискретные свёртки достаточно часто встречаются в различных задачах ЦОС, например при вычислении выходных сигналов линейных динамических систем. Приведём определения для дискретных свёрток, основываясь на предварительных сведениях, помещённых в разд. 1.2.2.

Пусть заданы две последовательности определённые в дискретных точках. Первая последовательностьслужит ядром свёртки, вторая последовательностьпредставляет собой дискретные значения входного сигнала. Будем полагать, что дискретные индексы для указанных последовательностей могут принимать значения в заданных диапазонах. Этим двум последовательностям ставится в соответствие выходная дискретная последовательностьУстанавливаются нижние и верхние пределы суммирования в свёрткахи пределы изменения индексовдля выходной последовательности. Дискретные свёртки с постоянными и с переменными пределами суммирования представляются формулами

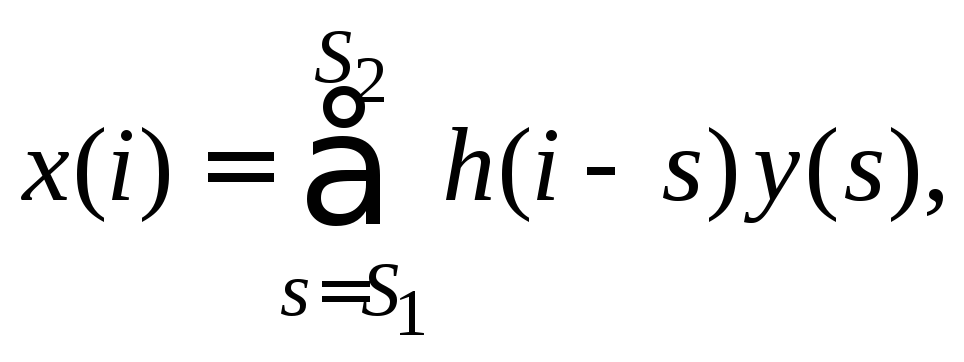
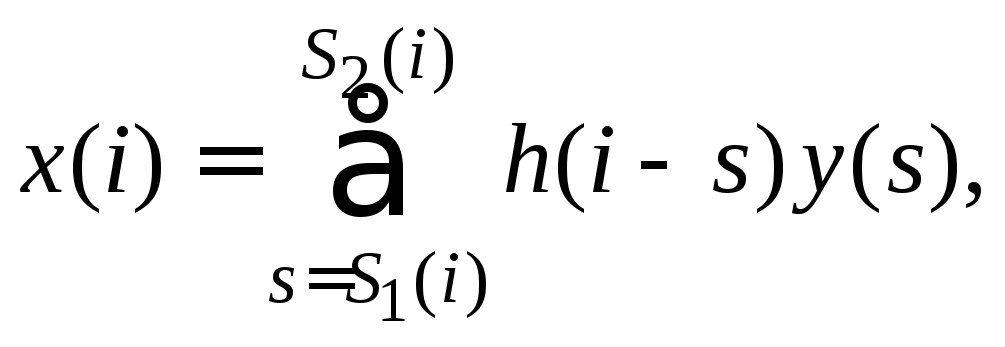
(5.1.1)

Свёртка двух бесконечных последовательностей определяется следующим образом:

(5.1.2)

Свёртки типа (5.1.2) называются линейными, их не следует путать с круговыми свёртками для периодических последовательностей, которые будут рассматриваться позже.

Целесообразно отметить существенное обстоятельство для свёрток – различное направление изменения (с разными знаками) индексов сомножителей при суммировании. Задачи, которые возникают при нахождении дискретных свёрток, состоят, в основном, в эффективном вычислении по точности и быстродействию выходной последовательности для заданных дискретных последовательностейс учётом их особенностей.

5.2. Вычисление прямых и обратных круговых свёрток

Перейдём к определению круговых свёрток (прямых круговых свёрток). Пусть заданы дискретные периодические с периодом N последовательности По определению дискретная круговая свёртка представляется выражением

(5.2.1)

Процедуру вычисления круговой свёртки удобно наглядно представить на круговых диаграммах, изображённых на рис. 5.2.1а, 5.2.1б в виде систем из внутренней и внешней окружностей, которые могут пошагово вращаться друг относительно друга.

Рис. 5.2.1а. Процедура вычисления круговой свёртки для i = 0, N = 12

Рис. 5.2.1б. Процедура вычисления круговой свёртки для i = 1, N = 12

Значения для периодического входного сигнала располагаются на внутренней окружности данной круговой диаграммы, значения для периодического ядра – на внешней окружности. Нахождение свёрткисводится к пошаговому вращению внешней окружности с последующим попарным умножением и суммированием. На рис. 5.2.1а, 5.2.1б проиллюстрировано вычисление

Сделаем в свёртке (5.2.1) замену переменных: Из равенстваполучаемизследуетТогда на основе изменения пределов суммирования записывается равенство для новой круговой свёртки:

Проанализировав вычисления на представленной круговой диаграмме, нетрудно заметить, что результат суммирования не изменится, если произвольно изменить точку начала и направление суммирования на круговой диаграмме. Справедливо равенство

(5.2.2)

Круговую свёртку в ряде случаев удобно представлять с по­мощью введения векторно-матричных переменных:

, ,

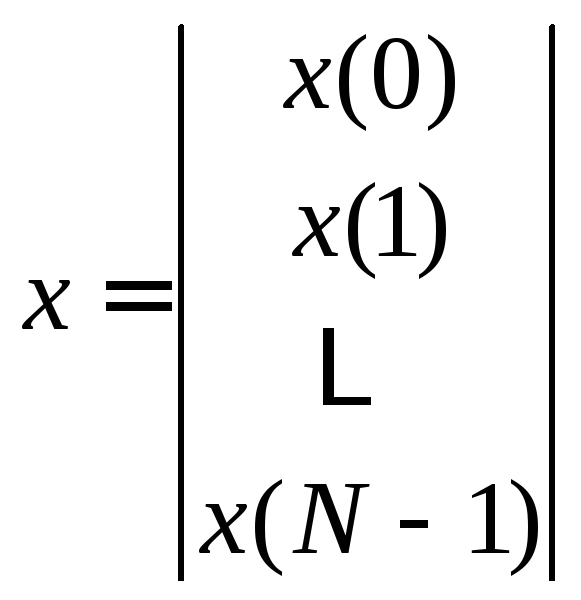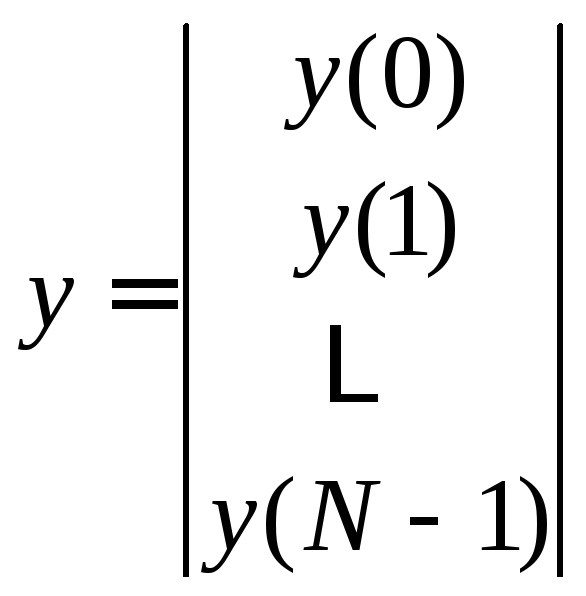, (5.2.3)

где выходные и входные векторы имеют размерностьматрица свёрткиH имеет размерность Результат свёртки с использованием (5.2.3) записывается в виде векторно-матричного произведения

Очевидно, что временные затраты на нахождение свёртки, если следовать в вычислениях непосредственно определению (5.2.2), (5.2.3), сравнимы с временными затратами на нахождение ДПФ по прямым формулам.

Рассмотрим алгоритм вычисления круговых свёрток, позволяющий существенным образом уменьшить временные затраты. Возьмём выражение для круговой свёртки (5.2.1), найдем ДПФ от его левой и правой части:

Переставив порядок суммирования, с учётом периодичности, получим

Окончательно запишем выражение в частотной области через произведения ДПФ

(5.2.4)

Круговые свёртки могут быть вычислены на основе обратного дискретного преобразования Фурье для произведений ДПФ входной последовательности и дискретной последовательности ядра:

Временные затраты по предлагаемому методу эквивалентны выполнению трёх ДПФ и N комплексных умножений. Выигрыш по времени при вычислении круговых свёрток в частотной области очевиден.

Рассмотрим алгоритм вычисления обратных круговых свёрток. Нахождение свёрток, о которых шла речь, обычно интерпретируется как прямая задача, связанная с определением выходной реакции линейной системы с известной импульсной переходной функцией на заданное входное воздействие. Однако возможна другая постановка, имеющая широкие приложения, состоящая в необходимости определения входного воздействия на линейную систему по известной выходной реакции и известной импульсно-переходной функции – эта задача интерпретируется как обратная.

Запишем выражение для дискретной круговой свёртки в скалярном и эквивалентном векторно-матричном виде

Нахождение вектора входного воздействия на систему по известному выходному векторуи квадратной матрице свёрткиH из (5.2.3) сводится к решению системы линейных уравнений и записывается в виде Решение подобной задачи во временной области сопряжено со значительными проблемами – необходимо, чтобы матрицаH имела ненулевой определитель – матрица должна быть хорошо обусловленной и размерность этой матрицы должна быть не очень большой, для обеспечения эффективного решения системы линейных уравнений. В большинстве практических задач последнее условие в ряде случаев трудно обеспечить.

Нахождение искомого вектора y, с учётом сказанного, удобно производить в частотной области с использованием процедур ДПФ. Воспользуемся сделанной записью свёртки (5.2.4) на основе ДПФ, выразим ДПФ для искомого входного вектора через отношение ДПФ выходного вектораx ДПФ переходной функции – ядра, и далее вычислим обратное ДПФ

Предложенное решение задачи – вычисление обратной свёртки в частотной области с точки зрения временных затрат, очевидно, значительно эффективнее процедуры решения во временной области.