Лабораторная работа № 1.4 «изучение законов колебаний при помощи математического и оборотного маятников»

I.Цель работы: определение ускорения свободного падения по периоду колебаний математического и оборотного физического маятников.

II.Описание установки.

О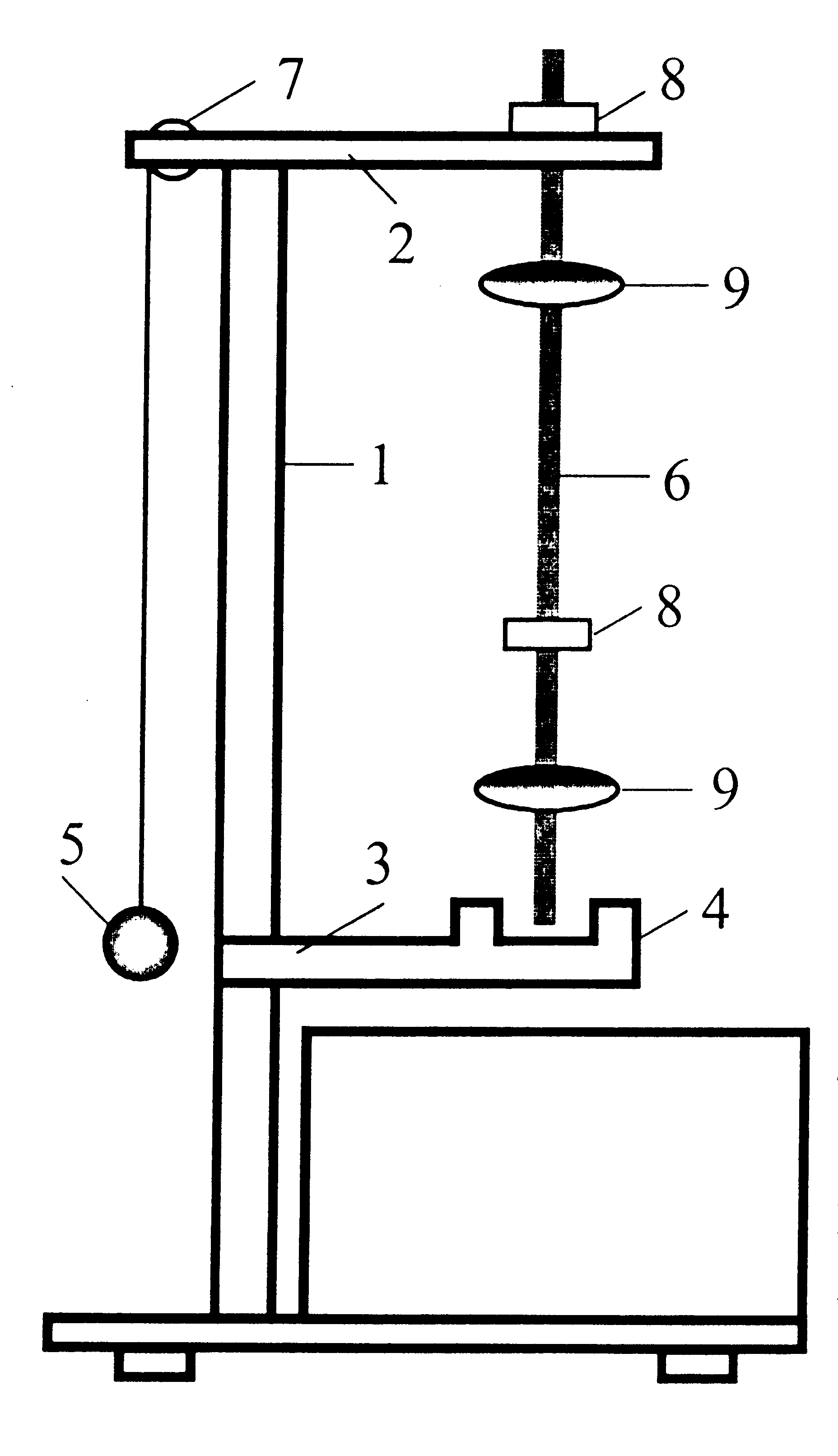бщий вид универсального маятника представлен на рисунке. К основанию прибора закреплена колонна 1, на которой зафиксирован верхний кронштейн 2 и нижний кронштейн 3 с фотоэлектрическим датчиком 4. С одной стороны кронштейна 2 находится математический маятник 5, с другой - оборотный маятник 6.

Длину математическою маятника можно регулировать с помощью воротка 7, и измерять с помощью шкалы на колонне 1. Оборотный маятник выполнен в виде стального стержня, на котором фиксированы два повернутые друг к другу лезвиями ножа 8 и два ролика 9.

На стержне через 10 мм нанесены кольцевые нарезки, служащие для точного определения длины оборотного маятника. Ножи и ролики можно перемещать вдоль оси стержня и фиксировать в любом положении.

Нижний кронштейн вместе с фотоэлектрическим датчиком тоже можно перемещать вдоль колонны и фиксировать в произвольно избранном положении.

III.Методика измерений и расчетные формулы.

Возможность определения ускорения свободного падения g по периоду колебаний математического маятника основана на том, что период гармонических колебаний математического маятника зависит только от его длины а и от ускорения свободного падения согласно формуле

(1)

Следует помнить о том, что данная формула справедлива только к том случае, когда на маятник действует единственная внешняя сила - сила тяжести. Так, если точка подвеса маятника участвует в некотором ускоренном движении, то наличествует еще одна внешняя сила - сила инерции.

Измерив длину математического маятника и период малых колебаний Т, можно рассчитать ускорение свободного падения по формуле:

В этих формулах а - расстояние от оси колебаний до центра масс колеблющегося тела (шарика).

В условиях данного опыта нельзя пренебречь размерами шарика d при определении длины маятника и считать ее равной длине нити l. Разница (a-l=d/2) дает относительную погрешность того же порядка, что и приборная погрешность определения Т и на порядок больше приборной погрешности измерения а.

В то же время на установке можно подобрать такую длину нити l, которая позволяет пользоваться приближенной формулой при расчете момента инерции, т.е. считать , как для материальной точки.

Чтобы исключить ошибки при определении а, связанные с неоднородностью шарика, искажением его формы и невозможностью достаточно точно определить положение оси колебаний, следует проделать два опыта с разной длиной а₁ и а₂, определить соответствующие периоды Т₁ и Т₂, и затем рассчитать g по разности (a₂ –a₁) и .

Из формулы (1) получаем:

, .

Таким образом, ускорение свободного падения равно:

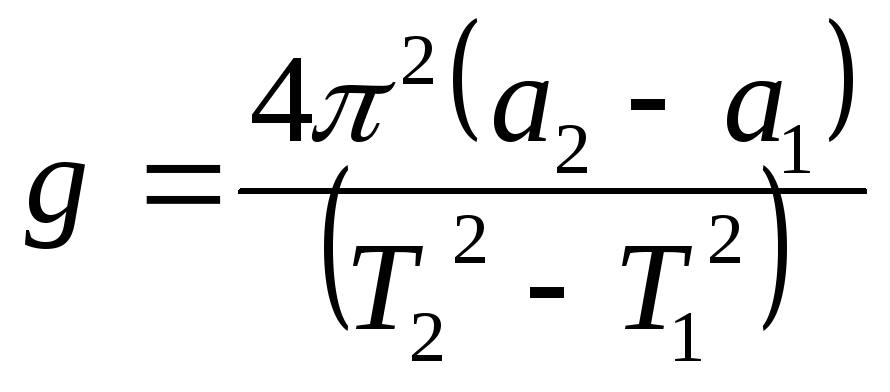. (2)

При малых колебаниях физический маятник совершает гармонические колебания с периодом

, (3)

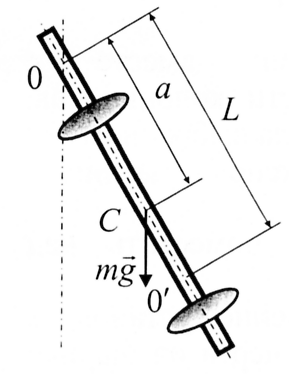гдеL - приведенная длина физического маятника: .

Введены обозначения: т - масса маятника, а- расстояние между точкой подвеса 0 и центром масс С маятника (см. рис.).

Точка 0', находящаяся на расстоянии приведенной длины L от точки подвеса называется центром качания физического маятника. Оказывается, что не всегда L > а. Точка подвеса 0 и центр качания 0' обладают свойством взаимозаменяемости: если ось подвеса сделать проходящей через центр качания, то прежняя точка подвеса станет центром качаний, а период колебаний физического маятника не изменится.

В процессе выполнения работы следует определить экспериментально положение центра качания, а также приведенную длину физического маятника.