
- •1.2 Действия над матрицами:
- •2. Определители
- •4 Системы линейных уравнений
- •4.2 Решение невырожденных линейных систем. Формулы Крамера:
- •4.3 Системы линейных однородных уравнений
- •Глава 2. Элементы векторной алгебры.
- •5. Векторы.
- •5.4 Проекция вектора на ось:
- •8.Смешанное произведение векторов
- •Глава 3: Комплексные числа
- •10. Действия над комплексными числами
- •10.1 Сложение: Суммой двух комплексных чисел
- •10.4 Деление
- •12.2 Предел функции при х→∞
- •12.3 Первый замечательный предел:
- •12.4 Второй замечательный предел:
5.4 Проекция вектора на ось:
Теорема 3: Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
Теорема 4: Проекции равных векторов на одну и ту же ось равны между собой.
6. Скалярное произведение векторов и его св-ва.
6.1 Определение скалярного произведения:
Скалярным
произведением двух не нулевых векторов
называется число равное произведению
длин этих векторов на косинус угла между
ними.Обозначивается:
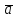 ·
·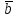 =
= ·
· ·
·
6.2 Св-ва скалярного произведения:
1) переместительное св-во:
 =
=
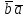
2) Сочетательное св-во:
( )
·
)
· =
=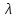 ·(
·(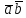 )
)
3) Распределительное св-во:
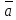 (
(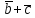 )
=
)
=
4) Скалярный квадрат вектора равен квадрату его длины:
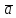 2
=
2
=
 2.
i2=-1
2.
i2=-1
5)
Если два вектора (ненулевые) взаимно
перпендикулярны, то их скалярное
произведение равно нулю.: т.е. если
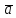

 ,то
,то = 0
= 0
6.3 Скалярное произведение в координатах.
Скалярное
произведение векторов равно сумме
произведений их одноимённых координат.
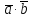 =ax
bx
+ ay
by
+ az
bz
=ax
bx
+ ay
by
+ az
bz
7. Векторное произведение векторов и его св-ва:
7.1 Определение векторного произведения:
Векторным произведением вектора а на вектор b называется вектор с который:
1) Перпендикулярен этим векторам
2) имеет длину численно равную площади параллелограмма построенного на этих векторах как на сторонах, т.е.
3) Данные векторы образуют тройку
Св-ва векторного произведения:
1)При перестановке сомножителей векторное произведение меняет знак, т.е
2) Сочитательное св-во:
3) Два не нулевых вектора коллинеарны тогда и только тогда,когда их векторное произведение = нулевому вектору
8.Смешанное произведение векторов
Определение смешанного произведения:
Смешанное произведение трёх векторов равно объёму параллелепипеда, построенного на этих векторах взятому со знаком «+», если эти векторы образуют правую тройку, и со знаком «-», если эти векторы образуют левую тройку.
Св-ва смешанного произведения
1) Смешанное произведение не меняется при циклической перестановке его сомножителей.
2) Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения.
3) Смешанное произведение меняет свой знак при перемене мест любых двух векторов – сомножителей.
4) Смешанное произведение ненулевых векторов а, b, c равно нулю тогда и только тогда, когда они компланарны.
Смешанное произведение в координатах
Пусть
заданы
векторы
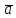 = ax
= ax + ay
+ ay + az
+ az ,
,
 = bx
= bx + by
+ by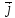 + bz
+ bz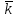 ,
,
 = cx
= cx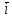 + cy
+ cy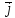 + cz
+ cz .
Найдём их
смешанное произведение.
.
Найдём их
смешанное произведение.
(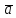 ×
×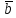 )
)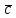 =
=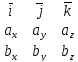 · (cx
· (cx + cy
+ cy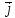 + cz
+ cz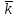 )
=
)
=
 –
–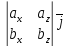 +
+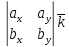 ·(cx
·(cx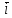 + cy
+ cy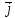 + cz
+ cz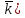 =
=
 -
- +
+

Короче
пишут так:
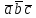 =
=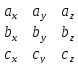
Глава 3: Комплексные числа
Понятие и представления комплексных чисел
Основные понятия
Комплексным числом z называется выражение вида
z = x + iy
Где (x , y) – действительные числа, а i - мнимая единица, i2 = -1
Формы записи комплексных чисел
1) Алгебраическая запись: z = x + iy
2) Тригонометрическая
запись: z
= r(cos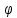 + i
sin
+ i
sin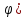
Модуль r
=
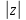 определяется по формулеr
=
определяется по формулеr
=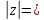
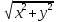
Формула Эйлера:
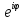 =
=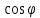 +
+
