Сибирская Государственная Геодезическая Академия

Реферат

По Высшей Математике

Выполнила: Карташова Екатерина Николаевна

Проверил: Могельницкий Б.С.

2012г

ОГЛАВЛЕНИЕ

Глава 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

§ 1. Матрицы......................................................

1.1. Основные понятия.......................................

1.2. Действия над матрицами................................

§ 2. Определители.................................................

2.1. Основные понятия................... . . . .... .............

2.2. Свойства определителей........................... ......

§ 3. Невырожденные матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1. Основные понятия... ....................................

3.2. Ранг матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 4. Системы линейных уравнений. . . . . . . . . . . . . . . . . . . . . . . . . . .

4.1. Основные понятия. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.3. Решение невырожденных линейных систем.

Формулы Крамера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.4. Решение систем линейных уравнений методом Гаусса. .

4.5. Системы линейных однородных уравнений. . . . . . . . . . . . . .

Глава 11. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

§ 5. Векторы.......................................................

5.1. Основные понятия.......................... . ................................. .

5.2. Линейные операции над векторами.......... ...........

5.3. Проекция вектора на ось. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§6. Скалярное произведение векторов и его свойства

6.1. Определение скалярного произведения ………………………….

6.2. Свойства скалярного произведения . . . . . . . . . . . . . . . . . . . . . .

6.3. Выражение скалярного произведения

через координаты. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 7. Векторное произведение векторов и его свойства. . . . . . . . . . . .

7.1. Определение векторного произведения ........... ........................

7.2. Свойства векторного произведения . . . . . . . . . . . . . . . . . . . . . .

§ 8. Смешанное произведение векторов.. . . . . . . . . . . . . . . . . . . . . . . . .

8.1. Определение смешанного произведения,

его геометрический смысл. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.2. Свойства смешанного произведения . . . . . . . . . . . . . . . . . . . . . ...

Глава 3. КОМПЛЕКСНЫЕ ЧИСЛА

§ 9. Понятие и представления комплексных чисел...............

9.1 Основные понятия.......................................

9.2. Геометрическое изображение комплексных чисел.. . . . ..

9.3.Формы записи комплексных чисел .....................

§ 10. Действия над комплексными числами. . . . . . . . . . . . . . . . . . . . . . .

10.1. Сложение комплексных чисел...........................

10.2. Вычитание комплексных чисел ................. . . . . . . ..

10.3. Умножение комплексных чисел.........................

10.4. Деление комплексных чисел ...... : . . . . . . . . . . . . . . . . . . . . .

10.5. Извлечение корней из комплексных чисел. . . . . . . . . . . . ..

Глава 4. ВВЕДЕНИЕ В АНАЛИЗ

§11. Функция. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.1. Понятие функции..... .. ....... .. ....... . . .. . . . . ... . .. .. .

§12. Предел функции

12.1. Первый замечательный предел. . . . . . . .. . . . . . . . . . . . . . . . . .

12.2. Второй замечательный предел................... .. ......

Глава1. Элементы линейной алгебры

1. Матрица

Основные понятия: Матрицей называется прямоугольная таблица чисел содержащая m строк одинаковой длины (или n столбцов одинаковой длины).Матрица записывается в виде:

A =

Или, сокращенно, А = (a_ij), где i = 1,m (т.е i = 1,2,3,…m) – номер

строки, j = 1, n (т.е. j = 1,2,3,…,n) – номер столбца.

Матрицу А называют матрицей размера m х n и пишут А_{m х n.} Числа a_ij, составляющие матрицу, называются её элементами.

Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Матрицы равны между собой,если равны все соответствующие элементы этих матриц, т.е.

А=В, если a_ij=b_ij, где i= 1,m, j=1,n.

Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера (n х n) называют матрицей n-го порядка.

Квадратная матрица, у которой все элементы,кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается Е.

Пример:

Е_зхз =

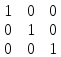
- единичная матрица 3-го порядка.

Матрица, все элементы которой равны нулю, называется нулевой.

Обозначается буквой О. Имеет вид:

О=

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно).

Вид:

А=

В=(b₁ b₂ b_3……b_n)

Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^Т.

Так, если А=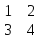, то А^Т =

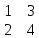
Транспонированная матрица обладает следующим св-ом: {А^Т}^T = A

Квадратная матрица называется невырожденной, если определитель не равен 0,если равен 0,то матрица – вырожденной.

Матрица А^-1 – обратной матрицей А, если выполняется условие:

Ах А^-1 = А^-1 х А =Е,

Где Е - единичная матрица того же порядка, что и матрица А.

Св-ва обратной матрицы: 1) det (A^-1) = 1/det A

2) (AxB)^-1 = B^-1 x A^-1

3)(A^-1) = (A^T)^-1

1.2 Действия над матрицами:

Сложение: Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц А_{m x n} = (a_ij) и B_{m x n} = (b_ij) называется матрица С_{m x n} = (c_ij) такая, что с_ij = a_ij + b_ij (i=1,m, j =1,n).

Пример:

+ =

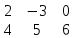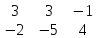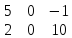
Аналогично определяется разность матриц.

Умножение на число:

Произведением матрицы А_{m x n} = (a_ij) на число k называется матрица В_{m x n} = (b_ij) такая, что b_ij = k x a_ij (i= 1,m, j= 1,n).

Пример:

А = 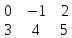,k = 2, A k =

Матрица -А= (-1) х А называется противоположной матрице А.

Операция сложения матриц и умножение матрицы на число обладают следующими свойствами:

1. A + B = B + A

2. A + (B + C) = (A + B) + C

3. A + O = A

4. A - A = O

5. 1 x A = A

6. c x (A+B) = cA + cB

7. (c + y)x A = cA + yA

8. c x (yA) = (cy) x A

где А,B,C – матрицы, с и y – числа.

Произведение матриц:

Операция умножение двух матриц возможно только, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А_{m x n} = (a_ij) на матрицу В_{n x p} =(b_jk) называется матрица С_{m x p} = (c_ik) такая, что

с_ik = a_i1 x b_2k + a_i2 x b_2k +…+a_inb_nk, где i= 1,m, k = 1,p,т.е.

элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца В.

Для операции транспонирования верны свойства:

1. (А + В)^Т =А^Т + В^Т

2. (АВ)^Т = В^Т х А^Т

2. Определители

1. Основные понятия:

Квадратной матрице А порядка n можно сопоставить число det A (или | A |, или ), называемое её определителем, следующим образом:

1. n = 1. A = 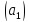; det A = a₁.

2. n = 2. A = 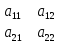; det A =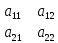= a₁₁a₂₂ – a₁₂ · a₂₁

3. n = 3. A = ; det A ==

= a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₂₁a₃₂a₁₃ – a₃₁a₂₂a₁₃ – a₂₁a₁₂a₃₃ – a₃₂a₂₃a_11.

Вычисление определителя 2-го порядка иллюстрируется схемой:

= -

Пример: 2 -3 = (2х6) – (5х(-3))= 12 – (-15)=27

5 6

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса),которое символически можно записать так:

= -

Пример: Вычислить определитель матрицы:

А =

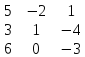
Решение:

Det A = 5 х1 х(-3) + (-2) х (-4) х 6 + 3 х0 х 1- 6х1х1 – 3 х (-2) х (-3) – 0 х (-4) х 5 = -15 + 48 - 6 – 18 = 9

1. Свойства определителей:

1 Свойство: («Равноправность строк и столбцов»). Определитель не изменяется, если его строки заменить столбцами, и наоборот.

2 Свойство: При перестановке двух параллельных рядов определитель меняет знак.

3 Свойство: Определитель, имеющий два одинаковых ряда, равен нулю.

4 Свойство: Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

5 Свойство: Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6 Свойство: («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

Минором некоторого элемента а_ij Определителя n-го порядка называется определитель n- 1-го, полученный из исходного путём вычёркивания строки и столбца, на пересечении которых находятся выбранный элемент. Обозначается m_ij:

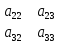Так, если =, тоm₁₁ = ,m₃₂ = .

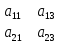Алгебраическим дополнением элемента а_ij определителя называется его минор, взятый со знаком «+», если сумма i+j – четное число, и со знаком ­«-», если эта сумма нечётная. Обозначается А_ij: А_ij = (-1)^i+j x m_ij.

Ранг матрицы: Наибольший из порядков миноров данной матрицы, отличных от нуля,- рангом матрицы. Обозначается r, r (A)

Или rang A.

Минор, порядок которого определяет ранг матрицы, - базисным. У матрицы может быть несколько базисных миноров.

Св-ва ранга матрицы:

1) При транспонировании матрицы её ранг не меняется.

2) Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3) ранг матрицы не изменится при элементарных преобразованиях матрицы.