4 Системы линейных уравнений

4.1 Основные понятия: Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, - система вида:

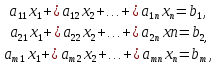
Где числа a_ij, i = 1,m, j=1,n называются коэффициентами системы, числа b_i - свободными членами. Подлежат нахождению числа X_n.

Такую систему удобно записывать в компактной матричной форме: А X = В

4.2 Решение невырожденных линейных систем. Формулы Крамера:

Пусть дана система в матричном виде: А · Х = B

Основная матрица А такой системы квадратная. Определитель этой матрицы:

=

называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.

Найдём решение системы уравнений в случаи

Умножив обе части уравнения на матрицу А^-1 , получим:

A^-1 · X = A^-1· B. Поскольку A^-1 · A = E и E · X = X, то

X = A^-1 · B.

Решение такой системы называется матричным способом.

Матричное равенство X = A^-1 · B запишем в виде:

= ·,

То есть =

=

Отсюда следует, что

X₁ =

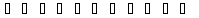
X_n =

Итак, х₁ = Аналогично х_2, х₃……х_n.

X_i = ,i =.

Называется формулами Крамера.

4.2 Метод Гаусса:

Одним из наиболее универсальных и эффективных методов решений линейных систем является метод Гаусса, состоящий в последовательном исключении неизвестных.

Процесс решения по методу Гаусса состоит из двух этапов:

1-этап. Прямой ход. Система приводится к ступенчатому виду.

На 2-ом этапе (обратный ход) имеет последовательное определение неизвестных из этой ступенчатой системы.

4.3 Системы линейных однородных уравнений

Теорема 1: Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r её основной матрицы был меньше числа n неизвестных т.е. r< n.

Теорема 2: Для того чтобы однородная система n линейных уравнений с n неизвестными имела нулевые решения, необходимо и достаточно, чтобы её определитель был равен 0.

Пример:

Решение: A = , r(A) = 2 (= 1) , n = 3

Так как r < n, то система имеет бесчисленное множество решений. Найдём их

= 2x₃, = 3x₃. Стало быть, х₁ =

= 2x₃, x₂ = =x₃ - общее решение.

Глава 2. Элементы векторной алгебры.

5. Векторы.

5.1 Основные понятия:

Вектор – это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А – начало вектора, то В – его конец. Длиной или модулем вектора АВ называется длина отрезка и обозначается |AB|. Нулевой вектор – вектор имеющий длину, которая равна 0. Не имеет направления.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через .

Векторы а и б называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записываются:

Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

5.2 Линейные операции над векторами.

Сложение: Пусть а и б – два произвольных вектора. Возьмём произвольную точку О и построим вектор ОА = а. От точки А отложим вектор АВ = б. Вектор ОВ, соединяющий начало первого вектора с концом второго, - суммой векторов а и б: =+.

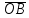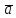Это правило сложения называют правилом треугольника

Сумму двух векторов можно построить также по правилу параллелограмма.

5.3 Произведением вектора на (число)называется вектор·который имеет длину·, коллинеарен вектору, имеет направление вектора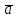, если> 0 и противоположное направление, если< 0.Например, если дан вектор, то векторы 3и -2буду иметь вид