
- •Методические указания и контрольные задания разработаны д.Т.Н., профессором Шутовым в.А., д.Т.Н., профессором Миренковым в.Е. И к.Т.Н., доцентом Полуэктовым в.А.
- •1. Цели освоение дисциплины
- •2. Содержание курса «теоретическая механика» и количество часов аудиторных занятий на рассмотрение его тем (л–лекции, п –практические занятия)
- •Распределение нагрузки в часах по неделям 2-го семестра
- •3.1 Рекомендуемая литература (основная)
- •3.2 Рекомендуемая литература (дополнительная)
- •4. Контроль знаний и успеваемости
- •4.2. Компьютерное тестирование (два задания на 30 минут каждое).
- •4.3. Форма учета текущего контроля успеваемости
- •5. Задания к контрольным работам и требования к их оформлению
- •Контрольная №1. Определение реакций опор балок
- •Контрольная №2. Определение реакции опор рам
- •Контрольная №3. Определение усилий в стержнях фермы
- •Контрольная №4. Определение положения центра тяжести плоской фигуры
- •6. Общие положения основ теории статики
- •6.1. Связи и их реакции, нагрузки
- •6.2. Система сходящихся сил
- •6.3.Плоская система сил
- •6.3.1. Условия равновесия плоской системы сил
- •6.4.Расчет ферм
- •Определение опорных реакций
- •Определение усилий в стержнях фермы
- •6.5.Центр тяжести
6.2. Система сходящихся сил
Систему сил называют сходящейся, если линии их действия пересекаются в одной точке.
Теорема: система сходящихся сил![]() эквивалентна ()
эквивалентна ()![]() одной силе
одной силе![]() ,
называемой равнодействующей, которая
равна геометрической сумме всех сил
системы и проходит через точку пересечения
линий их действия
,
называемой равнодействующей, которая
равна геометрической сумме всех сил
системы и проходит через точку пересечения
линий их действия
![]() ,
,![]()
Силовым многоугольникомсистемы
сходящихся сил называют многоугольник,
построенный на ее векторах (силах).
Построение многоугольника можно
осуществить в произвольном порядке
так, чтобы конец одного вектора являлся
началом другого, переносимого параллельно
его линии действия. Вектор![]() ,
замыкающий силовой многоугольник,
начало и конец которого совпадают
соответственно с началом первого и
концом последнего векторов системы,является геометрической суммой этой
системы сил.
,
замыкающий силовой многоугольник,
начало и конец которого совпадают
соответственно с началом первого и
концом последнего векторов системы,является геометрической суммой этой
системы сил.
Зачастую величину и направление равнодействующей удобнее определять аналитически. Так, если за систему отсчета принять прямолинейные ортогональные оси координат Oxyz, то, в частности, задачу о сложении сил можно решить с помощью следующих соотношений
![]()
![]() ,
,
![]() ,
,
где
![]() -
проекции
-
проекции![]() соответственно на осиx,y,z;l,m,n-
направляющие косинусы
соответственно на осиx,y,z;l,m,n-
направляющие косинусы![]() .
.
Существуют геометрическая и аналитическая формы условий равновесия системы сходящихся сил:
- (геометрическая) для равновесия системы сходящихся сил необходимо и достаточно, чтобы ее силовой многоугольник был замкнут;
- (аналитическая) для равновесия системы сходящихся сил необходимо и достаточно равенства нулю сумм проекций всех сил системы на оси координат
![]()
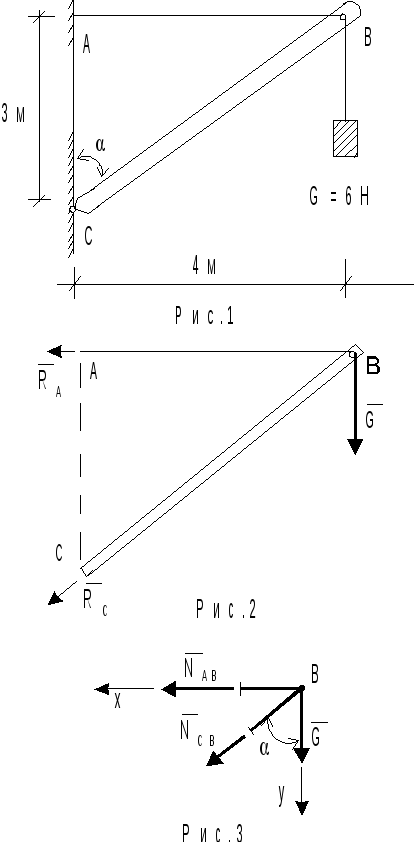
Строим силовую схему рассматриваемой
конструкции (рис.2). Реакция закрепления
нити в точке А направлена по ее оси.
Линии действия
![]() и
и![]() пересекаются в точке В, а поскольку
система находится в равновесии, то на
основании теоремы о трех силах можно
заключить, что линия действия реакции
пересекаются в точке В, а поскольку
система находится в равновесии, то на
основании теоремы о трех силах можно
заключить, что линия действия реакции![]() в шарнирно-неподвижной опоре С направлена
по оси СВ.
в шарнирно-неподвижной опоре С направлена
по оси СВ.
Любая часть конструкции, находящейся
в равновесии, также находится в равновесии,
что позволяет рассмотреть равновесие
узла В (рис.3). Действие отброшенной части
на рассматриваемую, согласно аксиоме
о действии и противодействии, заменим
усилиями
![]() ,
которые и являются искомыми по условию
задачи. ОпределениеNAB,NCBуже можно проводить как аналитически
с помощью условий равновесия
,
которые и являются искомыми по условию
задачи. ОпределениеNAB,NCBуже можно проводить как аналитически
с помощью условий равновесия
![]()
![]()
т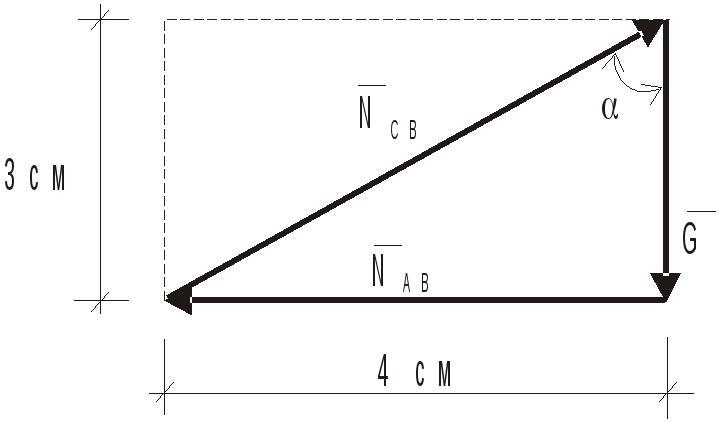 ак
и графически, путем построения силового
многоугольника, который в масштабе в 1
см 2 Н изображен на рисунке. Знак минус
при найденном значенииNCB
указывает на то, что истинное
направление
ак
и графически, путем построения силового
многоугольника, который в масштабе в 1
см 2 Н изображен на рисунке. Знак минус
при найденном значенииNCB
указывает на то, что истинное
направление![]() противоположно показанному на рис.3,
т.е. стержень СВ сжат.
противоположно показанному на рис.3,
т.е. стержень СВ сжат.
