1.5. Вычисление поправок в направления за центрировку теодолита и редукцию визирной цели
На пунктах триангуляции, на которых выполнены угловые измерения , проекции точки J стояния теодолита, визирной цели знака S и центра знака С на горизонтальную плоскость не совпадают между собой (рис.1.2).
Рис.1.2. К вычислению поправок за центрировку и редукцию.
В связи с этим все измеренные на пункте направления должны быть приведены к его центру в точке С, т.е. исправлены поправками с за центрировку теодолита.
Эти поправки прибавляются со своим знаком к значениям измеренных на данном пункте направлений.
Поправки r за редукцию визирной цели S данного пункта вводятся со своим знаком в обратные направления, поскольку визирование со смежных точек производится не на центр данного пункта в точке С , а на его визирную цель в точке S.
Поправки за центрировку теодолита (c") и редукцию визирной цели (r") вычисляют по формулам:
,
,
(5)
где
,
,
,
-
соответственно графические элементы
центрировки и редукции (табл.3); М
– значения измеренных направлений
(табл.3), для которых вычисляются
поправки; S–
расстояние между пунктами (из таблицы 4);
.
Значения
угловых элементов центрировки и редукции
,
должны
быть определены относительно направления,
выбранного на данном пункте за исходное.
На практике значения этих углов могут
быть определены относительно произвольного
направления. Например, для пункта 1
угловой элемент редукции для использования
в формулах (5) должен быть определен на
пункт 2, в примере, по результатам
измерений его значение определено на
пункт 6. В этом случае полученное значение
необходимо привести к исходному
(нулевому) направлению по формуле:
,
(6)
где
-
угловой элемент редукции, приведенный
к «нулевому» направлению;
-
угловой элемент редукции, определенный
на направление М
.
Пример.
Исходное
направление – пункт 2, значение
направления, округленное до целых минут-
М1-6
равно
100°33΄,
значение углового элемента редукции
на пункт 6 равно
=
120°18΄, значение углового элемента
редукции на исходный пункт 2 вычисляется
по формуле (6).
Поправки за центрировку и редукцию вычисляют до 0.1, по формулам (5).
Вычисление поправок производится в таблице 5.
Пример.
Для
направления
графические элементы центрировки
отсутствуют (теодолит при измерениях
центрировался непосредственно над
центром пункта), поправка за центрировку
не вычисляется. По значениям графических
элементов редукции
,
взятых из табл.3 и приведенных к «нулевому»
направлению по формуле (6) вычисляется
поправка за редукцию визирной цели,
при этом из таблицы 4 выписывают значение
длины стороны треугольника (
-
сторонаI
треугольника против вершины 7).
Вычисленное значение вписывают в графу 8 таблицы 5.
Таблица 5
Вычисление поправок за центрировку и редукцию
-
Назв. пункта
Назвнапр
M
M+
M+
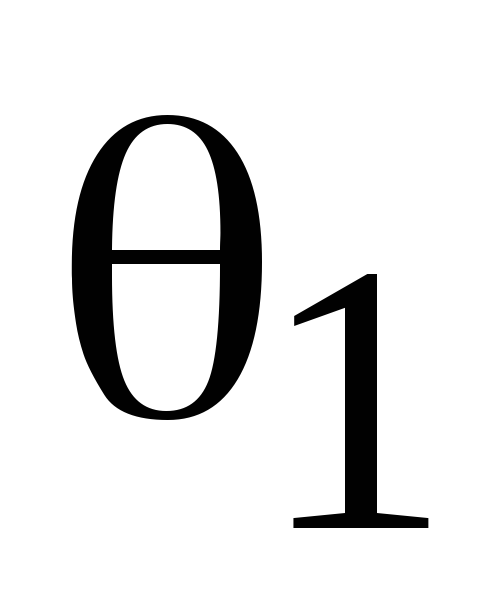
S, м
c"
r"
1
2
3
4
5
6
7
8
2
0
0
0,0
19
45
0,0
1196
+13,1
1
7
28
20
50,9
48
05
50,9
964
+35,8
6
100
33
23,5
120
18
23,5
2024
+19,8
3
0
0
0,0
160
00
0,0
2470
+0,3
2
7
103
19
35,4
263
19
35,4
575
-4,3
1
156
2
39,2
316
02
39,2
1196
-1,4
4
0
0
0,0
3
7
82
40
27,4
2
94
48
18,3
5
0
0
0,0
241
00
0,0
2245
-0,2
4
7
99
37
23,1
340
37
23,1
3524
-0,1
3
148
9
16,6
29
09
16,6
2673
+0,1
4
0
0
0,0
270
0
0,0
2245
-1,4
5
6
286
49
4,0
196
49
4,0
3187
-0,3
7
309
12
15,9
219
12
15,9
4484
-0,4
1
0
0
0,0
50
30
0,0
104
30
0,0
2024
+1,2
+55,5
6
7
27
56
44,1
78
26
44,1
132
26
44,1
1958
+1,5
+43,8
5
147
14
0,9
197
44
0,9
251
44
0,9
3187
-0,3
-34,6
1
0
0
0,0
17
0
0,0
964
+4,8
2
98
56
53,8
115
56
53,8
575
+24,5
7
3
163
28
59,5
180
28
59,5
2663
+0,0
4
212
16
36,1
229
16
36,1
3524
-3,4
5
241
51
23,6
258
51
23,6
4484
-3,4
6
280
9
36,1
297
9
36,1
1958
-7,1