
- •1. Предварительные вычисления и уравнивание сети триангуляции
- •Журнал измерения горизонтальных направлений круговыми приемами
- •1.2. Составление сводки результатов измерений горизонтальных направлений и вычисление величины средней квадратической ошибки измеренного направления
- •Сводка измеренных направлений
- •1.3. Составление рабочей схемы сети
- •Исходные данные, средние значения измеренных направлений и элементы приведения
- •1.4. Предварительное решение треугольников
- •Предварительное решение треугольников
- •1.5. Вычисление поправок в направления за центрировку теодолита и редукцию визирной цели
- •Вычисление поправок за центрировку и редукцию
- •1.6. Вычисление поправки за кривизну изображения геодезической линии на плоскости в проекции Гаусса- Крюгера
- •1.7. Составление таблицы направлений, приведенных к центрам пунктов и редуцированных на плоскость в проекции Гаусса-Крюгера
- •1.8. Оценка точности результатов измерений по значениям невязок фигур и свободных членов синусных условий
- •Вычисление невязок треугольников
- •Вычисление коэффициентов и свободного члена базисного условного уравнения
- •1.9. Уравнивание триангуляции коррелатным способом
- •1.9.1. Краткие сведения из алгоритма способа
- •1.9.2. Расчет числа независимых условных уравнений
- •1.9.3. Угловые условия (фигур, горизонта, азимутов)
- •Условие горизонта на пункте 7
- •1.9.4. Полюсное условие
- •1.9.5. Базисное условие
- •1.9.6. Составление матрицы коэффициентов условных уравнений. Окончательные вычисления
- •Вычисление уравненных значений углов и решение треугольников
- •Вычисление координат точек сети триангуляци
- •Каталог координат пунктов сети триангуляции
- •2. Предварительная обработка хода полигонометрии
- •2.1. Предварительная обработка полигонометрии (исходные данные)
- •Исходные данные
- •Измеренные длины и превышения
- •Значения измеренных направлений и элементов приведения
- •2.1.1. Приведение линейных измерений к центрам пунктов и редуцирование горизонтальных проложений на плоскость в проекции Гаусса-Крюгера
- •Вычисление высотных отметок точек хода
- •Вычисление приближенных координат пунктов полигонометрии
- •2.1.2. Приведение измеренных направлений к центрам пунктов и редуцирование на плоскость в проекции Гаусса-Крюгера
- •Приведение измеренных направлений к центрам пунктов и редуцирование на плоскость в проекции Гаусса-Крюгера
- •Приведение измеренных расстояний к центрам пунктов и редуцирование на плоскость проекции Гаусса-Крюгера
- •3. Уравнивание геодезической сети параметрическим способом
- •3.1. Краткие сведения из алгоритма способа
- •3.2. Уравнивание сети трилатерации параметрическим методом
- •Значения измеренных сторон, приведенных к центрам знаков и редуцированных на плоскость
- •Вычисление приближенных координат пунктов полигонометрии
- •Матрица коэффициентов уравнений поправок и вектор свободных членов
- •Вычисление длин по уравненным координатам
- •4. Уравнивание нивелирной сети способом узлов (приближений)
- •Вес уравненной отметки репера определяется из соотношения:
- •Вычисление высот узловых точек
- •Каталог уравненных высот
- •Литература
Матрица коэффициентов уравнений поправок и вектор свободных членов
|
|
x3 (м) |
y3 (м) |
x4 (м) |
y4 (м) |
X5 (м) |
Y5 (м) |
|
|
1 - 3 |
-0,7383 |
+0,6744 |
0 |
0 |
0 |
0 |
0 |
|
1 - 4 |
0 |
0 |
-0,8815 |
-0,4722 |
0 |
0 |
0 |
|
2 - 3 |
-0,9997 |
-0,0251 |
0 |
0 |
0 |
0 |
-0,3563 |
|
2 - 4 |
0 |
0 |
-0,6041 |
-0,7969 |
0 |
0 |
0 |
|
2 - 5 |
0 |
0 |
0 |
0 |
-0,2042 |
+0,9789 |
-0,0986 |
|
3 - 4 |
+0,0562 |
+0,9984 |
-0,0562 |
-0,9984 |
0 |
0 |
0 |
|
3 - 5 |
-0,6962 |
-0,7178 |
0 |
0 |
+0,6962 |
+0,7178 |
0 |
Решение системы уравнений поправок выполняется с помощью специальных программ. Технология образования векторов и матриц в Mathсad описана в коррелатном способе уравнивания п.1.9.6.
Запишем матрицу коэффициентов уравнений поправок, вектор свободных членов и матрицу весов с помощью средств Mathcad:
А:=
L:=
P:=
Переходим к системе нормальных уравнений:
![]()
и вычисляем значения обратной матрицы нормальных уравнений

Используя свойство обратной матрицы, проконтролируем правильность вычислений. Для этого необходимо перемножить матрицу нормальных уравнений и обратную к ней:

Для решения нормальных уравнений вектор b и окончательное решение системы нормальных уравнений:
![]()
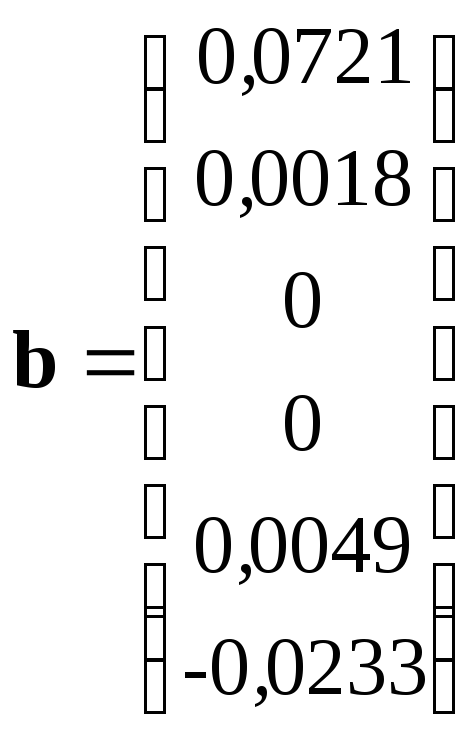
![]()

Принимая во внимание решение системы нормальных уравнений, находим решение системы уравнений поправок по формуле (22), в результате получим вектор поправок в измеренные величины (значения поправок в метрах):
![]()
V=
6. Производим оценку точности по результатам уравнивания. Для этого вычисляем величину ошибки единицы веса по формуле 25 и средние квадратические ошибки определения параметров:
![]()

7. На заключительном этапе уравнивания вычисляют уравненные длины (табл.28), составляют каталог уравненных координат (табл. 29) и выполняют контрольные вычисления.
Контрольные вычисления подразумевают вычисление длин по уравненным координатам и сравнение их с уравненными длинами.
Таблица 28
-
Вычисление уравненных длин линий
Длины, м
V, м
Уравненные
длины, м
1 – 3
3026,181
+0,0457
3026,227
1 – 4
2747,965
-0,0379
2747,927
2 – 3
2389,343
-0,0271
2389,316
2 – 4
4264,458
+0,1009
4264,559
2 – 5
2019,859
0
2019,859
3 – 4
3343,757
-0,0359
3343,721
3 – 5
2836,926
0
2837,926
Таблица 29
-
Вычисление уравненных координат
Приближённые координаты, м
Поправки, м
Уравненные координаты, м

м
X3
6011221,966
-0,3137
6011221,652
0,0912
Y3
2375243,443
-0,2757
2375243,167
0,1656
X4
6011033,982
+0,1865
6011034,169
0,1730
Y4
2371904,974
-0,2680
2371904,706
0,1920
X5
6013197,845
-0,5754
6013197,270
0,2382
Y5
2377280,530
-0,0219
2377280,508
0,0883
Таблица 30
