3.2. Уравнивание сети трилатерации параметрическим методом

Студенту предлагается уравнять четырехугольник трилатерации параметрическим способом. Данные представлены в приложении 3. Последовательность уравнительных вычислений проследим на примере сети, изображенной на рис. 3.1.

Р

ис.3.1. Схема сети трилатерации

Таблица 24

Исходные данные
Пункт	X (м)	Y (м)
1	6013456,321	2373202,505
2	6013610,202	2375303,311

Таблица 25

Значения измеренных сторон, приведенных к центрам знаков и редуцированных на плоскость

Сторона	Длины сторон, (м)
1 – 3	3026,181
1 – 4	2747,965
2 – 3	2389,343
2 – 4	4264,458
2 – 5	2019,859
3 – 4	3343,757
3 – 5	2836,926

Стороны в данной сети приведены к центрам знаков и редуцированы на плоскость в проекции Гаусса-Крюгера, последовательность предварительной обработки измерений описана в предыдущих параграфах. Координаты исходных пунктов представлены в таблице 24, измеренные величины в таблице 25.

В сети измеренными величинами являются длины (n=7), в качестве независимых параметров выберем координаты пунктов 3,4 и 5 (k=6). Далее вычислительный процесс можно разбить на этапы.

1. Согласно алгоритму способа составляем 7 уравнений связи измеренные длины функционально связаны с параметрами (координатами) формулами обратной геодезической задачи:

,

,

,

,

,

,

.

2. Определяем веса измеренных величин по формуле , где С=100, принимается условно, чтобы значения весов были близкими к единице, поскольку длины в сети трилатерации измерены светодальномером СТ-5, для вычисления средней квадратической ошибки измерения используем уравнение светодальномера:

, коэффициенты a = 10 мм и b = 5 мм соответствуют светодальномеру СТ-5, D – расстояние в километрах.

Пример.

Средняя квадратическая ошибка измеренной стороны 1-3:

, ,

Вес стороны 1-3:

Составляем матрицу весов. Вычисленные веса округляют и записывают по главной диагонали в соответствии с номером уравнения связи. В результате образуется матрица весов измеренных длин размерностью 7х7.

Пример.

3. Вычисляем предварительные значения параметров (в нашем случае координат пунктов 3 и 4,5). Для вычисления предварительных значений координат можно воспользоваться различными способами. Например, метод линейной засечки. Для примера вычислим координаты пункта 3:

,

,

Где ,

,

Пример.

6013456.321 – 6013610.202 = -153.881 м,

2373202.51 – 2375303.31 = -2100.806 м,

= 2106.434 м,

,

= .

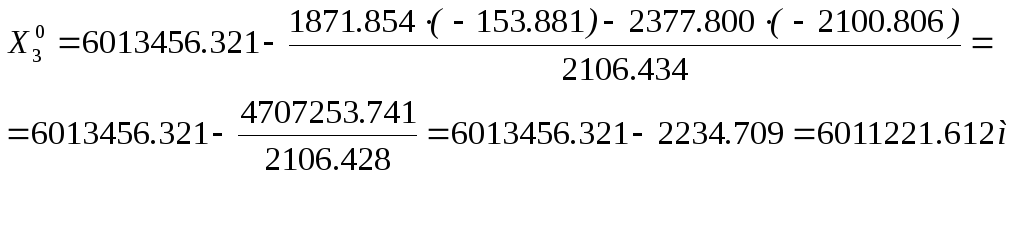
Другой способ вычисления координат подразумевает вычисления в теодолитном ходе, условно проложенном по пунктам сети трилатерации. Для реализации этого метода необходимо вычислить углы в треугольниках, используя теорему косинусов. Для треугольника, образованного пунктами 1, 2, 4:

,

Из предыдущего уравнения следует:

.

Пример.

При вычислении углов стоит обратить внимание, что для теодолитного хода при пунктах 2 и 3, представляют собой сумму углов, вычисленных в треугольниках 1,2,3 и 2,5,3 для вершины 2 и треугольниках 4,2,3 и 3,5,2 для вершины 3.

Дальнейшие вычисления производят в таблице 26.

Для дальнейших вычислений используем значения приближенных координат, вычисленных вторым способом.

Таблица 26