2.4 Определение доверительных границ случайной погрешности результата измерения

Доверительные границы результатов измерений определяются как наибольшее и наименьшее значение результатов измерений ограниченные интервалом, внутри которого с заданной вероятностью находится искомое истинное значение измерения.

Полученный доверительный интервал удовлетворяет условию (формула 2.21):

(2.21)

где n – число измерений значений; t_гр расчитывается по формуле 2.22:

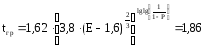(2.22)

Половина длины доверительной интервала называется доверительной границей погрешности результата измерений и вычисляется по формуле 2.23.

ε=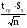(2.23)

Следовательно результат измерения можно записать так:

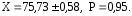_(2.24)

2.5 Определение доверительных границ не исключенной систематической погрешности

Не исключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть не исключенные систематические погрешности метода, средства измерения, а также вызванные другими источниками.

В качестве границ составляющих не исключенной систематической погрешности принимают, например пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежительно малы.

Границы не исключенной систематической погрешности  результата измерения вычисляют путем построения композиции не исключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерной распределении не исключенных систематических погрешностей эти границы можно вычислить по формуле 2.25:

(2.25)

где _i – граница i-ой не исключенной систематической погрешности;

k- коэффициент, определяемый принятой доверительной вероятностью;

m – число суммируемых погрешностей.

Коэффициент k принимают равный 1,1 при уровне доверительной вероятности Р=0,95.

В гигрометре психрометрическом типа ВИТ-1погрешность равная 0,02. Подставив это значение в формулу 2.26 получим следующие выражение:

(2.26)

2.6 Определение границ погрешности измерения

Для определения границ погрешности результата измерения необходимо определить отношение 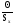. По его величине можно судить о возможности пренебрежения (или наоборот) систематической погрешностью. Если оно больше 8, то граница погрешности результата равна Δ=. А если отношение меньше 0,8, то граница погрешности результата равна Δ=. В случае, когда оно лежит в границах от 0,8 до 8 то прибегают к соответствующему расчету.

Рассчитав данное соотношение получаем

, а значит неисключенной систематической погрешностью пренебрегают по сравнению со случайной пренебрегают и принимают, что граница погрешности результата Δ=0,58.

Окончательный результат измерения влажности производственного помещения с помощью гигрометра психрометрического типа ВИТ-1 можно представить в следующем виде:

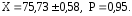_(2.24)

28