ОиАС-4

Требуется найти u(t), при котором объект (2.2.26) переходит из состояния (2.2.29) в состояние (2.2.30), при этом выполняются ограничения (2.2.27), а функционал (2.2.28) принимает наименьшее значение.

2

Переходя к определению оптимального управления на основе принципа максимума, сформируем гамильтониан

Уравнения (2.2.26), (2.2.32), (2.2.33) составляют краевую задачу. Переходя к ее исследованию, запишем решение системы (2.2.32):

где а>0; 0 α 2π – неизвестные числа, которые необходимо определить так,

чтобы управление (2.2.33) привело объект (2.2.26) в состояние (2.2.30). Найдем

3

решение системы (2.2.26) при u = 0, u = 1, u = –1.

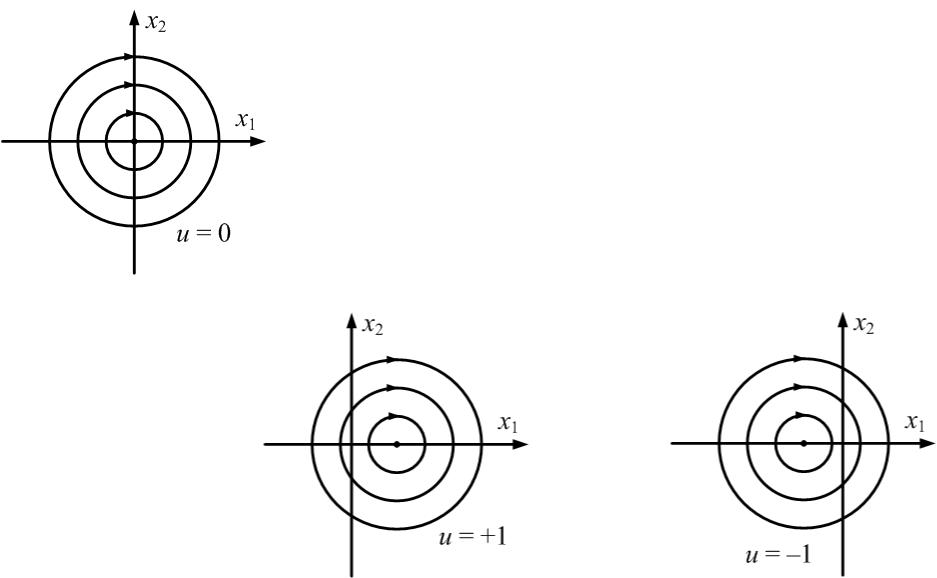
В первом случае решение этой системы имеет вид x1=–R cos(t + β), x2=R sin(t + β). Оно зависит от постоянных R и β при этом R > 0, 0 β 2π. Фазовые траектории этой системы представляют собой окружности с центром в начале координат.

Фазовые траектории системы (2.2.26) при u= + 1 и u = –1 также являются окружностями, центры которых расположены в точках (1,0) (–1, 0)

соответственно.

4

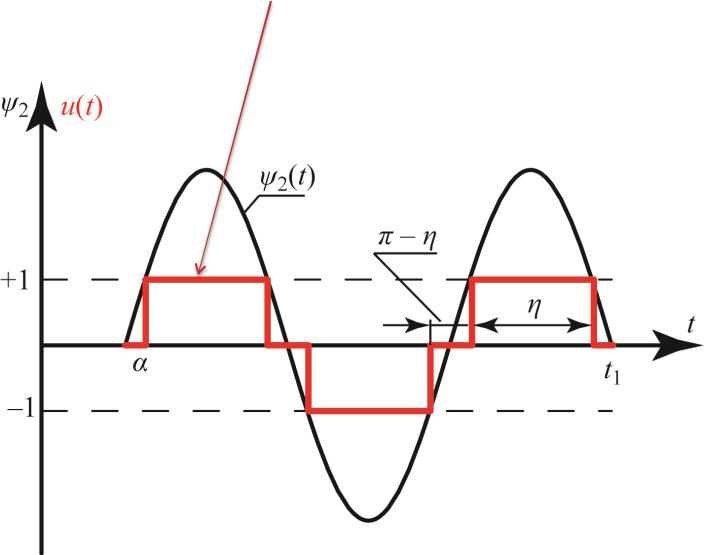
Пусть некоторым оптимальным управлениям u(t) объект (2.2.26) переводится из начального состояния (x10, х20) в начало координат. Тогда на последнем участке оптимальной траектории управление u(t) равно +1 либо –1. Для определенности будем полагать, что оптимальное управление имеет вид, изображенный на рисунке.

5

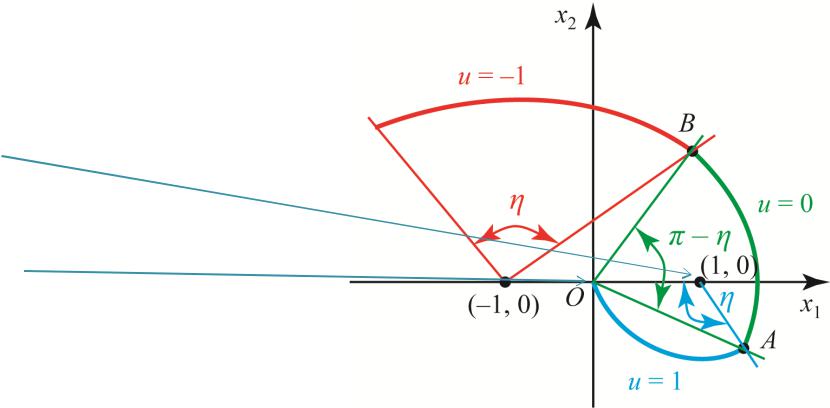
В этом случае последний участок фазовой траектории представляет собой дугу величиной η с центром в точке (1, 0) . Управление u(t)=0 при

t [t1 – π; t1 – η], и поэтому соответствующий участок фазовой

траектории является дугой с центром в точке (0, 0) и центральным углом

π – η.

В точке А происходит переключение управления u(t)=0 на u(t) = l, а в точке В – с u(t)=–1 на u(t)=0. Задаваясь различными значениями чисел α и а, получим различные числа η. Строя для каждого числа η траекторию методом «попятного движения, определяем, «попал» ли левый конец этой траектории в точку (x10, х20). Пусть для некоторого η траектория ОАВ прошла через точку (x10, х20). Для такого числа η нетрудно определить числа α и а, а через них начальные условия ψ10, ψ20, которые и разрешают краевую задачу.

6

Если один из концов траектории x(t), например правый, закреплен, то граничные условия имеют вид

8

Пример 2.2.2. Определить оптимальное управление в следующей задаче оптимального управления:

максимум достигается, когда управление принимает граничные значения и его

знак совпадает со знаком функции ψ2, т.е. при u = аsignψ2.

9

Так как знак линейной функции может измениться только один раз, то оптимальным может быть управление

В частности, если ts = 10, то это значит, что функция ψ2 на интервале [0,10] не меняет знака, и управление не переключается. Выбор из двух управлений можно сделать исходя из того, какое из этих управлений обеспечивает выполнение граничных условий. Но в данном примере этот выбор можно сделать на оснований физических соображений. По условию задачи нужно повернуть вал двигателя на максимальный угол и остановить его за заданное время. Поэтому оптимальным может быть только первое из двух приведенных управлений. Остается определить только момент ts переключения управления.

10