
матан отвты / теория / 29
.docМножество R элементов x, y, z, ... любой природы называется линейным (или векторным) пространством, если выполнены следующие три требования:
Существует правило, посредством которого любым двум элементам x и y множества R ставится в соответствие третий элемент z этого множества, называемый суммой элементов x и y и обозначаемый z=x+y.
Существует правило, посредством которого любому элементу x множества R и любому вещественному числу α ставится в соответствие элемент w этого множества, называемый произведением элемента x на число α и обозначаемый w=αx или w=xα.
Представленные два правила подчинены следующим восьми аксиомам:
x+y=y+x (переместительное свойство суммы);
(x+y)+z=x+(y+z) (сочетательное свойство суммы);
существует нулевой элемент 0 такой, что x+0=x для любого элемента x.
для любого элемента x существует противоположный элемент элемент x' такой, что x+x'=0;
1·x=x для любого x;
λ(μx)=(λμ)x (сочетательное свойство относительно числового множителя);
(λ+μ)x=λx+μx (распределительное свойство относительно числовых множителей);
λ(x+y)=λx+λy (распределительное свойство относительно суммы элементов).
Элементы линейного (векторного) пространства называются векторами.
Векторное пространство называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.
Размерность пространства условимся обозначать через dim.
Например, размерность множества всех плоских векторов равна 2, размерность множества пространственных векторов равна 3.
Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.
Совокупность n линейно независимых векторов n- мерного векторного пространства называется его базисом.




Теорема 1. Если функция f(x) n раз дифференцируема в точке x0, то в некоторой окрестности этой точки
|
|
(14.10) |
Многочлен
|
|
(14.11) |
называется многочленом Тейлора (порядка n), формула (14.10) - формулой Тейлора (порядка n) для функции f(x) в точке x = x0, а функция
|
rn(x) = f(x) - Pn(x) |
(14.12) |
- остаточным членом (порядка n) формулы Тейлора, а его представление в виде (14.2), т. е.
rn(x)
= o((x - x0)n),
x![]() x0,
x0,
- записью остаточного члена в виде Пеано.
Частный случай формулы Тейлора (14.10) при x0 = 0 называется формулой Маклорена
|
|
(14.13) |
где, согласно (14.2), остаточный член rn(x) можно записать в виде
|
rn(x)
= o(x)n,
x |
(14.14) |
Из
нижеследующей теоремы будет следовать,
что многочлен Тейлора единствен в своем
роде. Именно, никакой другой многочлен
не приближает функцию, заданную в
окрестности точки x0 с
точностью до бесконечно малых того же
порядка относительно x - x0, x![]() x0,
что и многочлен Тейлора.
Предварительно отметим, что любой
многочлен Pn(x)
=
x0,
что и многочлен Тейлора.
Предварительно отметим, что любой
многочлен Pn(x)
=  степени n для
любого x0 может
быть записан в виде Pn(x)
=
степени n для
любого x0 может
быть записан в виде Pn(x)
=  .
Действительно, положив h = x - x0,
использовав формулу бинома Ньютона и
собрав члены с одинаковыми степенями h,
получим
.
Действительно, положив h = x - x0,
использовав формулу бинома Ньютона и
собрав члены с одинаковыми степенями h,
получим
Pn(x)
= 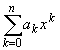

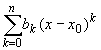 ,
,
где bk - некоторые постоянные.
Теорема 2. Если функция f(x) задана в окрестности точки x0 и имеет представление
|
f(x)
= |
(14.15) |
то
такое представление единственно.
![]() Пусть
наряду с представлением (14.15) имеет место
представление
Пусть
наряду с представлением (14.15) имеет место
представление
|
f(x)
= |
(14.16) |
Тогда, положив
|
ck = bk - ak, k = 0, 1, ..., n, |
(14.17) |
и вычтя из равенства (14.16) равенство (14.15), получим
|
|
(14.18) |
Перейдя
в этом равенстве к пределу при x![]() x0,
получим c0 = 0.
Заметим, что o((x - x0)m)
=
x0,
получим c0 = 0.
Заметим, что o((x - x0)m)
= ![]() (x)(x - x0)m,
(x)(x - x0)m, ![]()
![]() (x)
= 0, и, следовательно, при x
(x)
= 0, и, следовательно, при x![]() x0, m = 1,
2, ...
x0, m = 1,
2, ...
o((x - x0)m)/
(x - x0)
= ![]() (x)(x - x0)m-1 =
o((x - x0)m-1),
x
(x)(x - x0)m-1 =
o((x - x0)m-1),
x![]() x0.
x0.
Сократив
на x - x0, x![]() x0,
левую часть равенства (14.18) (в нем, как
уже доказано, c0 = 0),
получим
x0,
левую часть равенства (14.18) (в нем, как
уже доказано, c0 = 0),
получим
 + o((x - x0)n-1)
= 0,
x
+ o((x - x0)n-1)
= 0,
x![]() x0.
x0.
Перейдя
в этом равенстве к пределу при x![]() x0, x
x0, x![]() x0,
получим c1 = 0.
Продолжая этот процесс после m-го
шага, 0 < m < n,
получим
x0,
получим c1 = 0.
Продолжая этот процесс после m-го
шага, 0 < m < n,
получим
 + o((x - x0)n-m)
= 0,
x
+ o((x - x0)n-m)
= 0,
x![]() x0.
x0.
отсюда
при x![]() x0 следует,
что cm = 0, m = 0,
1, ..., n.
Таким образом, в силу равенств (14.17)
x0 следует,
что cm = 0, m = 0,
1, ..., n.
Таким образом, в силу равенств (14.17)
ak = bk,
m = 0,
1, ..., n. ![]()
Теорема 2 называется обычно теоремой единственности. Из нее следует, что если для n раз дифференцируемой в точке функции f получено представление ее в виде (14.15), то это представление является ее разложением по формуле Тейлора. В самом деле, при сделанных предположениях, согласно теореме 1, такое представление существует, а другого в силу теоремы 2 нет.



 +
o((x - x0)n),
x
+
o((x - x0)n),
x +
o((x - x0)n),
x
+
o((x - x0)n),
x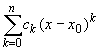 +
o((x - x0)n)
= 0,
x
+
o((x - x0)n)
= 0,
x