матан отвты / теория / 28

Теорема Лапласа и свойства определителей.

Пусть A – квадратная матрица n-го порядка.

Определитель k-го порядка, составленный из элементов матрицы A, расположенных на пересечении строк с номерами i1 , i2 , ..., ik и столбцов с номерами j1 , j2 , ..., jk , называется минором M k-го порядка матрицы A.

Если из матрицы A вычеркнуть строки и столбцы с такими номерами, то определитель n–k-го порядка полученной матрицы называется дополнительным минором для минора M

Обозначим символом S сумму индексов, нумерующих строки и столбцы такого минора:

S = i1 + j1 + i2 + j2 + ... + ik + jk .

Алгебраическим дополнением минора M называется дополнительный минор для минора M, умноженный на (–1)S.

Отметим, что алгебраическое дополнение Ai j элемента ai j (минора первого порядка) является частным случаем алгебраического дополнения минора.

Теорема Лапласа. Пусть D – определитель n-го порядка, в котором произвольно выбраны k строк (или столбцов), где 1 ≤k ≤ n – 1.

Тогда определитель D равен сумме произведений всех миноров k-го порядка, расположенных в выбранных строках (или столбцах), на их алгебраические дополнения.

1. Определитель транспонированной матрицы равен определителю исходной матрицы:

Это свойство вытекает из определения детерминанта и выражает равноправие строк и столбцов определителя.

2. Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножению определителя на это число:

.

Такое свойство определителей позволяет, в частности, выносить общий множитель элементов строки или столбца за знак определителя.

3. Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

.

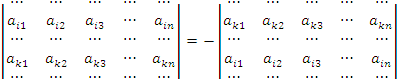4. Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю:

.

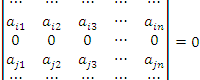5. Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю:

6. Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю:

.

7. Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

.

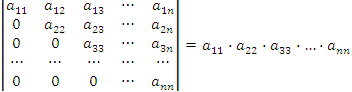8. Если все элементы k-ой строки (столбца) определителя представлены в виде сумм  a_k j + b_k j, то определитель можно представить в виде суммы соответствующих определителей:

  .

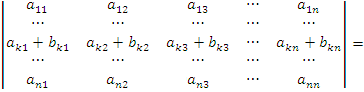
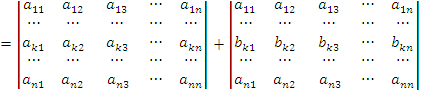9. Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число:

 

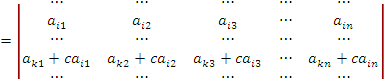
10. Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей: 

Асимптоты. Общая схема построения графика функции.