
матан отвты / теория / 20-25
.docxБилет 20
-
Сравнение функций.







-
Уравнения прямой на плоскости. Взаимное расположение прямых на плоскости (параллельность и перпендикулярность).
Каждая прямая на плоскости определяется линейным уравнением первой степени с двумя неизвестными.
-
Уравнение прямой с угловым коэффициентом имеет вид:
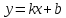
-
Общее уравнение прямой:
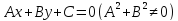
-
Уравнение прямой в отрезках:
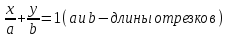
-
Уравнение прямой, проходящей через данную точку в данном направлении:
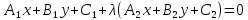
-
Уравнение прямой, проходящей через две данные точки:

-
Нормальное уравнение прямой:

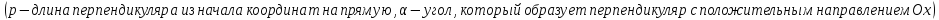
-
Уравнение прямой в полярных координатах:
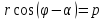
Если прямые заданы уравнениями с угловыми коэффициентами.
Условие
параллельности прямых – равенство
угловых коэффициентов
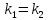
Условие
перпендикулярности -

Если прямые заданы общими уравнениями.
Условие
их параллельности -
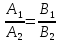 .
.
Условие
перпендикулярности -
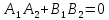
Билет 21
-
Производная и дифференциал функции. Уравнение касательной прямой.
Пусть
функция
 определена на некоторой окрестности
точки
определена на некоторой окрестности
точки
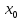 и пусть x
– некоторая точка этой окрестности.
Если отношение
и пусть x
– некоторая точка этой окрестности.
Если отношение
 имеет предел при
имеет предел при
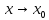 ,
то этот предел называется производной
функции в точке
,
то этот предел называется производной
функции в точке
 и обозначается
и обозначается
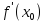 :
:

Пусть
функция
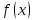 определена на некоторой окрестности
точки
определена на некоторой окрестности
точки
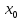 ,
если ее приращение в этой точке
,
если ее приращение в этой точке
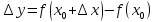 ,
,
 представимо в виде
представимо в виде
 ,
где А – постоянная (при фиксированной
точке
,
где А – постоянная (при фиксированной
точке
 А есть некоторое число, не зависящее от
А есть некоторое число, не зависящее от
 ;
конечно, при изменении точки
;
конечно, при изменении точки
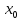 число А, вообще говоря, меняется) и
число А, вообще говоря, меняется) и
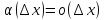 при
при
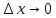 .
Линейная функция
.
Линейная функция
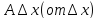 дифференциалом функции y=f(x),
в точке
дифференциалом функции y=f(x),
в точке
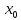 и обозначается df(
и обозначается df(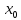 )
или, короче, dy.
)
или, короче, dy.
Уравнение касательной прямой.
Пусть
функция y=f(x)
непрерывна при
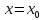 .
В точке
.
В точке
 существует наклонная касательная к
графику функции y=f(x)
тогда и только тогда, когда функция
y=f(x)
имеет в точке
существует наклонная касательная к
графику функции y=f(x)
тогда и только тогда, когда функция
y=f(x)
имеет в точке
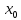 производную. При этом уравнение
касательной будет иметь вид
производную. При этом уравнение
касательной будет иметь вид
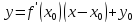 ,
где
,
где
 ,
и, значит, производная в точке
,
и, значит, производная в точке
 равна тангенсу угла наклона касательной
к оси Ox,
а дифференциал в точке
равна тангенсу угла наклона касательной
к оси Ox,
а дифференциал в точке
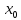 равен приращению ординаты касательной.
равен приращению ординаты касательной.
-
Смешанное произведение векторов и его свойства.
Под смешанным произведением векторов a, b и c понимается число abc=(axb)*c.
Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку.
Свойства:
-
Смешанное произведение не меняется при циклической перестановке его сомножителей. abc=bca=cab
-
При перестановке двух соседних сомножителей смешанное произведение меняет знак на обратный. bac=acb=cba= -abc
Билет 22
-
Правила вычисления производных, связанные с арифметическими действиями над функциями.
Правила вычисления производных, связанные с арифметическими действиями над функциями.


-
Векторное произведение векторов и его свойства.
Под векторным произведением двух векторов понимается вектор, для которого:
-
Модуль равен площади параллелограмма, построенного на векторах.
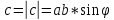
-
Этот вектор перпендикулярен перемножаемым векторам.
-
Направление этого вектора определяется по правилу правого винта.
Свойства:
-
Не обладает коммутативным свойством. При изменении порядка сомножителей, произведение меняет знак на противоположный, сохраняя модуль.
-
Векторный квадрат равен нулевому вектору.
-
Скалярный множитель можно выносить за знак векторного произведения.
(kAxB)=(AxkB)=k(AxB)
-
Обладает векторным свойством.
(A+B)xC=(AxC)+(AxB)
Билет 23
-
Производная сложной и обратной функции. Вычисление производной для функций, заданных неявно и параметрически.
Производная обратной фунции

Производная сложной фунции

Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.Производная неявной функции выражается через аргумент х и функцию у.
Например
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2 у'-3(1 у+х у')=0
следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х).
Параметрически заданная ф.
Предположим,
что функциональная зависимость ![]() от
от ![]() не
задана непосредственно
не
задана непосредственно ![]() ,
а через промежуточную величину —
,
а через промежуточную величину — ![]() .
Тогда формулы
.
Тогда формулы
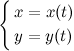
задают параметрическое представление функции одной переменной.
Пусть
функция ![]() задана
в параметрической форме, то есть в виде:
задана
в параметрической форме, то есть в виде:
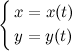
где
функции ![]() и
и ![]() определены
и непрерывны на некотором интервале
изменения параметра
определены
и непрерывны на некотором интервале
изменения параметра ![]() .
Найдем дифференциалы от правых и левых
частей каждого из равенств:
.
Найдем дифференциалы от правых и левых
частей каждого из равенств:
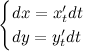
Далее,
разделив второе уравнение на первое, и
с учетом того, что ![]() ,
получим выражение для первой производной
функции, заданной параметрически:
,
получим выражение для первой производной
функции, заданной параметрически:
![]()
Для
нахождения второй производной ![]() выполним
следующие преобразования:
выполним
следующие преобразования:
![]()
-
Скалярное произведение векторов и его свойства.
Под
скалярным произведением двух векторов
понимается число, равное произведению
длин этих векторов на косинус угла между
ними.
Скалярное произведение векторов равно сумме попарных произведений их одноименных координат.
Геометрический смысл – скалярное произведение двух векторов равно длине одного из них, умноженной на проекцию другого на ось с направлением первого.
Физический смысл – работа постоянной силы при перемещении ее точки приложения.
Свойства:
-
ab=ba – коммутативность.
-
(a+b)*c=a*c+b*c – ассоциативность.
-
a^2=|a|^2 – скалярный квадрат вектора равен квадрату модуля этого вектора (угол равен 0).
-
(ka, b)=(a, kb)=k(a, b), k – скаляр. Скалярный множитель можно выносить за знак скалярного произведения.
-
(ka+lb, c)= k(a, c)+l(b, c), k и l – скаляры. Скалярное произведение линейной комбинации векторов на произвольный вектор равно такой же линейной комбинации данных векторов на этот вектор.
Билет 24
-
Производные высших порядков. Теорема о высших производных суммы и произведения функций.
Пусть
функция f(x),
определенная на интервале (a,
b),
в каждой точке
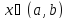 имеет производную f’(x)
и пусть
имеет производную f’(x)
и пусть
 .
Производная функции f’(x)
в точке
.
Производная функции f’(x)
в точке
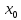 называется второй производной y=f(x)
и обозначается f’’(
называется второй производной y=f(x)
и обозначается f’’(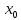 ).
).
Теорема о высших производных суммы и произведения функции.
Пусть
функции
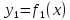 и
и
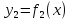 имеют производные n-го
порядка в точке
имеют производные n-го
порядка в точке
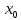 тогда функции
тогда функции
 и
и
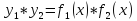 также имеют производные n-го
порядка в точке
также имеют производные n-го
порядка в точке
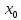 причем
причем
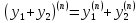 (*),
(*),
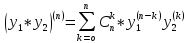 (**)
– формула Лейбница
(**)
– формула Лейбница
Где
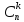 обозначает число сочетаний из n
элементов k,
k=0,
1, 2…
обозначает число сочетаний из n
элементов k,
k=0,
1, 2…
Доказательство.
Лекция
12 слайд 24.



-
Понятие вектора, его геометрическое и аналитическое представление. Действия над векторами (сложение, умножение вектора на число) и их свойства.
Величина, кроме числового значения характеризуемая еще и направлением, называется вектором (Аналитическое представление). Вектором называется упорядоченная пара точек. (Геометрическое представление).
Вектор характеризуется длиной и направлением.
Действия над векторами:
Сложение. Суммой нескольких векторов, например, a b c d называется вектор s=a+b+c+d, по величине и направлению равный замыкающей ломаной линии, построенной на этих векторах. Правило треугольника, правило параллелограмма. Модуль суммы двух векторов не превышает суммы модулей этих векторов.
Умножение вектора на число. Произведением вектора a на скаляр k называется вектор b=ak=ka, имеющий длину b=|k|a, направление, которго: 1. Совпадает с направлением вектора a, если k>0; 2. Противоположно ему, при k<0; 3. Произвольно, если k=0.
Свойства:
1: ~a +~b = ~b +~a;
2: (~a +~b) +~c = ~a + (~b +~c);
3: ~a +~o = ~a;
4: ~a + (-~a) = ~o;
5: (kl)*~a = k(l*~a);
6: (k+l)*~a = k*a+l*~a;
7: k*(~a +~b)=k*~a+k*~b;
8: 1* ~a = ~a:
Билет 25
-
Вычисление производных высших порядков для сложных функций, обратных функций и функций, заданных параметрически.




-
Матрицы и их применения. Сложение матриц и умножение матрицы на число, их свойства.
Матрица – математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся элементы. Матрицы широко применяются в математике для компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный аппарат позволяет свести решение СЛАУ к операциям над матрицами.
Сложение
матриц. Суммой матриц
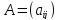 и B
и B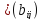 одинакового размера называется матрица
C
одинакового размера называется матрица
C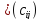 того же размера, причем
того же размера, причем
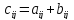 .
.
Свойства: Коммутативность (A+B=B+A), Ассоциативность ((A+B)+C=A+(B+C))
Произведением
матрицы
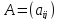 на число λ называется матрица
на число λ называется матрица
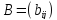 того же размера, что и матрица А, причем
того же размера, что и матрица А, причем
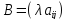 .
.
Свойства: Ассоциативность (λ(μA)=(μλ)A), дистрибутивность относительно сложения матриц(λ(A+B)=λA+λB), дистрибутивность относительно сложения чисел ((λ+μ)A=λA+μA)
