
матан отвты / теория / 27
.doc
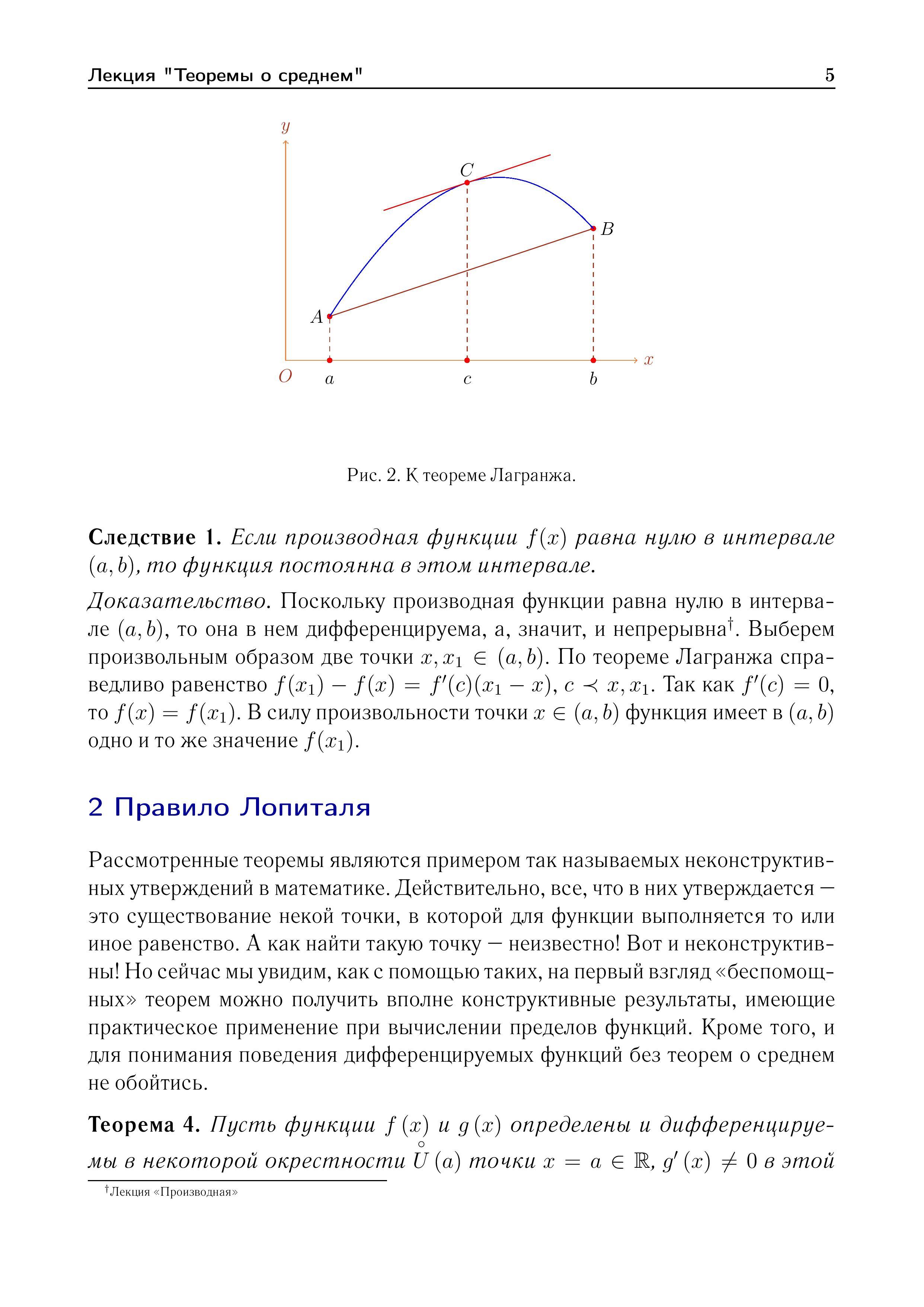
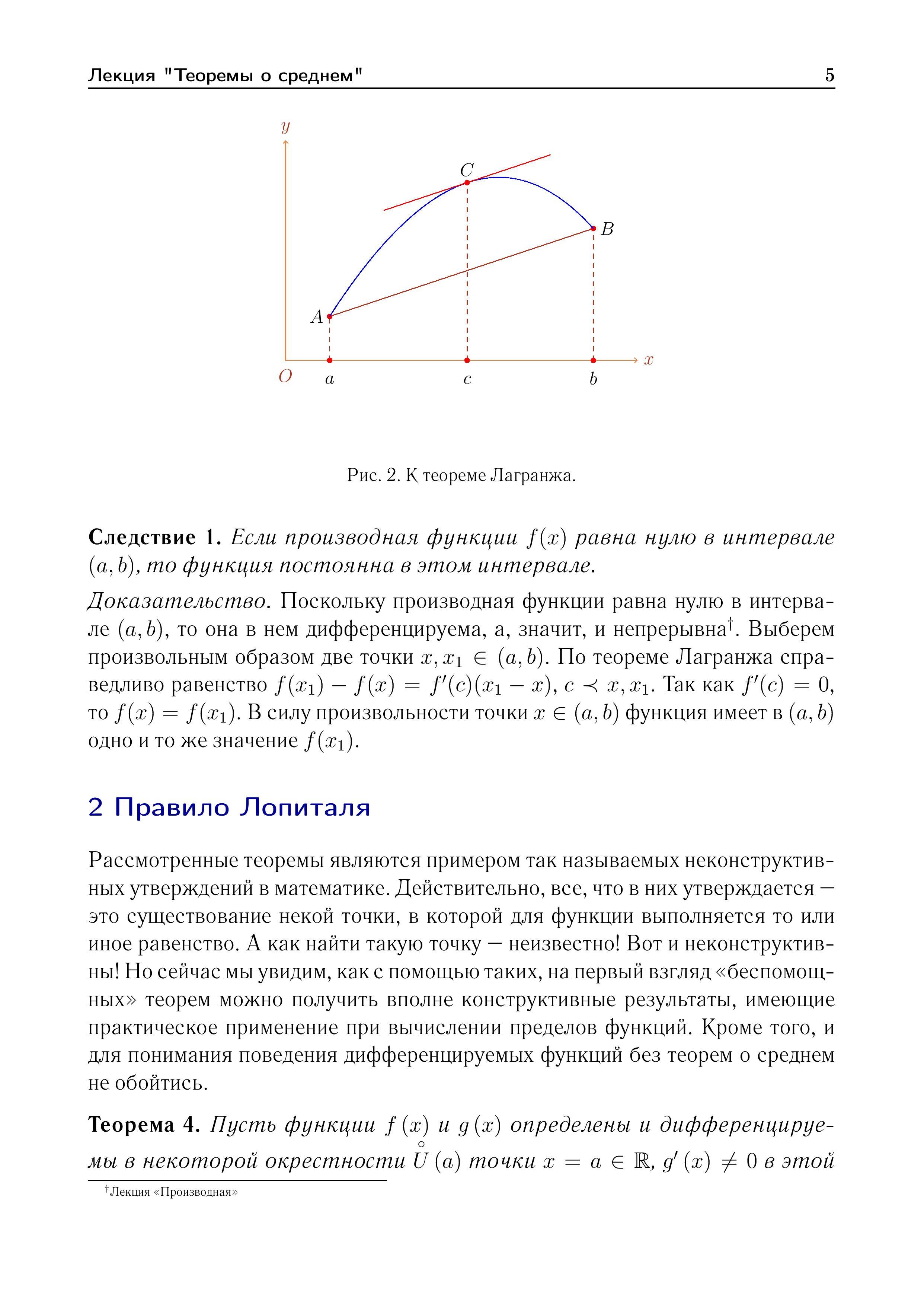
Теоремы
Лагранжа и Коши.



Присоединенная и обратная матрицы. Их свойства.
А
– квадратная матрица. Квадратная матрица
![]() того же порядка, что и А, называется
присоединенной по отношению к А, если
каждый ее элемент
того же порядка, что и А, называется
присоединенной по отношению к А, если
каждый ее элемент
![]() равен алгебраическому дополнению
элемента
равен алгебраическому дополнению
элемента
![]() матрицы А
матрицы А
![]()
|
Присоединенная матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов исходной матрицы. |

Исходная матрица:

Где:
-
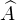 —
присоединённая(союзная,
взаимная) матрица;
—
присоединённая(союзная,
взаимная) матрица; -
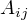 —
алгебраические
дополнения исходной матрицы;
—
алгебраические
дополнения исходной матрицы; -
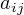 —
элементы
исходной матрицы.
—
элементы
исходной матрицы.
Алгебраическим
дополнением элемента ![]() матрицы
матрицы ![]() называется
число
называется
число
![]() ,
,
где ![]() —
дополнительный минор, определитель
матрицы, получающейся из исходной
матрицы
—
дополнительный минор, определитель
матрицы, получающейся из исходной
матрицы ![]() путем
вычёркивания i -й
строки и j -го
столбца.
путем
вычёркивания i -й
строки и j -го
столбца.
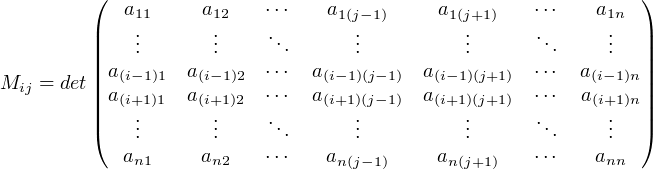
Алгоритм получения обратной матрицы
-
заменить каждый элемент исходной матрицы на его алгебраическое дополнение - в результате будет получена присоединенная матрица
-
разделить каждый элемент транспонированной присоединенной матрицы на определитель исходной матрицы.
![]()
А*АТ=АТ*А=detA*E, где Е – единичная матрица того же порядка, что и А.
Присоединенная матрица является квадратной из определения, так как алгебраические дополнения вводятся только для квадратных матриц
Пусть А – квадратная матрица. Квадратная матрица А-1 того же порядка, что и А, называется обратной по отношению к А, если А-1А=АА-1=Е
Для невырожденной матрицы А существует обратная матрица, которая может быть вычислена по формуле
![]()
Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
