12_Шишкина Л.П., Бояринцева Т.П., Сержант Т.Н_Лаб_практикум по информатике_VBA_2012

VBA6. Создание приложения для вычисления многочленов

.

Вычислить многочлен пятой степени

f(x) a0x5 a1x4 a2x3 a3x2 a4x a5,

используя для вычислений экономичный алгоритм Герона:

f(x) ((((a0x a1)x a2 )x a3)x a4 )x a5 .

1.На свободном рабочем листе создать командную кнопку с надписью Вычисление многочлена. В программный код кнопки вписать инструкцию UserForm1.Show.

2.Для добавления к проекту новой формы в окне редактора Visual Basic выполнить команду

Вставка/UserForm.

3.Добавить необходимые элементы управления, используя панель элементов (см.рис.).

4.Оставаясь в редакторе Visual Basic, двойным щелчком левой кнопки мыши по форме вызвать ее программный код и перейти к разработке модуля.

Сначала опишите массив А, отведенный под коэффициенты многочлена, переменные x и S, не забывая о комментариях.

Dim A(5) ‘ массив для коэффициентов многочлена

Dim x ‘ переменная для значения аргумента

Dim S ‘ переменная для вычисленного значения многочлена.

Затем надо написать процедуры, назначенные полям ввода коэффициентов и аргумента.

31

Необходимо также написать событийную процедуру для кнопки Выход:

Кнопке Вычислить, имеющей имя Next_Button_Click( ), назначим следующую процедуру:

Private Sub Next_Button_Click() ' вычисление по схеме Горнера

Предложенная форма может быть использована и при вычислении многочленов степени меньше пятой, если в соответствующие поля вводить нулевые значения коэффициентов. Возвратившись в Excel и щелкнув по командной кнопке Вычисление многочлена, протестируем созданную форму, вычисляя следующие многочлены:

1)

3)f (x) 0.456078x 0.456078, x 0

Тестирование можно проводить и оставаясь в редакторе VBA (см. раздел 7 «Отладка приложений»).

VBA7. Сортировка чисел в столбце по возрастанию или убыванию с созданием формы и панели инструментов с кнопкой

В предыдущих работах, посвященных созданию формы, запуск программы выполнялся с помощью кнопки размещенной на листе Excel. Целью этой работы является создание панели инструментов с кнопкой для выполнения программы.

1. Создайте панель инструментов и разместите на ней кнопку. Панель инструментов должна появляться при открытии рабочей книги. В окне редактора Visual Basic выберите лист ThisWorkBook и включите в него следующие две процедуры:

1) Процедура создания новой панели инструментов при открытии рабочей книги

Private Sub Workbook_WindowActivate(ByVal Wn As Excel.Window) 'Создание новой панели инструментов

With Application.CommandBars.Add(Name:="Моя панель инструментов", _ Position:=msoBarTop, MenuBar:=False, Temporary:=True)

.Visible = True

With .Controls

'Создание кнопки с надписью

With .Add(Type:=msoControlButton, Id:=1) 'добавить кнопку на панель инструментов

.Caption = "Сортировка" 'надпись на кнопке

.TooltipText = "Сортировка" 'всплывающая подсказка

.Style = msoButtonCaption

.OnAction = "Sort" 'при нажатии на кнопку выполняется процедура

End With

32

End With

End With

End Sub

2) Процедура, удаления созданной панели инструментов при закрытии приложения

Private Sub Workbook_WindowDeactivate(ByVal Wn As Excel.Window) With Application

.CommandBars("Моя панель инструментов").Delete End With

End Sub

В результате будет создана панель инструментов с кнопкой Сортировка (см. Рис).

2.Добавьте модуль через пункт меню Вставка/Модуль и введите процедуру Sort для отображения формы на экране.

Sub Sort() UserForm1.Show End Sub

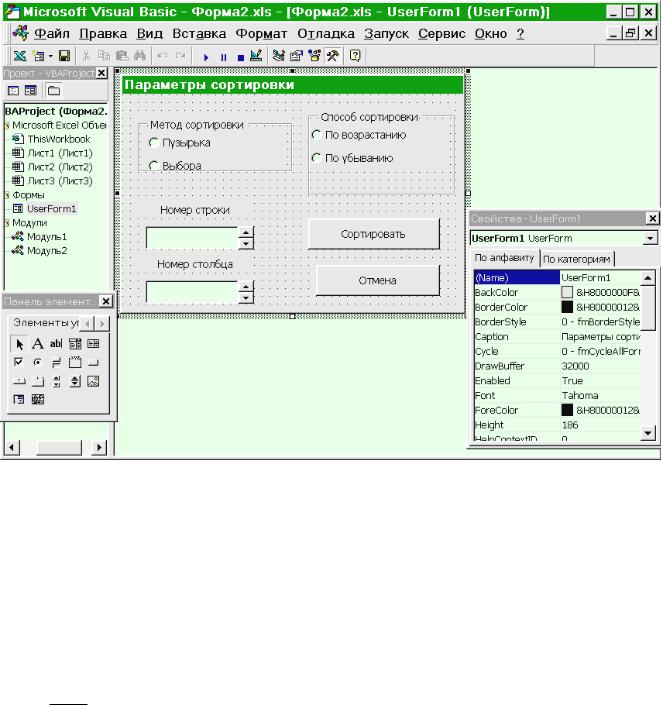
3.В окне редактора создайте форму, разместите на ней требуемые элементы управления и установите свойства (см. Рис. на следующей стр.).

4.Напишите процедуры, связанные с формой, а также процедуру UserForm_Initialize (задание значений по умолчанию).

Private Sub UserForm_Initialize() ' Процедура инициализации формы OB1.Value = True

OptionButton1.Value = True SB1.Min = 1

SB1.Max = 100 TB1.Value = SB1.Value SB2.Min = 1

33

SB2.Max = 100

TB2.Value = SB2.Value

End Sub

5. Напишите процедуры сортировки. Сортировка выбором заключается в том, что требуется найти элемент массива, имеющий наименьшее значение и переставить его с первым элементом, затем проделать то же самое, начав со второго элемента.

9. Самостоятельные и контрольные задания

Задание 1

1)Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа, если это не так.

2)Пусть x1=y1=1; xi=0.3xi-1; yi=xi-1+yi-1, i=2,3,… Дано натуральное n. Найти

n xi i 1 1 yi

3)Даны целые числа а1, а2, а3. Получить целочисленную матрицу [bij] i, j=1,2,3, для которой bij=ai-3aj.

Задание 2

1)Даны 3 действительных числа a, b, c (a 0). Полностью исследовать квадратное уравнение ax2+bx+c=0, т.е. если действительных корней нет, то должно быть выведено сообщение об

этом, иначе должны быть найдены и помещены в текстовые поля 2 корня. 2) Пусть a0=1; ak=kak-1+1/k; k=2,3,… Дано натуральное n. Получить an.

34

3)Дана действительная матрица размера m x n. Определить числа b1,b2,…,bm, равные соответственно:

а) суммам элементов строк; б) произведением элементов строк;

в) наименьшим значениям элементов строк; г) значениям средних арифметических элементов строк;

д) разностям наибольших и наименьших значений элементов строк.

Задание 3

1. Даны действительных числа x, y. Вычислить z: x-y, если x>y

z =

y-x+1 в противном случае. 2. Пусть v1=v2=0; v3=1.5;

3.Дана действительная квадратная матрица порядка 10. В строках с отрицательным элементом на главной диагонали найти:

а) сумму всех элементов; б) наибольший из всех элементов.

Указать количество учтенных слагаемых.

Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше, чем . Это и все последующие слагаемые можно уже не учитывать.

Задание 5

1)«Тестирование коллектива». Пусть целочисленная матрица размера nxm содержит информацию об учениках некоторого класса из n человек: j-я строка содержит информацию о i-м ученике. В первом столбце проставлен возраст в годах, во втором – рост в см, в третьем – успеваемость (округленный средний балл) и т. д. Ученик называется среднестатистическим по k-му параметру (уникальным по k-му параметру), если на нем достигается минимум (максимум) модуля разности среднего арифметического чисел из k-го столбца и значения k-го параметра этого ученика. По матрице указанного вида определить номера учеников:

а) самых уникальных, б) самых средних.

2)Элемент матрицы называется седловой точкой, если он является одновременно наименьшим в своей строке и наибольшим в своем столбце. Дана действительная матрица размера 5x 6.

35

Выяснить, имеются ли седловые точки в этой матрице, и если они имеются, то указать индексы одной из них.

Задание 6

Найти количество различных чисел в произвольном одномерном массиве чисел, который предварительно разместить на рабочем листе книги Excel.

Создать диалоговое окно (UserForm), содержащее командную кнопку, а в событийной процедуре, соответствующей нажатию кнопки, определить это количество. Полученное значение вывести в поле с надписью Количество различных чисел.

Задание 7

Найти количество совпадающих чисел в произвольном одномерном массиве чисел, который предварительно разместить на рабочем листе книги Excel.

Создать диалоговое окно (UserForm), содержащее командную кнопку, а в событийной процедуре, соответствующей нажатию кнопки, определить это количество. Полученное значение вывести в поле с надписью Количество совпадающих чисел.

Задание 8

Найти наибольшее число в произвольном одномерном массиве чисел, который предварительно разместить на рабочем листе книги Excel.

Создать диалоговое окно (UserForm), содержащее командную кнопку, а в событийной процедуре, соответствующей нажатию кнопки, определить наибольшее число массива. Полученное значение вывести в поле с надписью Наибольшее число.

Курсовые работы

Общие требования и рекомендации

Курсовая работа должна включать в себя текст на Word и программу на VBA в книге

Excel.

Текст работы - это теоретическая часть, которая должна содержать титульный лист, описание постановки задачи, алгоритма ее решения, например, алгоритма и последовательности вычисления координат теодолитного хода с указанием формул, а также описание программы - ее основных блоков и результатов отладки на примере.

Программа - это практическая часть курсовой работы. Для ее разработки надо создать интерфейс пользователя, написать событийные и общие процедуры и отладить приложение на примерах.

1.Разработка приложения “Решение системы линейных уравнений”

1.Взять за основу модуль, созданный в лабораторной работе 3. Модуль должен содержать следующие общие процедуры:

MNTab - определение M, N - размерности матрицы,

TabCXCY - копирование идентификаторов столбцов и строк в массивы CX, CY, TabA - копирование матрицы с листа Excel в массив A,

XAI (I) - вычисление скалярного произведения вектора x на вектор aI (функция) с записью результата в I-ю ячейку первого столбца на листе Excel,

Jordan - шаг жорданова исключения (процедура поясняется ниже) – преобразование всей матрицы A с записью новых значений ее элементов в таблицу на листе Excel, обращение к процедуре TabA, перемена местами элементов CX и CY с записью значений и в ячейки Excel, копирование матрицы с листа Excel в массив A.

36

2.Разместить на листе Excel командную кнопку BTN1 с надписью (свойство Caption)

Решение системы уравнений.

3.В событийную процедуру BTN1_Click включить:

-определение M, N, вывод сообщения и завершение работы, если M не равно N;

-переопределение размерности массивов CX, CY, A и копирование в них содержимого соответствующих ячеек листа Excel;

-выполнение шага жорданова исключения N раз (r – номер диагонального элемента матрицы, называемого разрешающим; с ним выполняется шаг жорданова исключения); перед обращением к процедуре Jordan надо проверять, не равен ли нулю элемент матрицы A(r,r) – этот фрагмент программы можно записать так

For r = 1 To N

If Abs(A(r, r)) < 0.00000001 Then

MsgBox "Матрица содержит линейно зависимые строки (столбцы)": Exit Sub End If

Jordan r Next r

(проверка на нуль в программах выполняется с учетом точности вычислений);

-вычисление каждого значения Xi (i=1,…,N) путем умножения вектора y на вектор Ai с

использованием функции XAI; заметим, что после того, как были выполнены N шагов жордановых исключений, на месте матрицы A находится обратная матрица A-1, а массивы CX и CY поменялись своим содержимым – в массиве CX теперь хранятся известные значения Yj (j=1,…,N), а в массиве CY (и в первом столбце на листе Excel) – идентификаторы X1,…,XN. Эти идентификаторы и надо заменить вычисленными

значениями Xi (i=1,…,N).

Поясним алгоритм шага жорданова исключения. В разделе 4 упоминалось, что матрицу A (см. рис. 2) можно рассматривать как таблицу коэффициентов, позволяющих связать любой Yi уравнением со значениями X1 ,…, XN : Yi = x ∙ Ai. Глядя на эту таблицу, над столбиками представим себе значения Xj (вектор-строку x), а левее строк – значения Yi (вектор-столбец y). Один шаг жорданова исключения с разрешающим элементом Arr приводит к тому, что Xr и Yr меняются местами, а вся матрица A изменяется так:

-разрешающий элемент A(r,r)=1/A(r,r) ,

-прочие элементы A(i,j) = ( A(i,j) ∙ A(r,r) – A(i,r) ∙ A(r,j) ) / A(r,r) .

После того, как будут выполнены N шагов жордановых исключений, вектор y окажется наверху (над матрицей), а вектор x – слева от матрицы. Сама матрица к этому моменту будет обращена

– теперь она содержит коэффициенты, позволяющие вычислять значения Xi , если известны значения Yj : X(i)= y ∙ Ai.

Приложение надо отладить на примерах. Подготовить примеры совсем не трудно.

Представим себе, что N=3, а значения элементов вектора x известны, например: x={1,2,3}. Теперь, задавшись матрицей A, например, A={11,13,13; 21,22,24; 30,32,33}, получим y={76, 137, 193}. Неизвестными будем считать значения X1=1, X2=2, X3=3. Их и найдем.

Литература к курсовой работе 1. Зуховицкий С.И., Авдеева Л.И. Линейное и выпуклое программирование. М: Наука, 1967. –460 с.

2. Разработка приложения “Статистический анализ данных”

Постановку задачи для этого приложения ограничим упрощенным статистическим анализом: вычислением средних значений признаков, стандартов (средне-квадратических отклонений от генерального среднего), матрицы коэффициентов корреляции и матрицы стандартов коэффициентов корреляции. Поясним эту задачу, обратившись к матрице на рис. 10.5. Теперь матрицу будем рассматривать не как таблицу коэффициентов, связывающих

37

зависимые переменные y={Y1,…,YN} c независимыми переменными x={X1,…,XN} (см. предыдущую работу), а как таблицу объекты-свойства. Соответственно, в первом столбце листа Excel разместим идентификаторы объектов (например, их номера: 1 ,…, M), а в первой строке – идентификаторы свойств (например, X1 ,…, XN). Одна строка матрицы содержит значения свойств одного объекта, а один столбец – значения одного свойства для всех объектов.

Таблицы объекты-свойства часто применяются в различных предметных областях. Например, в геологии при поисках и разведке полезных ископаемых отбирают из массива горных пород M проб, а в каждой пробе химическими или физическими методами определяют содержания N компонентов (обычно M>N). По этим анализам судят о массиве горной породы. Аналогично тестируют продукцию металлургического комбината – выборочно отбирают образцы и подвергают их анализам на содержание железа, серы и других элементов. Статистически обработав результаты анализов образцов, судят о качестве целой партии продукции. Здесь важно понять, что в подобных ситуациях практически невозможно проанализировать весь массив горных пород или всю партию продукции - как говорят статистики, всю генеральную совокупность. Поэтому в таблицу объекты-свойства включают результаты анализов (измерений) для выборки из генеральной совокупности. По этой выборке находят средние значения Xjo каждого признака, характеризующие центр рассеяния значений признака и коэффициенты ковариации Sjk, характеризующие меру и форму рассеяния:

Коэффициент ковариации Sjk вычисляется так: берутся два столбца матрицы с номерами j и k , затем суммируются произведения отклонений i-ых элементов этих столбцов от своих средних, и накопленная сумма делится на M, полученное среднее значение произведения отклонений умножается на поправочный коэффициент M / (M-1). Этот коэффициент компенсирует занижение коэффициентов ковариации, которое произошло, т.к. вместо неизвестных генеральных средних в формуле использованы выборочные средние значения признаков.

Рассчитанную матрицу коэффициентов ковариации можно разместить на листе 2 книги Excel – так же, как на листе 1 размещена исходная матрица (см. рис. 10.5), только размерность ковариационной матрицы не M ∙ N , а N ∙ N , и идентификаторами строк и столбцов являются идентификаторы признаков (свойств) объектов. Средние значения надо разместить на листе 1 под соответствующими столбцами исходной матрицы, но пропустив одну строку. На листе 1 надо также разместить командную кнопку BTNSTAT с надписью (свойство Caption) Расчет статистик. В начало событийной процедуры BTNSTAT_Click надо включить определение M, N, копирование в массив CX идентификаторов признаков, а в двумерный массив A – матрицы (см. предыдущую работу и модуль, приведенный в подразделе 10.4 после рис. 10.5). После копирования данных в массивы, запрограммируйте вычисление средних значений признаков и матрицы ковариаций.

Диагональные элементы ковариационной матрицы называются дисперсиями. Корни квадратные из дисперсий Sjj называются стандартами sj, или средне-квадратическими отклонениями значений признаков от генеральных средних (от математических ожиданий значений признаков). Стандарты надо вычислить и разместить на листе Excel под средними значениями.

Часто между признаками наблюдаются связи: при переходе от объекта к объекту мы видим, что увеличение признака j , как правило, сопровождается увеличением признака k – это положительная корреляция. Если же при увеличении значения Xj значение Xk, как правило, уменьшается, то это корреляция отрицательная. Близость связи между двумя признаками j и k к линейной оценивается коэффициентом парной корреляции:

rjk = Sjk / (sj ∙ sk) , j=1,…, N, k=1,…, N.

38

Матрицу коэффициентов корреляции можно разместить на месте ковариационной матрицы, нормируя ее элементы на стандарты. Значения коэффициентов парной корреляции должны принадлежать интервалу [-1, 1 ].

Достоверность, или, как говорят статистики, значимость коэффициентов корреляции зависит от объема выборки. Если в выборку включить малое число проб, а рассеяние значений Xj и Xk велико, то коэффициент корреляции случайно может получиться большим или малым. Чтобы оценить значимость коэффициентов парной корреляции, вычисляют их стандарты:

s(rjk)= ( 1- r2jk ) /M 1 , j=1,…, N, k=1,…, N.

Матрицу стандартов коэффициентов парной корреляции можно разместить на листе 3 книги Excel. С некоторым приближением о значимости коэффициентов корреляции судят так: если │ rjk │< s(rjk) , то корреляцию нельзя считать значимой.

При разработке рассматриваемого приложения наиболее трудным этапом является программирование вычисления коэффициента ковариации. Это вычисление целесообразно локализовать в функции

Function SJK ( j As Integer, k As Integer) As Double

К этой функции необходимо обратиться N∙N раз : цикл по j от 1 до N, а при каждом j цикл по k от 1 до N.

Методы статистического анализа данных полезно знать каждому специалисту. Эта курсовая работа знакомит с началами статистического анализа. Любознательные студенты могут, обратившись к литературе, расширить свои знания в этой области, а при желании – и само разработанное приложение, включив в него, например, вычисление коэффициентов асимметрии и эксцесса для каждого признака, коэффициентов уравнения регрессии, связывающего первый признак с остальными, и т.п.

Литература к курсовой работе 2.

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.:

Наука, 1968. –720 с.

Шор Я. Статистистические методы анализа и контроля качества и надежности. М.: Советское радио, 1962. –552 с.

Ломтадзе В.В. Программное и информационное обеспечение геофизических исследований. М.: Недра, 1993. –268 с.

3. Разработка приложения “Решение треугольника”

Пусть имеется треугольник ABC с углами A,B,C и длинами противолежащих углам сторон LA,LB,LC. Разработать приложение, в котором по заданным параметрам треугольника определяются остальные - не заданные. Если исходные данные заданы так, что задачу решить нельзя, то программа должна выводить сообщение с помощью процедуры MsgBox.

Рекомендации. Разместить на листе Excel рисунок треугольника с подписями вершин,

поля (TextBox) с именами TBA, TBB, TBC, TBLa, TBLb, TBLc и кнопку с заголовком

Вычислить. Слева от текстовых полей поместить подписи A,B,C, LA,LB,LC. Событийная процедура, соответствующая командной кнопке, должна проверять каждый параметр (задан ли он) и вычислять (если не задан) по значениям других параметров.

4. Разработка приложения “Определение площади произвольной фигуры”

Пусть многоугольник произвольной формы (полигон) задан координатами вершин X,Y в двух столбцах на листе Excel. На этом же листе разместить командную кнопку и поле (TextBox) с именем TBS для вывода значения площади. Слева от поля TBS поместить надпись Площадь полигона. Вычисление площади целесообразно локализовать в подпрограмме-функции вида

39

Function Spoligon(M As Integer, X() As Single, Y() As Single) As Single Dim i As Integer, x1 As Single, y1 As Single, S As Single

{ Вычисление S } End Function

Функция может содержать следующие блоки:

1)S=0, x1 = X(1), y1 = Y(1), i=2

2)S = S + (y1 * (X(i) - X(i + 1)) + Y(i) * (X(i + 1) - x1) + Y(i + 1) * (x1 - X(i))) / 2

3)i=i+1, передача управления блоку 2, если i<M

4)Spoligon = Abs(S)

5. Разработка приложений “Графические построения в плоскости XOY”

Различные графические построения часто необходимы в любой практической деятельности. В литературе по VBA этот вопрос практически не освещен, но в Excel и в Word всегда можно вызвать на экран панель инструментов Рисование и конструировать рисунок, включая в него линии, надписи и другие фигуры, образцы которых (Shapes) представлены на панели инструментов Рисование. Если перед созданием рисунка включить запись макроса (кнопка Записать макрос на панели инструментов Visual Basic), а затем в окне Visual Basic посмотреть его текст и, кроме того, обратиться к встроенной справке, то становится ясно, как программировать векторную графику в VBA. Именно так мы и поступили. Далее приводится начало модуля, содержащего базовые процедуры, с помощью которых можно программировать графические построения на плоскости XOY.

'Глобальные переменные и константы

Dim cx As Single, cy As Single

'cx,cy - масштабные коэффициенты: пиксели/сантиметры

Dim nx1 As Integer, ny1 As Integer, nx2 As Integer, ny2 As Integer

Dim RedClr As Integer, GreenClr As Integer, BlueClr As Integer

Dim FntName As String, FntSize As Integer, FntColor As Integer

Const nx0 As Integer = 25.5: Const ny0 As Integer = 25.5:

'Инициализация графического окна размером Lx ∙ Ly (в сантиметрах)

'Начало координат в левом верхнем углу окна, ось X направлена вправо, Y- вниз

Sub GrIni() SP 0, 0, 0

cx = TextBoxCX.Value: cy = TextBoxCY.Value Lx = TextBoxLX.Value: Ly = TextBoxLY.Value Лист2.Activate: Лист2.Shapes.SelectAll

Selection.Delete ' Удаление графических элементов с листа 2

Лист2.Shapes.AddShape(msoShapeRectangle, nx0, ny0, Lx * cx, Ly * cy).Select End Sub

' Пересчет координат из сантиметров чертежа в пиксели (точки) Function GETnx(xcm As Single) As Integer

GETnx = nx0 + xcm * cx End Function

Function GETny(ycm As Single) As Integer

GETny = ny0 + ycm * cy

End Function

' Перемещение в точку xcm, ycm (Move Absolute, координаты точки - в см) Sub MA(xcm As Single, ycm As Single)

nx1 = GETnx(xcm): ny1 = GETny(ycm) End Sub

40