12_Шишкина Л.П., Бояринцева Т.П., Сержант Т.Н_Лаб_практикум по информатике_VBA_2012

' Вычерчивание линии из текущей точки в точку xcm, ycm (Plot Absolute) Sub PA(xcm As Single, ycm As Single)

nx2 = GETnx(xcm): ny2 = GETny(ycm)

With Лист2.Shapes.AddLine(nx1, ny1, nx2, ny2).Line

.ForeColor.RGB = RGB(RedClr, GreenClr, BlueClr) End With

nx1 = nx2: ny1 = ny2 End Sub

'Установка цвета линий (Set Pen)

Sub SP(Red As Integer, Green As Integer, Blue As Integer)

RedClr = Red: GreenClr = Green: BlueClr = Blue

End Sub

'Установка шрифта, его размера и цвета (Set Font)

'Цвет: 1-черный, 2-пусто, 3-красный, 4- ярко-зеленый, 5-синий,

'6-желтый, 7-светло-фиол., 8-голубой, 9-коричн., 10-зеленый, 11-темно-синий

Sub SF(Name As String, Size As Integer, Color As Integer) FntName = Name: FntSize = Size: FntColor = Color

End Sub

'Надпись (Write String) – указываются размеры текстового окна и сам текст

Sub WS(xcm As Single, ycm As Single, Lxcm As Single, Lycm As Single, _ Txt As String)

Лист2.Shapes.AddTextbox(msoTextOrientationHorizontal, _ GETnx(xcm), GETny(ycm), Lxcm * cx, Lycm * cy).Select Selection.ShapeRange.Line.Visible = msoFalse Selection.Characters.Text = Txt

With Selection.Characters(Start:=1, Length:=Len(Txt)).Font

.Name = FntName

.Size = FntSize

.ColorIndex = FntColor End With

End Sub

'Значок (1-восьмиугольник, 2-звездочка, 3-треугольник)

Private Sub SignN(xcm As Single, ycm As Single, _

Lxcm As Single, Lycm As Single, NS As Integer) If NS = 1 Then Worksheets(2).Shapes.AddShape(msoShapeOctagon, _

(msoShapeIsoscelesTriangle, GETnx(xcm), GETny(ycm), Lxcm * cx, Lycm * cy).Select End Sub

Private Sub Btn1_Click() ' Пример событийной процедуры

GrIni

MA 5, 5

PA 10, 5

SP 200, 0, 0

PA 10, 10

SF "Times New Roman Cyr", 9, 11 WS -0.8, -0.2, 0.8, 0.4, "0.0"

End Sub

41

Предлагаемые процедуры разработаны нами, чтобы избежать непосредственного использования конструкций VBA, позволяющих размещать на листе книги Excel линии и надписи, поскольку синтаксис этих конструкций довольно сложен. Приведенный в конце модуля пример простейшей событийной процедуры показывает, как используя процедуры GrIni, MA, PA, SP, SF, WS, программировать построение графиков, схем, чертежей и т.п. Набор перечисленных процедур расчитан на то, что на листе 1 книги Excel размещены поля

TextBoxLX, TextBoxLY, TextBoxCX, TextBoxCY и командная кнопка Btn1.

В полях редактирования (TextBox) задаются размеры чертежа в см и масштабные коэффициенты для перехода от см к точкам (пикселям). Коэффициенты cx, cy можно скорректировать после вывода чертежа на принтер. Процедура GrIni должна использоваться первой – она вычерчивает прямоугольное окно размером Lx∙Ly на листе 2 книги Excel. В этом окне затем проводятся дальнейшие построения. Остальные процедуры легко понять по распечатке. Теперь сформулируем варианты курсовой работы.

Вариант 1. На листе 1 разместить элементы управления и в двух столбцах - значения X, Y. На листе 2 построить график Y(X). При построении координатных осей найти диапазоны изменения X, Y; оси оцифровать «круглыми» значениями.

Вариант 2. Аналогичен варианту 1, но надо строить график X(Y).

Вариант 3. Построить разными цветами графики F1(X), F2(X), разместив на листе 1 три ряда (столбца) чисел: X, F1, F2. Оба графика построить в одном и том же масштабе.

Вариант 4. Построить многоугольник (полигон) заданный координатами вершин X,Y в двух столбцах на листе Excel. Считать, что ось X направлена вверх (как принято в геодезии). Построить оси координат, оцифровав их "круглыми" значениями, нанести многоугольник, подписать порядковые номера точек.

6. Разработка приложения “Вычисление определенного интеграла”

Инженеру часто приходится вычислять значение определенного интеграла численными методами. Это бывает в тех случаях, когда либо не удается выразить интеграл в замкнутой форме, либо она настолько сложна , что проще воспользоваться численным интегрированием. Например, при проверке правильности выбора мощности двигателя по графику переходного процесса по току I(t) требуется в интервале от 0 до конечного времени работы tp вычислить

tp

интеграл t2(t)dt . Этот интеграл при произвольной кривой тока удобнее всего

0

вычислять численными методами параллельно с поиском решения дифференциальных уравнений, описывающих поведение системы электропривода.

В

Геометрический смысл определенного интеграла F(x)dx – это площадь

А

фигуры, ограниченной ординатами А и В, осью абцисс и графиком подинтегральной функции F(x) . Широко известными методами, использующими для приближенного подсчета определенных интегралов их замену конечной суммой, являются методы прямоугольников, трапеций, парабол (Симпсона).

Интегрирование по методу прямоугольников

42

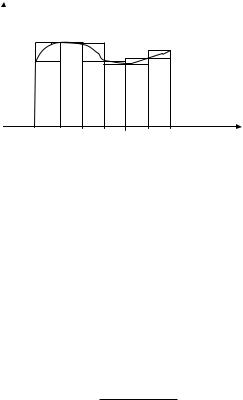
Метод прямоугольников основан на непосредственном определении интеграла:

b n 1

f (x)dx lim f ( ) xi ,

аi 0

[a,b] и некоторому выбору точек ξ0, ξ1, …,ξn-1, на отрезках разбиения.

Вычисление определенного интеграла геометрически сводится к вычислению площади

b

криволинейной трапеции, ограниченной I f (x)dxi функцией f(x), осью абсцисс и прямыми

a

x=a и x=b .

Если точку ξi совместить с левым концом отрезка xi , то приближенное значение интеграла равно площади фигуры и может быть представлено формулой левых

y

X0=a x1 xn-1 b=xn x

Если же в качестве ξi выбирать правый конец отрезка xi , то приближенное значение интеграла равно площади ступенчатой фигуры, ограниченной сверху пунктирной линией и считается по формуле правых прямоугольников:

Интегрирование по методу трапеций

Метод трапеций заключается в том , что на отрезке [a,b] дуга AB графика подинтегральной функции y=f(x) заменяется стягивающей ее хордой и вычисляется площадь трапеции Abba.

b

f (x)dx (b a) f (a) f (b),

2

a

Точность вычислений возрастает, если отрезок [a,b] разделить на несколько частей и применить формулу к каждому отрезку Δxi . Тогда

Так как под знаком суммы величины yi встречаются дважды (от i =1 до i =n-1), то последнее равенство можно записать в следующем виде:

43

эта формула называется общей формулой трапеций ее можно переписать в следующем виде:

b

Метод Симпсона (парабол)

Точность приближенного возрастает, если подинтегральную функцию y = f(x) на отрезке [a,b] интерполировать участками парабол, то в этом случае используется метод Симпсона. Для увеличения точности вычислений отрезок [a,b]на n пар участков [x2n-2, x2n-1, x2n]. Вычисление определенного интеграла проводится по формуле:

В работе используете три варианта вычисления определенного интеграла, для этого используете следующие элементы управления: 3 переключателя, кнопку – вычислить, счетчик и поле для ввода n – число интервалов, поле – значение x.

ex dx Метод прямоугольников,

xb

7. Решение нелинейных уравнений

Необходимость отыскания корней нелинейных уравнений встречается при расчетах линейных систем автоматического уравнения, собственных колебаний машин и конструкций со многими степенями свободы и т. д. Основная форма записи этих уравнений F(x)=0 .

Имеются две разновидности нелинейных уравнений: алгебраические и трансцендентные.

экспоненциальные и другие функции от некоторого аргумента x, например, e-x+sinx = 0 . Такие уравнения обычно имеют бесконечное множество корней.

Поиск корней нелинейного уравнения состоит из трех этапов: определение границ существования корней, отделение корней и уточнение корней.

Определение границ существования корней

Определение границ действителных корней алгебраического уравнения F(x)=0 . Если R1 - верхняя граница положительных корней F(x) , R2 - верхняя граница положительных корней F(-

44

положительных корней xnF( 1), то все отличные от нуля действительные корни уравнения x

F(x)=0 (если они существуют) лежат внутри интервалов ( R2 , 1 ) и ( 1 ,R1) .

R4 R3

Для определения верхней границы положительных корней алгебраического уравнения можно формулой Лагранжа.

полинома Pn(x)=A0xn+A1xn-1+…+An; B – наибольшее из абсолютных значений отрицательных коэффициентов полинома F(x). Для использования формулы (1.1) необходимо, чтобы коэффициент A0 был положительным (A0>0).

Отделение корней

Все действительные корни нелинейного уравнения F(x)=0 лежат на оси абсцисс. Отделение корней производится следующим образом: перемещаясь по оси х от нижней границы существования корня Rn на величину шага поиска е и проверяя смену знак функции F(x), в текущей координате х найти такой интервал е, на котором произошла смена знака функции или функция попала на ось (F(x)=0). Этот интервал и будет определять нижнюю и верхнюю границы существования одного из корней нелинейного уравнения. Смену знака определяют по произведению значений функций в двух соседних точках: F1= F(x-e) и F2= F(x). Условие смены знака - F1* F2≤0. После определения выделенного корня происходит отделения следующего корня. Этот процесс продолжается до достижения верхней границы существования корней.

Уточнение корней

Существует множество методов уточнения корней.

Метод половинного деления. Суть этого метода заключается в делении интервала между нижней и верхней границей существования корня пополам. Новое значение корня определяется как х=(хн+хв)/2. Если F (x)=0, то х точный корень уравнения. Если же F (x)≠0 , то из двух образовавшихся отрезков [хн,х] и [х,хв] выбирается тот, на концах которого функ-ция F (x) принимает значения противоположных знаков. Затем полученный отрезок делится пополам и проводятся те же вычисления. Процесс деления отрезка пополам производится до тех пор, пока полученные при делении отрезки не станут меньше заданной точности е.

Метод итераций. Для использования этого метода нужно преобразовать исходное уравнение F(x)=0 к виду x=FI(x), где FI(x)= F(x)+x. Корни уравнения в этом случае будут находится на пересечении двух кривых Y=x и Y=FI(x). Поиск этого корня производится

исходя из полученного уравнения x=FI(x),следующим образом: x[i+1]=FI(x[i]). Процесс поиска все новых приближений x[i+1] продолжается до тех пор, пока не будет выполняться

Метод касательных. Заключается в проведении касательной в текущей точке x[i]. Пересечение касательной с осью х дает новое, более точное значение x[i+1], т.е. x[i+1] = (x[i])-

Т, где T=F(x[i])/F (x[i]) – изменение аргумента, которое находится путем деления противолежащего катета F(x[i]) на тангенс угла наклона касательной tga = F (x[i]). Этот процесс продолжается до тех пор пока изменение аргумента Т не станет меньше заданной точности е, т.е. Т≤ е. Дано алгебраическое уравнение 8x4-8x2-32x+1=0

1.Написать процедуру - определение границ действителных корней алгебраического уравнения, функцию – вычисление значения функции для нахождения границ.

2.Написать процедуру – отделение корней.

45

3.Уточнение корней методом половинного деления. Уравнение 8x4-8x2-32x+1=0.

Уточнить до ε = 0.001 корень уравнения методом половинного деления.

Уточнение корней методом итераций.Уравнение Найти корень уравнения x3-2.56x2- 1.3251x+4.395006=0. За начальное приближение к корню взято число 2, а корень вычисляется c точностью до 0.00001.

4. Уточнение корней методом касательных . Уравнение 8x4-8x2-32x+1=0

8. Решение систем линейных алгебраических уравнений

Решение системы линейных алгебраических уравнений используется при расчете электрических цепей постоянного и переменного тока и при решении многих других задач.

Система линейных алгебраических уравнений имеет вид: a11x1+a12x2+…+a1nxn=a1,n+1

a21x1+a22x2+…+a2nxn=a2,n+2

…............................................ an1x1+an2x2+…+annxn=an,n+1

По коэффициентам системы составляют расширенную матрицу

Одним из методов решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных (метод Гаусса), который состоит из двух этапов.

1 этап - исключение переменных

Переменную x1 исключают из 2, 3, … , n-го уравнения . Переменную x2 исключают из 3, … , n-го уравнения и т.д. Наконец, переменную xn-1 исключают из n-го уравнения.

Для исключения, допустим, переменной xk из i-го уравнения, необходимо сначала определить множительный коэффициент C=aik/akk , как отношение элементов k-го столбца, расположенных в i-ой и k-ой строках. Далее каждый элемент i-ой строки изменяется путем вычитания соответствующего элемента k-ой, умноженного на коэффициент С, т.е.

aij=aij-akj*C.

Врезультате таких преобразований элемент aik получит значение 0, а остальные элементы изменятся.

Впроцессе исключения переменных изменяются элементы расширенной матрицы, и она приобретает следующий вид:

В квадратных скобках указано количество преобразований элементов расширенной матрицы.

46

2 этап - нахождение корней системы

По элементам последней строки матрицы (1.2) можно найти значение

xn a[nn,n11] /ann[n 1] . Значение корня xn используется для нахождения значения xn-1 по элементам (n-

1)-ой строки и найденные корни xk+1, xk+2, … , xn будет найдено как

n

xk (ak[k,n11] akj[k 1] xj )/a[kkk 1] j k 1

В работе используйте кнопку метод Гаусса, счетчик и поле для ввода n – количества неизвестных. Матрицу коэффициентов расположите на листе Excel. Зарезервируйте два массива. В первый массив копируете матрицу, во втором выполняете исключение очередного неизвестного, а затем заменяете первую матрицу. Корни уравнения выводите на лист Excel.

Решите следующую систему уравнений: 2x1+3x2+7x3+6x4=1

3 x1+5 x2+3 x3+ x4=3 5 x1+3 x2+ x3+3 x4=4 3 x1+3 x2+ x3+6 x4=5

9. Приближенные методы решения систем алгебраических уравнений

Наиболее распространенным приближенным методом решения является метод Зейделя. Суть метода заключается в том, что каждое уравнение разрешается относительно своей k-ой переменной и это значение считается новым приближением этой переменной, т.е.

запоминается в элементах массива Tk=| x[ki 1] -x[ki] |. Процесс поиска заканчивается, если все значения Tk окажутся меньше некоторой малой величины .

В работе используйте кнопку – метод Зейделя, счетчик и поле для ввода n – количество неизвестных, поле для ввода . Матрицу коэффициентов располагаете на листе Excel. Корни

уравнения выводите на лист Excel. Начальное приближение x10 ,x20 ,x30 ,x40 , задаете в ячейках

листа.

Решите следующую систему уравнений: 2x1+3x2+7x3+6x4=1

3 x1+5 x2+3 x3+ x4=3 5 x1+3 x2+ x3+3 x4=4 3 x1+3 x2+ x3+6 x4=5

Литература Н.И. Данилина, Н.С. Дубровская и др. «Численные методы». Высшая школа 1976г.

10. Интерполяция функций, заданных таблично

Для исследования систем автоматического управления с нелинейными элементами, характеристики которых заданы в виде таблицы значений и моделирования таких

47

характеристик на ЭВМ, применяются методы интерполяции. Эти методы позволяют подобрать полином, описывающий нелинейную зависимость, представленную таблично.

Интерполяция – это подбор полинома m-ой степени, обеспечивающий прохождение функции через узловые точки. Количество узловых точек должно быть m+1.

Метод Лагранжа Полином, формируемый методом Лагранжа, имеет вид

Pm(x)=Y1B1(x)+Y2B2(x)+…+Ym+1Bm+1(x),

где Bj(x) – многочлен m-ой степени. Многочлены Bj(x) могут принимать только два значения – либо 0, либо 1.

Полином формируется сразу после ввода исходных данных для любой контрольной точки. В работе используйте кнопку – метод Лагранжа, счетчик и поле для ввода m – степень полинома, счетчик и поле для ввода Kkt – количество контрольных точек. Координаты узловых точек (X1 ,Y1)… (Xm+1 ,Ym+1) и значения контрольных точек (Xk) вводятся в колонки листа Excel. Для каждой контрольной точки вычисляется значение полинома.

Функция f(x) задана таблично:

Значения контрольных точек выбрать самостоятельно.

11. Допольнительные курсовые работы для студентов горно-геологических специальностей

1. Вычисление координат замкнутого теодолитного хода

На горизонтально ориентированном листе Excel разместить таблицу - ведомость вычислений. В нее занести исходные данные - столбцы 1,2,3,9 и данные в первой строке столбцов 6,7,14,15. В первой (широкой) строке, справа от заголовка, разместить переключатели (Option Buttons) с надписями (свойство Caption) Левые углы и Правые углы, а еще правее кнопку с надписью Вычислить. Кнопке должна соответствовать событийная процедура вычисления координат замкнутого теодолитного хода. В результате вычислений должны быть последовательно заполнены пустые ячейки таблицы. Невязки углов и приращений координат до и после уравнивания разместить в соответствующих столбцах, под таблицей, пропустив одну строку. В приведенном примере измерены левые углы.

48

Вычисление координат замкнутого теодолитного хода

Вариант 1. Отладку программы выполнить на примере, приведенном в таблице. Вариант 2. Программу отладить на примере, в котором измерены правые углы.

Исходные данные этого примера. Столбец 1: 1, 2, 3, 4, 5, 6.

Столбец 2: 122, 98, 153, 90, 203, 52. Столбец 3: 28, 8, 27, 1, 12, 46.

Столбец 9: 301.77, 284.67, 254.52, 318.33, 242.37, 524.88.

Значения для первой точки в столбцах 6,7,14,15: 163, 17, 461.83, 235.49.

2. Разработка приложения “Прямая геодезическая задача”

На листе Excel разместить таблицу, содержащую 5 столбцов с именами: N-номер пункта, A-дирекц. угол (град.), d-гориз. Пролож. до след. пункта, X, Y -координаты. Ввести данные тестового примера (для 3-7 пунктов) в столбцы N,A,d, а для первого пункта - и в столбцы X,Y. Программа должна вычислять координаты X,Y остальных пунктов.

Рекомендации.

На листе Excel разместить переключатели (Option Buttons) с надписями (свойство Caption) Левые углы и Правые углы, а еще правее кнопку с надписью Вычислить. Кнопке должна соответствовать событийная процедура вычисления координат пунктов. Программу надо отладить на примерах, когда измерены левые и правые углы.

3. Разработка приложения “Обратная геодезическая задача”

Задача аналогична предыдущей (см. работу 2), только заданными являются столбцы N, X, Y, а вычислить надо дирекционные углы и горизонтальные проложения в столбцах A, d.

49

4.Разработка приложения “Преобразование географических координат

впрямоугольные и прямоугольных в географические”

Эта курсовая работа особенно полезна для студентов, будующая специальность которых имеет отношение к наукам о Земле (геология, геодезия, экология, горное дело и т.п.). Но, вообще говоря, представлять системы координат, в которых строятся различные карты, должен каждый образованный человек. Известно, что в качестве геометрической модели Земли используют эллипсоид. В России обычно применяют параметры эллипсоида Красовского:

a = 6 378 245.000 м - большая полуось,

b = 6 356 863.019 м - малая (полярная) полуось,

e12 = 0.006 693 4216 – квадрат первого эксцентриситета,

e22 = 0.006 719 2188 – квадрат второго эксцентриситета. Для перехода к прямоугольным координатам эллипсоид (как

дыню) разрезают от полюса к полюсу на шестиградусные зоны (дольки). Каждая зона-долька как-бы распрямляется – делается плоской. Координата X отсчитывается от экватора, а Y – от осевого меридиана зоны с добавлением 500 км. Эта добавка к координате Y служит для того, чтобы координаты Y были положительными. Таким образом, в каждой зоне свои координаты Y, отсчитываемые от своего осевого меридиана.

Каждая шестиградусная зона делится еще параллелями через 4 градуса, и получаются листы, для которых строятся карты масштаба 1:1000000 (в 1 см 10 км).

Каждый лист миллионного масштаба делится на 36 листов масштаба 1:200000 или на 144 листа масштаба 1:100000 (в 1 см 1 км) – так строятся карты в прямоугольных координатах.

Обозначим широту точки через LT (Latitude – широта), а долготу – через LN (Longitude – долгота). С формулами для расчета X, Y по известным значениям LT, LN при заданном осевом (центральном) меридиане CM можно познакомиться по указанным в конце этой работы книгам. Вместо формул, здесь просто приведем начало модуля, содержащего общую процедуру LTLNtoXY, пересчитывающую географические координаты в прямоугольные, и опишем постановку остальных задач, которые надо запрограммировать, чтобы завершить разработку приложения.

Option Explicit

Const Pi180 As Double = 0.0174532925 Const A As Double = 6378245

Const B As Double = 6356863.019

Const EE1 As Double = 0.0066934216

Const EE2 As Double = 0.0067192188

Private Sub LTLNtoXY(LT As Double, LN As Double, X As Double, Y As Double, CM As Double)

'LT – ШИPOTA (радианы)

'LN – ДOЛГOTA (радианы)

'CM - ОСЕВОЙ MEPИДИAH (градусы)

'X, Y – KOOPДИHATЫ (км)

Dim N As Double, DL As Double, S As Double, DL2 As Double, T As Double, T2 As Double Dim SINLT As Double, COSLT As Double, COS2 As Double, COS3 As Double, COS5 As Double Dim A2 As Double, A4 As Double, B1 As Double, B3 As Double, B5 As Double, T4 As Double

DL = LN - CM * Pi180: DL2 = DL * DL

SINLT = Sin(LT): COSLT = Cos(LT): T = SINLT / COSLT T2 = T * T: T4 = T2 * T2

COS2 = COSLT * COSLT: COS3 = COSLT * COSLT * COSLT: COS5 = COS2 * COS3 N = A / Sqr(1 - EE1 * SINLT * SINLT)

S = 6367558.49587 * LT - 16036.48027 * Sin(2 * LT) + _ 16.828067 * Sin(4 * LT) - 0.021975 * Sin(6 * LT)

A2 = N * SINLT * COSLT / 2: A4 = N * SINLT * COS3 * (5 - T2) / 24

50