Порядок выполнения работы

1. Измерить штангенциркулем диаметр шарика d.

2. Установить максимальную длину нити. Линейкой измерить расстояние L от точки подвеса до нижнего края шарика.

3. Отклонить маятник на угол 15-20⁰от вертикали. Измерить секундомером времяt10 полных колебаний (n= 10). Измерения повторить 3 раза.

4. Результаты измерений и погрешности измерительных приборов занести в таблицу.

5. Произвести математическую обработку результатов измерений, найти по формуле (1) ускорение свободного падения gи его погрешность g. При расчете погрешности удобно применять метод логарифмирования функции.

6. Сравнить полученное значение ускорения с соответствующим значением gдля данной географической широты.

Таблица измерений

d, мм	d, мм	L, см	L, см	n	t, c	t, с

Контрольные вопросы

1. Дайте понятие о неинерциальных системах отсчета.

2. Что понимается под силой тяготения, силой тяжести и весом тела?

3. Какое ускорение называется ускорением свободного падения?

4. От каких величин зависит ускорение свободного падения?

5. Объясните зависимость ускорения свободного падения тел от географической широты местности.

6. Что такое математический маятник? Запишите формулу периода математического маятника.

7. Выведите расчетную формулу.

Лабораторная работа 5-3 Определение ускорения свободного падения с помощью физического маятника

Цель работы: вычислить ускорение свободного падения тел, измеряя период колебаний физического маятника, определить параметры физического маятника.

Приборы и принадлежности: физический маятник, математический маятник, секундомер, масштабная линейка.

Методика и техника эксперимента

Физическим маятникомназывается твёрдое тело, способное совершать колебания вокруг неподвижной осиО, не проходящей через центр инерцииС. На него действуют сила тяжестиmgи сила реакции со стороны оси .

Поскольку все точки маятника движутся по окружностям, центры которых расположены на одной оси, его движения является вращательным. При отклонении маятника от положения равновесия на угол возникает вращательный моментMсилы тяжести

,

где m– масса маятника,d- расстояние от оси вращения до центра масс системы. Знак “минус” обусловлен противоположной направленностьюиM. Момент силы реакции оси равен нулю, т.к. линия действия силы проходит через ось вращения.

Применим основной закон динамики вращательного движения:

,

в котором - угловое ускорение,J- момент инерции маятника. Преобразуя его к виду

и учитывая, что при малых углах отклонения маятника , получим дифференциальное уравнение колебательного процесса:

.

Как нетрудно увидеть путем прямой подстановки, решение данного уравнения имеет вид:

,

т.е. угол  изменяется по гармоническому закону, тело совершает гармонические колебания с циклической частотой и периодом

. (1)

Приведенная длинафизического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Формула для периода колебаний математического маятника имеет вид:

. (2)

Из сравнения выражений (1) и (2) видно, что приведенная длина физического маятника равна:

. (3)

Отложим от точки подвеса Овдоль прямойОСотрезокОО, длина которого равна приведенной длине физического маятникаl. ТочкаОназываетсяцентром качания. Центр качания можно определить как точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.

П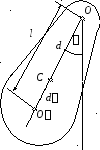о теореме Штейнера

.

Подставив это выражение в формулу (3), получим следующее выражение для приведенной длины:

. (4)

Отсюда следует, что, во-первых, l>d, т.е. точка подвесаОи центр качанияОлежат по разные стороны от массСи, во-вторых, что всем точкам

подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина, а, следовательно, один и тот же период колебаний Т.

Точка подвеса и центр качания являются взаимнымиилисопряженнымиточками в следующем смысле. Если маятник подвесить за центр качанияО, то его период не изменится и прежняя точка подвесаОсделается новым центром качания. Это положение называется теоремой Гюйгенса.

Пусть Оявляется точкой подвеса. Тогда приведенная длина в соответствии с (4) будет

.

Из рисунка видно, что , а в соответствии с (3). Подставив это значение в предыдущую формулу, получим:

,

т.е. приведенная длина, а следовательно, период колебаний физического маятника остались без изменений.

Теорема Гюйгенса используется в оборотном маятникедля измерений ускорения свободного падения. Физический оборотный маятник, используемый в данной работе, состоит из металлического стержня, на котором жестко закреплены две опорные призмыОи О, и три чечевицы. Две из них находятся на концах стержня, их положение не изменяется при проведении эксперимента. Третья подвижная чечевицаАнаходится между опорными призмами. Путем перемещения чечевицыАможно менять расстояниеdмежду точкой подвесаОи центром тяжестиС, а также расстояниеdмежду центром тяжестиСи центром качанияО.

Перемещением этой чечевицы достигают совпадения периодов колебаний маятника, когда точками подвеса являются ребра опорных призмОи О. Поэтому при совпадении периодов колебаний расстояние между ними дает приведенную длину физического маятникаl. Измеряя период колебанийТ, можно вычислить ускорениеgпо формуле, полученной из (2):

.

Используя формулу для периода колебаний , окончательно находим:

. (5)

Из (3) можно выразить момент инерции маятника относительно оси подвеса О:. Собственный момент инерции маятника относительно оси, проходящей через его центр массJ₀, связан сJпо теореме Штейнера:

,

откуда

или

. (6)