Met_MatStat385_08

ГОУВПО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

385 - 2008

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы

по курсу "Высшая математика" для студентов специальностей 280103 "Защитавчрезвычайныхситуациях",

280101 "Безопасностьжизнедеятельностивтехносфере" и

280200 "Защитаокружающейсреды" очной формы обучения

Воронеж 2008

Составители: канд. физ.-мат. наук И.Н. Пантелеев аспирант А.И. Пантелеев

УДК 51 (075)

Элементы математической статистики: методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов специальностей 280103 "Защита в чрезвычайных ситуациях", 280101 "Безопасность жизнедеятельности в техносфере" и 280200 "Защита окружающей среды" очной формы обучения. / ГОУВПО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев, А.И. Пантелеев. Воронеж, 2008. 37 с.

Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" по разделу «Математическая статистика» для студентов специальности

280103 (ЧС), 280101 (БЖ) и 280200 (ЗС) в 4 семестре. В работе приведен теоретический материал, необходимый для выполнения заданий и решение типовых примеров.

Табл. 3. Ил. 2. Библиогр.: 8 назв.

Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

© ГОУВПО «Воронежский государственный технический университет», 2008

1.Основные понятия математической статистики

1.1.Генеральная совокупность. Выборка. Основные типы задач математической статистики

Пусть Х – некоторая случайная величина (количественный признак). В дальнейшем все значения этой СВ будем называть генеральной совокупностью. Если, например, Х – дискретная СВ, то генеральная совокупность – х1 , х2 , …, хn.

Допустим, что в процессе наблюдений или опытов мы получили n значений (х1 , х2 , …, хn) случайной величины Х. В дальнейшем будем говорить, что сделали выборку х1 , х2 , …, хn из генеральной совокупности Х.

Число n называется объемом выборки.

Выборку х1 , х2 , …, хn из генеральной совокупности Х также можно представить, как значения n экземпляров х1 , х2 , …, хn случайной величины Х.

Заметим, что среди элементов выборки могут быть повторяющиеся. Поэтому для каждого элемента хi выборки говорят о частоте ее появления, т.е. сколько раз число хi наблюдалось в выборке.

В дальнейшем мы часто будем задавать выборку в виде

где х1 , х2 , …, хm – различные элементы выборки, а n1, n2, …, nm – частоты элементов выборки.

Ясно, что в этом случае объем выборки n = n1 + n2 +…+ nm . Значения х1 , … , хm выборки будем называть вариантами. Если варианты выборки расположены в возрастающем

порядке, то выборка называется вариационным рядом.

Например,

Варианты выборки называются равноотстоящими, если

Хi+1 − Xi = h, где h – постоянное число.

На практике при описании реальных процессов различные характеристики процесса являются случайными величинами. Поэтому возникают задачи определения законов распределения, математических ожиданий и других характеристик этих СВ, основываясь на изучении выборок.

Пусть значения СВ Х определяют генеральную совокупность и F(x)=P(X < x) – интегральная функция распределения Х. В дальнейшем мы будем ее называть теоретической функцией распределения генеральной совокупности Х. Зная функцию F(x), можно определить все характеристики СВ Х. Поэтому поставим перед собой следующую задачу: можно ли с помощью выборок из генеральной совокупности Х приближенно найти функцию F (x) ?

Пусть задана выборка объема n = n1 + n2 + … + nm.

функцией распределения выборки или эмпирической функцией распределения.

2

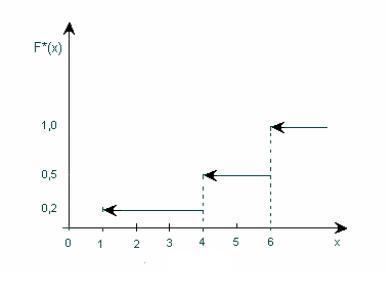
Пример 1. Найти эмпирическую функцию по выборке

Решение. Найдем объем выборки n = 10 + 15 + 25 = 50. Наименьшаявариантаравнаединице, следовательно, F *(x) = 0

при х ≤ 1. Значение Х < 4, а именно х1 = 1, наблюдалось 10 раз, следовательно,

F *(x) = 1050 = 0,2 при 1 < Х ≤ 4.

Значения Х < 6, а именно х1 = 1 и х2 = 4, наблюдались n1 + n2 = 10 + 15 = 25 раз, следовательно,

Графически эта функция изображена на рис.1.

3

Рис.1

Эмпирическая функция F *(x) является приближением теоретической функции F(x) , и чем больше объем выборки n, тем точнее F *(x) описывает F(x) (по вероятности, т.е. случайные отклонения маловероятны).

1.2. Статистическая оценка параметров распределения

Пусть значения случайной величины Х образуют генеральную совокупность. Закон распределения СВ (например, нормальный закон) Х нам известен. Однако неизвестны некоторые параметры этого распределения (например, МО или дисперсия).

Требуется, изучая выборки из генеральной совокупности, оценить, т.е. приближенно найти, неизвестный параметр.

Статистической оценкой неизвестного параметра называется всякая функция ϕ варианта хi выборки, дающая

приближенное значение этого параметра. 4

Если обозначим неизвестный параметр через θ , а его оценку через θ *, то θ* =θ (х1,…хn), где x1, … , xn – выборка из генеральной совокупности Х.

Рассматривая варианты x1, … , xn выборки как значения n экземпляров Х1, …, Хn СВ Х, получим:θ* =ϕ (Х1, …, Хn), т.е. статистическая оценка θ * является функцией от случайных величин Х1, …, Хn,, а значит и сама является СВ. Таким образом статистическая оценка θ * принимает значения (различные) в зависимости от выборки.

Ясно, что для одного и того же неизвестного параметра можно построить различные статистические оценки. Наша задача понять, какие оценки являются «хорошими».

Во-первых, естественно желание, чтобы статистическая оценка, являясь случайной величиной, имела своим математическим ожиданием неизвестный параметр.

Статистическая оценка θ * неизвестного параметра θ называется несмещенной, если Μ(θ*) =θ .

Во-вторых, естественно требовать, чтобы значения статистической оценки θ * неизвестного параметра θ , которая называется эффективной, если она обладает наименьшей дисперсией среди всех статистических оценок параметра θ .

В-третьих, естественно считать, что, чем больше объем выборки, тем точнее значение статистической оценки определяет неизвестный параметр.

Статистическая оценка θ * неизвестного параметра θ называется состоятельной, если она стремится по вероятности к θ , т.е.

1.3. Генеральная средняя. Выборочная средняя

Пусть значения случайной величины Х образуют генеральную совокупность. Математическое ожидание Х

будем называть генеральной средней и обозначать xΓ , т.е.

xГ = M (X ) .

Рассмотрим некоторую выборку х1 , х2 , …, хn (варианты могут повторяться) из генеральной совокупности Х. Будем ее рассматривать как значения n экземпляров Х1, Х2 …, Хn СВ Х.

которая называется выборочной средней. Конкретное значение

статистической оценки XB при выборке х1 , х2 , …, хn будет:

несмещенной и состоятельной статистической оценкой для

1.4. Выборочная дисперсия

Пусть значения СВ Х образуют генеральную совокупность. Дисперсию D(X) CB X будем называть генеральной дисперсией и обозначать DΓ , а среднее квадратическое

отклонение σ Γ = DΓ .

Требуется найти статистическую оценку для DΓ .

Пусть х1, х2, …, хn – выборка из генеральной совокупности Х, а Х1, Х2 …, Хn – n экземпляров Х. Рассмотрим статистическую оценку

которая называется выборочной дисперсией. DB -случайная величина. Ее конкретное значение при данной выборке х1 , …, хn

дисперсией).

Если выборка из генеральной совокупности задана в виде таблицы

Пример 2. Пусть выборка задана таблицей

DB является смещенной статистической оценкой для D(X).

Поэтому рассматривают статистическую оценку s2 = nn−1 DB ,

которая называется исправленной выборочной дисперсией. s2 является несмещенной статистической оценкой для DΓ .

Нетрудно видеть, что при больших n : s2 ≈ DB .

исправленным выборочным среднеквадратическим отклонением.

Пример 3. Пусть генеральная совокупность X подчинена нормальному закону. Требуется оценить ее параметры.

Так как параметрами нормального распределения являются σ =σΓ и a = M (X ) = xΓ , то

σ≈σ при объеме выборки n ≤ 30 ,

σ≈σB при объеме выборки n > 30 .

8

1.5. Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормального распределения при известном σ

Пусть СВ Х образует генеральную совокупность и θ - неизвестный параметр СВ Х . Если статистическая оценка θ * является состоятельной, то чем больше объем выборки, тем точнее получаем значение θ . Однако на практике мы имеем выборки не очень большого объема, поэтому не можем гарантировать большую точность.

Пусть θ * - статистическая оценка для θ . Величина θ *−θ

называется точностью оценки. Ясно, что точность это СВ, т.к. θ * - случайная величина. Зададим малое положительное число

δ и потребуем, чтобы точность оценки θ *−θ была меньше

δ , т.е. θ *−θ <δ .

Мы не можем категорически утверждать, что оценка θ * удовлетворяет неравенству θ *−θ <δ ; можно лишь говорить о вероятности γ , с которой это неравенство выполняется.

Надежностью γ или доверительной вероятностью оценки θ по θ * называется вероятность γ , с которой осуществляется

γ = P{θ *−δ <θ <θ *+δ}.

9

Интервал (θ *−δ,θ *+δ ) называется доверительным

интервалом, т.е. доверительный интервал покрывает неизвестный параметр θ с вероятностью γ . Заметит, что

концы доверительного интервала являются случайными и изменяются от выборки к выборке, поэтому точнее говорить,

что интервал (θ *−δ,θ *+δ ) покрывает неизвестный параметр

θ , а не θ принадлежит этому интервалу.

Пусть генеральная совокупность задана случайной величиной Х, распределенной по нормальному закону, причем,

Требуется найти доверительный интервал для а при заданной надежности γ .

Выборочная средняя

X B = X1 +…+ Xn n

является статистической оценкой для xΓ = a .

Теорема. Случайная величина xB имеет нормальное распределение, если Х имеет нормальное распределение, и

где Φ(z) - функция Лапласа. Тогда имеем:

Обозначив δσn = t , получим Φ(t) =γ . Так как γ задана,

то по таблице значений функций Лапласа находим значение t .

Если задана выборка из генеральной совокупности Х

xB −t σn < a < xB +t σn .

Пример 4. Найти доверительный интервал для оценки математического ожидания а нормального распределения с

надежностью 0,95, зная выборочную среднюю XB =10,34 ,

объем выборки n =100 и среднее квадратическое отклонение

σ = 5.

11

Найдем t из соотношения 2Φ(t) = 0,95 , получим: Φ(t) = 0,475 . По таблице находим t =1,96 . Найдем точность оценки

σB = dB = 19,96 = 4,47 .

Смысл полученного результата таков: если будет произведено большое число выборок, то 95% из них определяет доверительные интервалы, в которых математическое ожидание будет заключено.

2. Методы расчета характеристик выборки

Рассмотрим рациональные методы определения

характеристик выборки xB и dB .

2.1. Условные варианты. Метод произведений

Пусть выборка из генеральной совокупности Х является вариационным рядом с равноотстоящими вариантами, т.е.

Условными называют варианты ui , определяемые равенством

12

u i = xih− c ,

где С – ложный нуль. Обычно полагают С равным варианте с наибольшей частотой.

Нетрудно видеть, что условные варианты принимают только целые значения, и, если xi 0 = C , то uio = 0 .

Условные варианты u1 , u2 , ...,un образуют условную выборку

Тогда можно определить условные эмпирические моменты порядка k :

m

∑ni ui k

Определив условные выборочные моменты первого и второго порядка

можно определить выборочные среднюю и дисперсию:

xB = M 1* h +C ,

dB = M 2 *−(M 1*)2 h2 .

13

Найти методом произведений выборочные среднюю, дисперсию и среднее квадратическое отклонение.

Решение. Составим расчетную таблицу, для чего:

1)запишем варианты xi в первый столбец;

2)запишем частоты ni во второй столбец;

3)В качестве ложного нуля С выберем варианту 20 (эта варианта имеет наибольшую частоту); в клетке третьего столбца, которая принадлежит строке, содержащей варианту 20, пишем 0; над нулем последовательно записываем условные варианты -1,-2, а под нулем – последовательно 1,2;

4) Произведения частот на условные варианты ui записываем в четвертый столбец; находим сумму этих произведений и помещаем ее в нижнюю клетку столбца;

5)Произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (80) помещаем в нижнюю клетку столбца;

6)Произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой (контрольный) столбец; сумму чисел столбца (188) помещаем в нижнюю клетку столбца.

В итоге получим следующую расчетную таблицу: 14

Контроль

∑ni ni2 +2∑ni ui +n =80 +2 4 +100 =188 ;

∑ni (ui +1)2 =188

Совпадение найденных сумм свидетельствует о том, что вычисления произведены правильно.

Вычислим условные моменты первого и второго порядков:

2.2. Эмпирические и теоретические частоты

Пусть значения СВ Х образуют генеральную совокупность. Закон распределения Х неизвестен.

Рассмотрим некоторую выборку объема n из генеральной совокупности

эмпирическими частотами.

Пусть Х – дискретная СВ и имеются основания предположить, что изучаемая величина Х распределена по некоторому определенному закону. Зная закон распределения Х, мы можем найти вероятности pi появления значений xi ,

т.е.

pi = P{X = xi} .

Теоретическими частотами ni называют частоты, определяемые по формуле ni = n pi .

Нетрудно видеть, что ni указывает, сколько раз должно появиться в среднем значение xi случайной величины Х с

предполагаемым законом распределения.

Пусть теперь Х – непрерывная СВ. Рассмотрим более детально определение теоретических частот, предполагая, что

Х- нормально распределенная случайная величина. Пусть

n = n1 +...+nm , равноотстоящая выборка из генеральной совокупности Х, n1 ,..., nm - эмпирические частоты, xi +1 − xi = h .

Тогда теоретические частоты определяются по формуле n′i = n pi ,

Значения функции (ϕ) находится по таблице.

3. Статистическая проверка гипотез

Во многих случаях результаты наблюдений используются для проверки предположений (гипотез) относительно либо самого вида распределения генеральной совокупности, либо значения параметров уже известного распределения – статистических гипотез. Пусть известно распределение СВ X (например, это нормальный закон), и по выборке необходимо проверить гипотезу о значении некоторого

параметра ( x Γ , DΓ или σΓ ) этого распределения.

В дальнейшем выдвигаемую и проверяемую гипотезу будем называть нулевой гипотезой (или основной) и

или нет. При проверке гипотезы H 0 по результатам выборки могут быть допущены ошибки двух родов: 1)ошибка первого рода – отвергнутая правильная гипотеза; 2)ошибка второго рода – принятая неправильная гипотеза. Последствия этих ошибок неравнозначны, и роль каждой оценивается до конца по условиям конкретной задачи. Например, если при проверке качества партии деталей по выборке из нее в качестве H 0 принята гипотеза, что доля брака не более 0,1% , то при допущении здесь ошибки первого рода будет забракована годная продукция, а допустив ошибку второго рода, выпустим потребителю партию деталей с долей брака больше допустимого. Перед началом анализа выборки фиксируют очень малое число α . Вероятность совершить ошибку первого рода называется уровнем значимости α . Обычно берут

α =0,05; 0,01; 0,005.

Правило, по которому принимается решение принять или отклонить гипотезу H 0 , называется критерием или статистическим критерием К. Выбор К зависит от конкретной задачи.

Обычно критерий проверки гипотезы реализуется с помощью некоторой статистической характеристики, определенной по выборке, т.е. с помощью некоторой статистики θ . Здесь θ - некоторая СВ, закон распределения которой известен.

В множестве всех возможных значений статистики q критерия К выделим подмножество ω0 , при котором гипотеза

H 0 отклоняется. Это подмножество называется критической областью. То множество значений θ , при котором гипотезу H 0 не отклоняют, называется областью принятия гипотезы (допустимой областью). Точки, разделяющие эти области, 18