Met_MatStat385_08

называются критическими точками. Для определения критических точек используют принцип практической невозможности событий, имеющих малую вероятность. При этом задаются достаточно малой величиной α , называемой уровнем значимости критерия, и определяют критическую область как множество тех значений θ , вероятность которых принадлежать к области ω0 равнялась бы α , т.е.

P{θ ω0 } =α .

Если по данным выборки при данном уровне значимости получается, что θ ω0 , то это может служить основанием для

отклонения гипотезы H 0 .

Рассмотрим проверку гипотезы о нормальном распределении генеральной совокупности X . Пусть распределение X неизвестно, но есть основание предположить, что X имеет нормальное распределение, т.е. выдвигается гипотеза H 0 о нормальности СВ X . Статистический критерий, с помощью которого проверяется нулевая гипотеза, называется критерием согласия. Имеется несколько критериев согласия. Обычно в них используются статистики, имеющие таблицы распределений, подготовленные заранее: статистику с нормальным

нормированным распределением, статистику χ2 и статистику Фишера. Рассмотрим критерий согласия Пирсона (критерий

называемые теоретическими частотами, в противоположность чему ni здесь называют эмпирическими частотами.

В качестве статистики θ выбирают СВ χ2 :

χ2 = ∑s (ni −n′i )2 . i=1 n′i

Она подчиняется распределению χ2 с числом степеней

свободы v = s −r −1 , где s - число различных значений xi ; r - число параметров, от которых зависит распределение. Для

нормального закона таких параметров два: a = xB = M (X ) и

σ = s = DB nn−1 , т.е. r = 2 , и v = s −3 . Если эмпирическое и

теоретическое распределение совпадают, то χ2 = 0 . По данному уровню значимости а и числу степеней свободы v в

принимают. В этом случае опытные данные выборки хорошо согласуются с гипотезой о нормальном распределении генеральной совокупности.

Пример 6. При уровне α = 0,05 проверить гипотезу о

нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

степеней свободы распределения χ2 равно 7-3=4. По таблице критических точек распределения χ2 , по уровню значимости α = 0,05 и числу степеней свободы 4 находим χ2крит. =9,5. Вычислим χ2набл. , для чего составим расчетную таблицу.

Решение.

1.Найдем методом произведений выборочные: среднюю, дисперсию и среднее квадратичное отклонение. Воспользуемся методом произведений, для чего составим таблицу 1.

В качестве ложного нуля принимаем С=5,8 – варианта с

столбцы.

Последний столбец служит для контроля вычислений по тождеству:

∑ni (ui +1)2 = ∑niui2 +2∑niui +n

x= h1 u +C1 ; y = h2 v +C2 ; σx = h1σu ; σy = h2 σv Контроль: 339 =189 +2 25 +100 .

Вычисления произведены верно. Найдем условные моменты.

Вычисляем выборочную среднюю:

xB = M 1* h +C = 0,25 1,4 +5,8 = 6,15.

Находим выборочную дисперсию:

dB = M 2 *−(M1*)2 h2 = 1,89 −(0,25)2 1,42 = 3,58.

Определяем выборочное среднее квадратическое отклонение:

σB = dB = 3,58 =1,89. 2.Строим нормальную кривую.

Для облегчения вычислений все расчеты сводим в таблице 2.

23

Заполняем первые три столбца.

В четвертом столбце записываем условные варианты по формуле, указанной в «шапке» таблицы. В пятом столбце находим значения функции

Функция ϕ(ui ) четная, т.е. ϕ(−ui) =ϕ(ui) .

Значения функции ϕ(ui ) в зависимости от аргумента ui (берутся положительные ui , т.к. функция ϕ(ui ) четная)

находим из таблицы.

Теоретические частоты теоретической кривой находим по формуле

= 1001,891,4 ϕ(ui) = 74,07ϕ(ui)

И заполняем последний столбец. Отметим, что в последнем столбце частоты n′i округляются до целого числа и

∑n′i = ∑ni =100 .

Всистеме координат (xi ; yi = n′i) строим нормальную

(теоретическую) кривую (рис.2) по выравнивающим частотам n′i (они отмечены кружками). Полигон наблюдаемых частот построен в системе координат (x 'i ; yi = n i ) .

Рис. 2

3. Проверяем гипотезу о нормальности X при уровне значимости α = 0,05 .

Вычислим χ2набл., для чего составим расчетную таблицу 3.

25

Суммируя числа пятого столбца, получаем χ2набл. = 2,78 . Суммируя числа последнего столбца, получаем 102,78. Контроль: χ2набл. = 2,78

∑ni2 −∑ni =102,78 −100 = 2,78 . n′i

Совпадение результатов подтверждает правильность вычислений.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариантов) 7. v =7-3=4.

По таблице критических точек распределения χ2 , по уровню значимости α = 0,05 и числу степеней свободы v =4 находим χ2кр =9,5.

Так как χ2набл. < χ2кр. , то нет оснований отвергать нулевую

гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальности распределения генеральной совокупности.

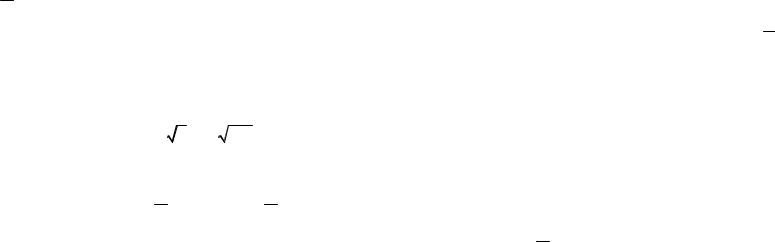
4. Найдем доверительный интервал для оценки неизвестного MO M(X), полагая что X имеет нормальное распределение, среднее квадратическое отклонение σ =σX =σB =1,89 и доверительная вероятность γ = 0,95 .

Известен объем выборки: n =100 , выборочная средняя xB = 6,15 .

Из соотношения 2Φ(t) =γ получим Φ(t) = 0,475 . По таблице находим параметр t =1,96 .

Найдем точность оценки

Доверительный интервал таков:

xB −δ < M (X ) < xB +δ

или 6,15 −0,37 < M (X ) < 6,15 +0,37 5,78 < M (X ) < 6,52 .

Надежность γ = 0,95 указывает, что если произведено

достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен.

4. Элементы теории корреляции

Корреляционный анализ – широко известный и эффективный метод статистики, позволяющий по совокупности значений показателей выявлять и описывать связи между показателями.

Если каждому значению величины X соответствует несколько значений величины Y , но число этих значений, как и сами значения, остается не вполне определенным, то такие связи называются статистическими. Например, уровень

27

производительности труда на предприятиях тем выше, чем больше его электровооруженность. Вместе с тем, нет никаких оснований утверждать об однозначности этой зависимости.

Если изменение одной из переменных сопровождается изменениями условного среднего значения другой переменной величины, то такая зависимость является корреляционной.

Под условным средним yx подразумевают среднее

yx = f (x) . Это уравнение называют уравнением регрессии Y на X , а ее график – линией регрессии Y на X .

Корреляционный анализ рассматривает две основные задачи.

Первая задача теории корреляции – установить форму корреляционной связи, т.е. вид функции регрессии (линейная, квадратичная и т.д.)

Вторая задача теории корреляции – оценить тесноту (силу)

условного среднего. Большое рассеивание свидетельствует о слабой зависимости Y от X , малое рассеивание указывает на наличие сильной зависимости.

28

4.1. Отыскание параметров выборочного уравнения прямой линии регрессии по несгруппированным данным

Пусть количественные признаки X и Y связаны линейной корреляционной таблицей и в результате независимых испытаний получены n пар чисел:

Выборочное уравнение прямой линии регрессии Y на X выбираем в виде:

y = p y x x + B .

Параметры p y x и В, которые определяются методом наименьших квадратов, имеют вид:

коэффициентом корреляции. Она служит для оценки тесноты линейной корреляционной зависимости.

Абсолютная величина выборочного коэффициента корреляции не превосходит единицы, т.е. −1 ≤ rB ≤1.

4.2. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным

При большом числе испытаний одно и то же значение X может встретиться nx раз, одно и то ж значение Y может

встретиться ny раз, одна и та же пара чисел (x; y) может встретиться nx y раз, причем обычно ∑nx = ∑ny = ∑nxy = n -

объем выборки. Поэтому данные наблюдений группируют, т.е. подсчитывают nx , ny , nx y . Все сгруппированные данные

записывают в виде таблицы, которую называют корреляционной.

Если обе линии регрессии Y на X и X наY - прямые, то корреляция является линейной.

Выборочное уравнение прямой линии регрессии Y на X имеет вид:

yx − yB = rB σ y (x − xB ),

σx

где yx - условная средняя; xB и yB - выборочные средние признаков X и Y ; σx и σ y - выборочные средние квадратичные отклонения; rB - выборочный коэффициент корреляции.

Выборочное уравнение прямой линии регрессии X на Y имеет вид:

xy − xB = rB σ y (y − yB ).

σx

Считаем, что данные наблюдений над признаками X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами.

30

Тогда переходим к условным вариантам:

где C1 - варианта признака X , имеющая наибольшую частоту; C2 - варианта признака Y , имеющая наибольшую частоту, h1 - шаг (разность между двумя соседними вариантами X ); h2 - шаг (разность между двумя соседними вариантами Y ).

Тогда выборочный коэффициент корреляции

31

Вопросы для самопроверки

1.Что такое генеральная совокупность? Что такое выборка из генеральной совокупности? Какие требования к ней предъявляются? Что такое объем выборки? размах выборки?

2.Что собой представляет статистический ряд распределения случайной величины?

3.Что такое эмпирическая функция распределения? Каково ее значение для статистики?

4.Что представляет собой гистограмма? полигон частот? Статистическими аналогами какой функции они являются?

5.Что такое выборочное среднее? Что является оценкой математического ожидания генеральной совокупности?

6.Что такое выборочная дисперсия? Оценкой какого параметра она является? Какие соотношения и в каких случаях можно использовать для оценки дисперсии?

7.Какими свойствами должны обладать оценки генеральной совокупности? Что такое несмещенность оценки? состоятельность? эффективность?

8.Что такое доверительный интервал? Как определяются доверительные интервалы изменения математического ожидания? дисперсии?

9.Что такое статистическая гипотеза? параметрическая гипотеза? гипотеза о виде распределения?

10.Что такое основная (H 0 ) и альтернативная (H 1) гипотезы?

11.Какую гипотезу проверяют статистические критерии?

12.В чем смысл ошибок первого и второго рода при проверке статистических гипотез?

13.Что такое критическая область критерия? критическая

точка?

14.Что такое критерий согласия Пирсона? Как определить

выборочную статистику χ2 («хи-квадрат»)?

15. Как определяется число степеней свободы в критерии Пирсона? Как определяется уровень значимости критерия согласия?

Задание для типового расчета по математической статистике

Выбрать таблицу по порядковому номеру студента в списке группы и составить на основе приведенной таблицы новую таблицу, элементы которой определить из соотношения:

xij = (1+k)x0ij +k , где k = N / n (N — последняя цифра номера учебной группы студента, n — две последние цифры номера студенческого билета). Параметр k округлить до 0,1.

Полученную таблицу считать таблицей исходных статистических данных для случайной величины X и использовать значения X в нижеследующих пунктах.

Пусть признак X представлен точечным (дискретным) выборочным распределением в виде таблицы выборочных значений. Требуется:

1.Составить интервальное распределение выборки.

2.Построить гистограмму относительных частот.

3.Перейти от составленного интервального к точечному выборочному распределению, взяв при этом за значения признака середины частичных интервалов.

4.Построить полигон относительных частот.

5.Найти эмпирическую функцию распределения и построить ее график.

6.Вычислить все точечные статистические оценки

числовых характеристик признака: выборочное среднее xв ; выборочную дисперсию σn2 и исправленную выборочную

дисперсию s2 ; выборочное среднее квадратическое отклонение σn и исправленное выборочное среднее

квадратическое отклонение s.

7. Считая первый столбец таблицы выборкой значений нормально распределенного признака X, построить доверительные интервалы, покрывающие неизвестные математическое ожидание и дисперсию этого признака с

надежностью γ = 0.95 .

33

8. Считая первые два столбца таблицы выборками значений нормально распределенных признаков Х1 и Х2, проверить при уровне значимости α = 0.05 гипотезу H0:

D(X1) = D(X2).

9.Проверить при уровне значимости α = 0.05 с помощью критерия Пирсона гипотезу о нормальном распределении признака X.

10.Считая первый столбец таблицы выборкой значений признака X, а второй - выборкой значений признака Y, оценить тесноту линейной корреляционной связи между признаками и составить выборочное уравнение прямой

регрессии Y на X.

Варианты № 1, 9, 17, 25

Варианты № 2, 10, 18, 26

34

Варианты № 3, 11, 19, 27

Варианты № 4, 12, 20, 28

Варианты № 5, 13, 21, 29

35

Варианты № 6, 14, 22, 30

Варианты № 7, 15, 23, 31

Варианты № 8, 16, 24, 32

36

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. - М.: Высш. шк, 1997.

2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. -

М.: Высш. шк, 2006.

3.Вентцель Е.С. Теория вероятностей / Е.С. Вентцель. -

М.: Наука, 1999.

4.Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики (типовые расчеты) / В.Ф. Чудесенко. - М.: Высш. шк, 2007.

5.Кремер Н.Ш. Теория вероятностей и математическая статистика / Н.Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2004.

6.Кибзун А.И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами / А.И. Кибзун, Е.Р. Горяинова, А.В. Наумов. – М.: Физматлит, 2002.

7.Андронов А.М. Теория вероятностей и математическая статистика / А.М. Андронов, Е.А. Копытов, Л.Я. Гринглаз. – СПб.: Питер, 2004.

8.Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике / Д.Т. Письменный.

–М.: Айрис-пресс, 2004.

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы

по курсу "Высшая математика" для студентов специальностей 280103 "Защитавчрезвычайныхситуациях",

280101 "Безопасностьжизнедеятельностивтехносфере" и

280200 "Защитаокружающейсреды" очной формы обучения.

Составители: Пантелеев Игорь Николаевич Пантелеев Андрей Игоревич

В авторской редакции

Компьютерный набор И.Н. Пантелеева

Подписано в печать 28.11.2008.

Формат 60x84/16. Бумага для множительных аппаратов. Усл. печ. л 2,4. Уч.-изд.л. 2,2. Тираж 100 экз. "С"

Заказ №

ГОУВПО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14