
matem_342-2008
.pdf
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ К ИЗУЧЕНИЮ КУРСА «МАТЕМАТИКА»
ГОУВПО «Воронежский государственный технический университет»
Кафедра «Прикладная математика»
342 -2008
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к контрольной работе № 3 по математике
для студентов специальностей 150202 «Оборудование и технология сварочного
производства» 210201 «Проектирование и технология
радиоэлектронных средств» 110302 «Электрификация и автоматизация
сельского хозяйства» заочной формы обучения с сокращенной программой
divFdV FndS
V S
Воронеж 2008
Составители: канд. физ.- мат. наук канд. физ.- мат. наук канд. физ.- мат. наук канд. техн. наук
В.Н. Дурова, М.И. Зайцева, В.И. Кузнецова, О.А. Соколова
УДК 517.2. (07)
Методические указания к контрольным работам № 3 по математике для студентов специальностей 150202 «Оборудование и технология сварочного производства», 210201 «Проектирование и технология радиоэлектронных средств», 110302 «Электрификация и автоматизация сельского хозяйства» заочной формы обучения с сокращенной программой / ГОУВПО «Воронежский государственный технический университет»; сост. В.Н. Дурова, М.И. Зайцева, В.И.Кузнецова, О.А. Соколова. Воронеж, 2008. 36 с.
Методические указания предназначены для студентовзаочников инженерно-технических специальностей и содержат рекомендации к работе над курсом высшей математики, программу курса с указанием литературы, примеры решения задач и двадцать вариантов контрольных заданий.
Ил. 6. Табл. 3. Библиогр.: 4 назв.
Рецензент д-р техн. наук М.Л. Лапшина Ответственный за выпуск зав. кафедрой д-р физ.-мат.
наук, проф. В.Д. Репников Печатается по решению редакционно-издательского со-
вета Воронежского государственного технического университета
©ГОУВПО «Воронежский государственный технический университет», 2008
2
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. Курс высшей математики разбит на темы и пункты, в которых указана литература, рекомендуемая для изучения теоретического материала, а также задачники с большим количеством разобранных задач.
Правильная организация процесса обучения является самым важным условием успешной проработки и усвоения учебного материала и, как правило, достаточна для своевременной защиты контрольных работ, а также сдачи зачетов и экзаменов. В связи с вышесказанным настоятельно советуется студентамзаочникам начинать изучение тем с проработки теоретического материала из соответствующих разделов рекомендованных учебников. При изучении теоретического материала по учебнику полезно конспектировать основные определения, формулировки теорем, формулы, уравнения и т.д.
Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь. В рекомендованных пособиях имеется большое количество подробно решенных задач, с которыми студентам необходимо ознакомиться при изучении соответствующего материала.
После изучения определенной темы по учебнику и решения достаточного количества задач рекомендуется воспроизвести по памяти определения, формулы, формулировки теорем. Хорошим подспорьем для объективной оценки степени освоения учебного материала является перечень вопросов для самопроверки, приведенный на странице 5-7.
Только после этого можно приступать к выполнению контрольных работ. На данном этапе полезно ознакомиться с примерными вариантами решения задач контрольной работы, приведенными в методических указаниях.
Зачет контрольной работы преподавателем осуществляется при выполнении следующих требований:
правильном и подробном решении задач в контрольной работе,
3
умении достаточно быстро и без помощи пособий решать задачи, аналогичные задачам, предложенным в контрольной работе,
твердом знании основных формул и определений, перечисленных в вопросах для самопроверки.
Если в процессе изучения теоретического материала или
при решении задач у студентов возникают вопросы, справиться с которыми самостоятельно не удается, то за помощью можно обратиться к преподавателю на консультации.
Завершающим этапом изучения отдельных частей курса высшей математики является сдача зачетов и экзаменов в соответствии с учебным планом.
Выбор варианта контрольной работы студентом производится по двум последним цифрам номера студенческого билета в соответствии со следующей таблицей.
Предпоследняя |
|
Предпоследняя |
|
цифра x совпадает с |
цифра x совпадает с |
||
Одной из цифр: |
|
одной из цифр: |
|
|
0, 2, 4, 6, 8 |
|
1, 3, 5, 7, 9 |
|
|
||
x1 - 1-й вариант |
x1 - 11-й вариант |
||
x2 - 2-й вариант |
x2 - 12-й вариант |
||
x3 - 3-й вариант |
x3 - 13-й вариант |
||
x4 - 4-й вариант |
x4 - 14-й вариант |
||
x5 - 5-й вариант |
x5 - 15-й вариант |
||
x6 - 6-й вариант |
x6 - 16-й вариант |
||
x7 |
- 7-й вариант |
x7 |
- 17-й вариант |
x8 |
- 8-й вариант |
x8 |
- 18-й вариант |
x9 |
- 9-й вариант |
x9 |
- 19-й вариант |
x0 |
- 10-й вариант |
x0 |
- 20-й вариант |
|
|
|
|
4
ПРОГРАММА КУРСА “ МАТЕМАТИКА” ДЛЯ СТУДЕНТОВ-ЗАОЧНИКОВ
ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ (ТРЕТИЙ СЕМЕСТР)
Числовые и функциональные ряды
1. Числовые ряды. Сходимость ряда [2, гл. 16, § 1].
2. Необходимые и достаточные признаки сходимости рядов с положительными членами [2, гл. 16, §§ 2,4,5,6].
3. Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость ряда [2, гл. 16,
§§ 7,8].
4. Степенные ряды. Теорема Абеля. Радиус сходимости степенного ряда [2, гл. 16, § 13].
5.Разложение функций в степенные ряды [2, гл.16, § 16]. 6. Тригонометрические ряды Фурье. Разложение функций
в ряд Фурье [2, гл. 17, §§ 1,2,4,5,6].
Кратные, криволинейные интегралы и интегралы по поверхности
7. Двойной интеграл, его свойства и вычисление.[2,
гл.14, §§ 1-3].
8. Вычисление площадей и объемов с помощью двойных интегралов. [2, гл.14, § 4].
9. Двойной интеграл в полярных координатах. [2,
гл.14, § 5].
10. Тройной интеграл. Вычисление тройного интеграла
(2, гл. 14, §§11,12).
11.Вычисление объема тела, применение тройных интегралов к задачам механики, физики (2, гл. 14, §§13,14).
12 Криволинейный интеграл и его вычисление. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования. [2, гл.15, §§ 1-4].
5
13. Поверхностный интеграл. Вычисление поверхностного интеграла. Формула Остроградского. [2, гл.15,
§§ 5-8].
Теория вероятностей и математическая статистика
14. Испытания и события. Относительная частота и вероятность случайного события. Формула классической вероятности. Статистическая вероятность. [4, гл.1, §§1-6].
15. Теоремы сложения вероятностей. [4, гл.2, §§1-3].
16. Условные вероятности. Теоремы умножения вероятностей. [4, гл.3, §§1-5].
17. Формула полной вероятности. Вероятность гипотез. Формула Байеса [4, гл. 4, §§ 1-9 ].
18. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа. [4, гл.5, §§1-3].
19. Случайные величины. Закон распределения вероятностей дискретной случайной величины. Функция распределения случайной величины. Биномиальное распределение, распределение Пуассона. [4, гл.6, §§1-5].
20. Математическое ожидание и дисперсия дискретной случайной величины. [4, гл.7, §§1-4, гл.8, §§ 1-5 ].
21. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. [4, гл.9, §§1-6].
22. Непрерывные случайные величины. Интегральная и дифференциальная функции распределения вероятностей. Закон равномерного распределения вероятностей. [4, гл.10, §§1-
3, гл.11, §§ 1-6 ].
23.Нормальное распределение. [4, гл.12, §§1-7].
24. Генеральная и выборочная совокупности. Эмпирическая функция распределения. Полигон и гистограмма. [4, гл.15,
§§1-8].
25. Статистические оценки параметров распределения. Генеральная и выборочная средняя. Генеральная и выборочная дисперсия. [4, гл.16, §§1-13].
6
26. Доверительный интервал и доверительная вероятность. [4, гл.16, §§14-17
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ требуется строгое соблюдение указанных ниже правил.
1.Контрольная работа выполняется в тетради в клетку чернилами любого цвета кроме красного. Необходимо оставлять поля для замечаний рецензента.
2.На обложке контрольной работы должны быть написаны фамилия и инициалы студента, шифр, название дисциплины, номер и вариант контрольной работы, адрес студента. В конце работы ставится дата ее выполнения и подпись студента
3.В работу включаются все задачи, указанные в задании,
истрого по положенному варианту.
4.Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
5.Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия.
6.После получения проверенной работы исправляются все отмеченные рецензентом ошибки и выполняются все рекомендации рецензента.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ К КОНТРОЛЬНОЙ РАБОТЕ № 3
1. Дайте определение сходящегося и расходящегося ря-
дов.
2. Сформулируйте необходимый признак сходимости ря-
дов.
3. Сформулируйте признаки Даламбера, Коши и интегральный признак сходимости рядов с положительными членами. Приведите примеры.
7
4.Дайте определение признака Лейбница сходимости знакочередующихся рядов. Приведите пример применения этого признака.
5.Сформулируйте теорему Абеля о сходимости степенных рядов. Выведите формулу радиуса сходимости ряда.
6.Что называется двойным интегралом от функции f(x,y) по области D? Укажите его геометрический смысл.
7.Что называется тройным интегралом от функции f(x,y,z) по области V? Укажите его геометрический смысл.
8.Сформулируйте основные свойства двойного и тройного интегралов.
9.Что называется двукратным интегралом от функции f(x,y) по области D и как он вычисляется?
10.Запишите формулу для вычисления двойного интеграла с помощью двукратного.
11.Запишите формулы для вычисления тройного интеграла в цилиндрических и сферических координатах
12.Где используются кратные интегралы?
13.Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?
14.Дайте определение суммы и произведения событий.
15.Сформулируйте теоремы сложения и умножения вероятностей.
16.Запишите формулу полной вероятности.
17.Приведите формулу Байеса.
18.Дайте определение последовательности независимых испытаний. Запишите формулу Бернулли.
19.Дайте определение случайной величины.
20.Дайте определение функции распределения и плотности распределения случайной величины. Сформулируйте их свойства. Приведите примеры.
21.Дайте описание дискретных и непрерывных распределений: равномерное, биномиальное, нормальное.
8

22. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному или равномерному закону.
РЕКОМЕНДУЕМЫЕ ЗАДАЧИ ДЛЯ ПОДГОТОВКИ
КВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 3
Кзадаче № 1. [2] 296-299, 301,302, 304-310, 311-315, 316-328, 368-377.
Кзадаче № 2. [2] 17-25.
Кзадаче № 3. [2] 55-65.
К задаче № 4. [4] 89, 90, 91, 97, 98, 105, 106-108.
Кзадаче № 5. [4] 165-171, 174, 188210, 213-217.
Кзадаче № 6. [4] 252-274, 280, 281, 292-298.
Кзадаче № 7. [4] 443449.
Кзадаче № 8. [4] 501512, 515-322.
Контрольная работа № 3 «Числовые и функцииональные ряды. Кратные интегралы. Теория вероятностей и элементы математической статистики»
Задача № 1.
Найти интервал сходимости степенного ряда.
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||
1. |
|
|
|
|
|
xn |
11. |
|
|
xn |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n1 |
|
n |
|
n 1 |
n(n 1) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
3n |
|
|
|
|
|||||||
2 . |
|
|
|
|
|
xn |
12. |
|
|
|
xn |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n 1 |
|
|
3n 2 |
|
n 1 |
|
|
3 n |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
|
|
|
xn |
|
|
|
|
13. |
|
|
|
|
n |
xn |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n 1 |
|
nn |
|
|
|
|
|
n 1 |
|
|
n! |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|||||||||
4. |
|
xn |
14. |
|
|
|
|
|
|
|
xn |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n 1 |
|
|
n! |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
(2n 1)3 |
|
|
|||||||||||
9
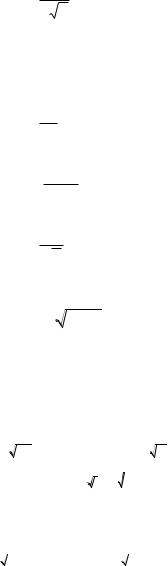
5. n 1
6. n 1
7. n 1
8. n 1
9. n 1
10. n 1
n 1n xn
|
1 |
xn |
|
|
|
n |
2 n |
|
3 |
|
n2 xn n!
(n!)2 x n (2n)!
10n xn 
 n
n
|
1 |
xn |
|
|
|
||
2n |
|
||
2n 1 |
|||
|
15.
n 1
16.
n 1
17.
n 1
18.
n 1
19.
n 1
20. n 1
|
|
n2 |
|
|
|
|
|||
|
|
|
|
xn |
|
|
|||
|
|
|
|
|
|
||||
n 1 |
|
|
|
|
|||||
|
|
|
2n |
|
|
xn |
|||
|
|
|
|
|
|
|
|||
n(n 1) |
|||||||||
|
|
||||||||
|
|
|
n 2 |
|
xn |
||||
|
|
|
|
|
|
|
|
||
(n 3)3n |
|||||||||
|
|||||||||
|
|
|
n4 |
|
|
|
xn |
||
|
(n 1)n |
|
|||||||
|
|
|
|||||||
|
|
(n 1)2 |
|
xn |
|||||
|
|
|
2n |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
7n |
|
|
|
xn |
||
|
|
|
5n |
3n |
|
||||
|
|
|
|
|
|||||
Задача № 2.
Изменить порядок интегрирования.
|
1 |
|
0 |
|
|
|
0 |
|
|
0 |
|
|||||
1. |
dy |
|
|
|
f (x, y) dx |
dy |
|
f (x, y) dx . |
||||||||
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
2 y |
y |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y |
|
|
|
|
|
|
|
2 y2 |
||||||
|
1 |
|
|
|
|
2 |
|
|||||||||
2. dy f (x, y) dx dy |
|
|
f (x, y) dx . |
|||||||||||||
|
0 |
0 |
|
|
|
|
1 |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
y |
2 |
|
2 y |
|
|
|
|
|||||
3. |
dy |
f (x, y)dx dy f (x, y)dx . |
||||||||||||||
|
0 |
|
0 |
|
|
1 |
0 |
|
|
|
|
|||||
10
