Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matem_342-2008

.pdf

Скачиваний:

Добавлен:

26.03.2016

Размер:

757.08 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

l = lim

un1

lim

(n 1)2

(3n)!

n (3n 3)!n2

= lim

(n 1)2

= 0 < 1.

n n2 (3n 3)(3n 2)(3n 1)

По признаку Даламбера данный ряд сходится.

Пример 2.

Исследовать сходимость числового ряда

n(ln n)2

n 2

Решение.

Введем функцию

f (x) =

, удовлетво-

x ln 2 x

ряющую условиям

f (n)

исследуем сходи-

n ln

2 n

мость, используя интегральный признак. Для этого вычислим

lim

= lim

d (ln x)

x(ln x)2

(ln x)2

= lim

lim

ln x

ln 2

ln b

ln 2

Несобственный интеграл сходится, следовательно, сходится и данный ряд

Пример 3. Найти интервал сходимости степенного ряда

	1
	1	x n .

	3n n2
n 1

Решение. Составим ряд из модулей членов данного ряда

x n

un1

и вычислим

l =

lim

3n n2

n 1

= lim

3n1(n 1)2

По признаку Даламбера

ряд

сходится при l < 1, от-

сюда

< 1 или |x| < 3.

Следовательно, ряд абсолютно сходится

при x (-3,3). Исследуем сходимость ряда

в граничных точ-

ках. При x =3

и x = -3 из данного ряда получаем соответствен-

( 1)n

но числовые ряды

Из интегрального

n 1

признака сходимости следует, что эти ряды сходятся абсолютно, поэтому интервалом сходимости данного ряда является промежуток [-3,3].

Пример 4. Определить пределы интегрирования интегра-

ла f x, y dxdy , если область интегрирования S		(рис. 1)
S
ограничена гиперболой y2 x2	1 и двумя прямыми	x 2 и

x 2 (имеется в виду область, содержащая начало координат).

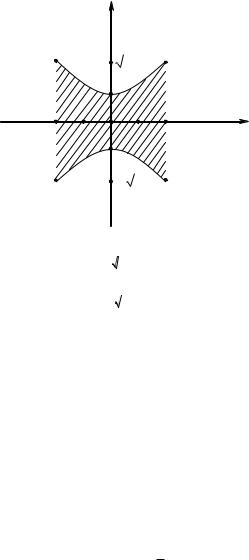
Решение. Область интегрирования ABCD (рис. 1) ограничена прямыми x 2 и x 2 и двумя ветвями параболы:

y 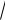1 x2 и y 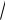1 x2 .

									у

						C
																D
								1				5				D





										S									х

					-2				0								2
					-2				0								2
								-1
								-1


												5
						A						5					B

								Рис. 1



							2			1 x2
f x, y dxdy dx															f x, y dy
S							2
S							2				1 x		2
											1 x
Пример 5. Вычислить двойной интеграл I ex y dxdy ,
																				D
где D – прямоугольник: 0 x 1;0 y 2
Решение.
	1		2				1					2					1		ex dx ex 2 ex 1
I		dx		ex y dy				ex y				2		dx				ex 2	ex dx ex 2 ex 1
												0									0
	0		0				0										0
e1 2 e1 e2 e0 e3 e2
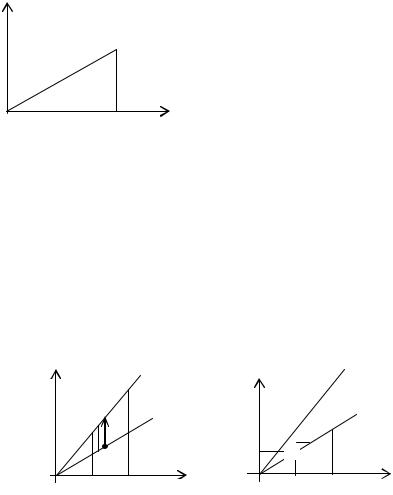
Пример 6. Вычислить двойной интеграл:																				I	xy2 dxdy,
																				D

где D – треугольник y 0, x 2; y 2x

у									x								x
				2									2
				2		2							2				2
		I xdx xy2 dy xdx y2 dy
у=х/2				0		0							0				0
				y				x					x
	2				3		2				2			3
	x						2			dx x						dx
0

	0			3			0				0		24
													24
у=0
	х		2								5	2
	х
		1								1 x					4
		1	x4dx							1 x					4
Рис. 2.			x4dx
Рис. 2.	24 0									24 5		0		15
														15

Пример 7. Поменять порядок интегрирования:
I f (x, y)dxdy ,	где D: x=1, x=2, y=x; y=2x.
D

Решение.

x=у/2

у=2х

у=х

				1	2
0	1	2	х	0	1	2	х
	1	2	х	0	1	2	х
				Рис. 3.

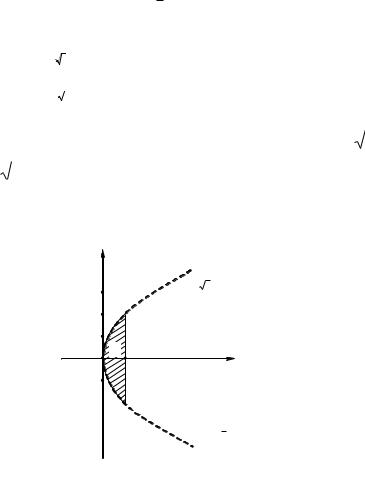
2	2 x
I dx		f (x, y)dy
1	x	D1	D2
2	y	4 2

dy f (x, y)dx dy f (x, y)dx

1 1 2 y

Пример 8. Изменить порядок интегрирования в двойном интеграле:


	1	2	x
I dx					f x, y dy
	0	2		x
Решение. Зная пределы интегрирования, найдем границы
	интегрирования D: x 0 ,					x 1,
области	интегрирования D: x 0 ,					x 1,	y 2 x ,
y 2
y 2	x и построим их (рис. 4). Область D располагается в

полосе 0 x 1 и ограничена сверху и снизу соответствующими ветвями параболы y2 4x

		у 2 х
2	B
	D	x
0	1	x
0	1

-2 A

у 2х

Рис. 4

Найдем новые пределы внешнего (по у) и внутреннего (по х) интегрирования. Так как область D проецируется на ось Оу в отрезок АВ, то пределами внешнего интегрирования являются ординаты точек А и В, т. е.

x 1. Та-

y 2 и y 2 соответственно. Левой границей области

является кривая x	y 2	(уравнение параболы y2 4x

4

разрешено относительно х), а правой – прямая

ким образом, двойной интеграл I с измененным порядком интегрирования запишется в виде

				2		1
			I dy f x, y dx .
				2			y2
						4
			Пример 9. Вычислить интеграл
	1			1
I dx x y dy
	0			x
		1 1								1	1			1				1		1					1
I x y dy dx											xdy ydy dx x									dy					ydy		dx
		0 x								0 x				x				0		x					x
1					y2			1		1		2		1		x2			1			3		2				1
1					y2			1		1		2		1		x2			1			3		2				1
	xy							dx	x x								dx						x		x				dx
	xy							dx	x x								dx						x		x				dx
0					2			x		0				2 2					0			2						2
0					2			x		0				2 2					0			2						2
	3		1			1			1	1			3		x3		x2	1							1	1			1	1
	3		1			1			1	1			3		x3		x2	1			1				1	1			1	1
			x2dx xdx							dx									x												.
			x2dx xdx							dx									x												.
	2		0			0			2	0			2 3 2					2			0				2 2 2 2
	2		0			0			2	0			2 3 2					2			0				2 2 2 2
			Пример 10.
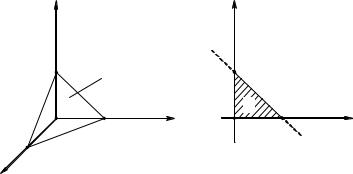
			Вычислить объем тела, ограниченного поверхностями
x 0 ,				y 0 ,				z 0 ,		x y z 1 с помощью тройного инте-

грала.

Решение. Данное тело изображено на рис. 5. На рис. 6 изображена проекция этого тела на плоскость Оху.

x+y+z=1		1	x+y=1
			x+y=1
			D
1	y	0	1	х
1		0	1

1
x
Рис. 5	Рис. 6

V= dxdydz , где (V) – область, ограниченная поверхностя-

ми x 0 , y 0 , z 0 (координатные плоскости), x y z 1

(плоскость, отсекающая на координатных осях отрезки, равные 1), т. е. область (V) есть пирамида. Из чертежа видно, что по любой из переменных можно с одинаковым успехом брать постоянные пределы, и они равны 0 и 1. Возьмем, например, постоянные пределы по х ( 0 õ 1). Проекцией пирамиды на плоскость Оху является треугольник, ограниченный прямыми x 0 , y 0 и x y 1 (рис. 6). Отсюда определяем пределы интегрирования по у ( 0 ó 1 õ ). Для переменой z нижним пределом будет, очевидно, z 0 (плоскость Оху), а верхним – значение z, полученное из уравнения плоскости

x y z 1, т. е. z 1 x y .

Определив пределы интегрирования по каждой переменной, можем представить данный тройной интеграл через повторный и вычислить объем тела:

		1			1 x					1 y x							1		1 x			1 y x
		1			1 x					1 y x							1		1 x			1 y x
V dx							dy						dz dx z													dy
		0				0					0						0		0					0
		0				0					0						0		0
1				1 x														1			y	2						1 x
1				1 x														1			y	2						1 x
dx						1 y x dy y																	xy						dx
dx						1 y x dy y															2		xy						dx
0					0									2				0											0	1		x
0					0													0											0
1																								1									2
1 x								1 x							x 1 x dx 1 x																x			x x2 dx
1 x															x 1 x dx 1 x																x			x x2 dx
											2														0					2		2
0											2														0					2		2
1			1						x2							1		1		1						1	1
					x							dx						dx xdx									x2dx
					x							dx						dx xdx									x2dx
0			2						2							2		0		0						2	0
	1						x2				x3						1		1		1			1		êóá. åä
	1						x2				x3				1		1		1		1			1
				x
	2			x		2					6						2		2		6			6
															0
															0
				Пример 11. В первой урне 2 белых и 3 черных шара, во

второй - 7 белых и 1 черный. Из первой урны в первую переложили 2 шара, затем наудачу извлекли шар из второй урны. Найти вероятность того, что выбранный из второй урны шар - белый.

Решение. Если событие А может произойти только совместно с одним из событий Н1 , Н2 , ..., Н k , образующих пол-

ную группу несовместных событий (гипотез), то вероятность Р(А)появления события определяется по формуле полной веро-

k
ятности: Р (А) = Р(H i )	Р(А/H i ), где Р(H i ) - вероят-
i 1
ность гипотезы H i , Р(А/H i )	- условная вероятность события
А при этой гипотезе.

Вероятность извлечения белого шара из второй урны после добавления двух шаров из первой урны зависит от состава шаров (по цвету) в этой урне. При этом возможны следующие гипотезы:

Н1 - из первой урны во вторую переложены два белых

шара,

Н2- из первой урны во вторую переложен один белый и один черный шар,

Н3 - из первой урны во вторую переложены два черных

шара.

Найдем вероятности этих гипотез . Вероятность каждой гипотезы связана с вероятностью извлечения соответствующих шаров из первой урны. Тогда получим

1 2! 3!

Р (Н1 )

= 0,1,

C 2

C1C1

2! 3! 2! 3!

Р (Н2) =

2 3

= 0,6,

C 2

1! 1! 1!

2! 5!

3! 2! 3!

Р (Н3)

= 0,3.

C 2

2! 1! 5!

Пусть А - событие, состоящее в извлечении белого шара из второй урны, если предварительно имела место одна из гипотез Нi. Условные вероятности события А будут :

Р(А/H1) = 9/10, Р(A/Н2) = 8/10, Р(A/Н3) = 7/10.

По формуле полной вероятности найдем вероятность извлечения белого шара из второй урны

Р(А) = Р(H1) Р(А/H1) + Р(H2) Р(А/H2) + Р(H3) Р(А/H3) =

= 0,1 0,9 + 0,6 0,8 + 0,3 0,7 = 0,78.

Пример 12. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5, для третьего - 0,8. Мишень не поражена. Найти вероятность, что выстрелы произведены первым стрелком.

Решение. Если вероятности гипотез до опыта были Р (Н1), Р (Н2) , ..., Р(Н n ), а в результате опыта появилось со-

бытие А , то условная вероятность Р(Н k /A) с учетом появления события А вычисляется по формуле Бейеса:

Р(Н k /A) =	P(Hk )P( A / Hk )
Р(Н k /A) =	n
	P(Hi )P( A / Hi )
	i1

Возможны три гипотезы: H1 - на линию огня вызван первый стрелок; H2 - на линию огня вызван второй стрелок; H3 - на линию огня вызван третий стрелок. Так как вызов на линию огня любого стрелка равновозможен, то вероятности этих

гипотез до опыта Р(H1) = Р(H2) = Р(H3) = 1/3.

В результате опыта наблюдалось событие А - после произведенных двух выстрелов мишень не поражена. Условные вероятности этого события

Р(А/H1) = 0,7 0,7 = 0,49; Р(А/H2) = 0,5 0,5 = 0,25; Р(А/H3) = 0,2 0,2 = 0,04.

По формуле Бейеса для частного случая, когда вероятности гипотезы опыта равны между собой, находим вероятность гипотезы Н1 после опыта:

Р(H1/A) =	0,49		0,49	= 0,628
	0,25	0,04	0,78
0,49

Пример 13. Вероятность попадания в цель у стрелка р = 0,8. Производится три выстрела. Построить ряд распределения случайной величины Х – числа попаданий в цель. Найти математическое ожидание М [X] и дисперсию D [X].

Решение. Случайная величина Х может принимать значения : 0, 1, 2, 3. Вероятность того, что попаданий не будет

р (х=0) найдем по формуле Бернулли				P	n	(k) =	Ck pk q n k	,
					n		n
здесь p = 0,8, q = 1- p= 0,2, n = 3, k = 0.
p (x=0) =	C0 0,80 (1 0,8)3	=	3!	0,800, 23			= 0,008.


	3		3!0!
			3!0!

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.05.2015325.63 Кб154L_r_5.doc
#
31.05.201562.98 Кб65L_r_7.doc
#
31.05.2015279.55 Кб76L_r_8.doc
#
31.05.2015194.05 Кб79L_r_9.doc
#
31.05.20158.34 Mб27manual-samsung-galaxy-note-3-n9000.pdf
#
26.03.2016757.08 Кб9matem_342-2008.pdf
#
31.05.20152.94 Mб14met1end.doc
#
26.03.2016119.81 Кб7metallorezh-stanki_metodichka.doc
#
31.05.2015771.21 Кб9MetEccess.pdf
#
31.05.20152 Mб13Metodicheskie_ukazania_1_po_informatike_2002.doc
#
31.05.20152.25 Mб342Metodicheskoe_posobie_TSOIB.doc