1.17.Основные теоремы о пределах
Теорема
. Для того чтобы
последовательность 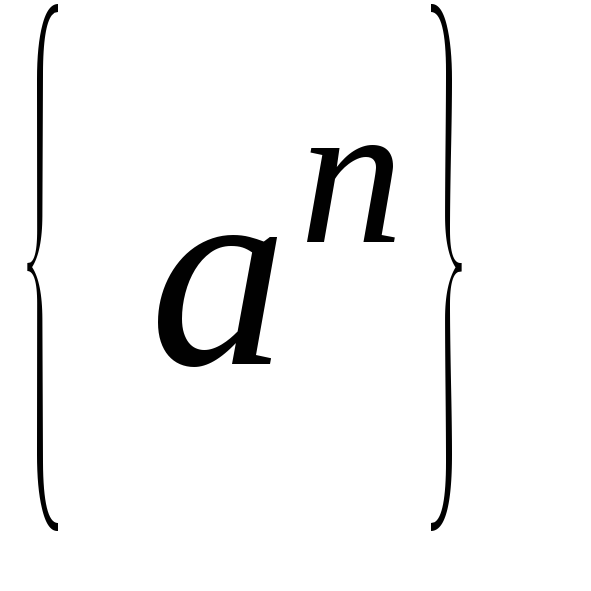 имела пределом число А необходимо и
достаточно, чтобы она была представима
в виде
имела пределом число А необходимо и
достаточно, чтобы она была представима
в виде 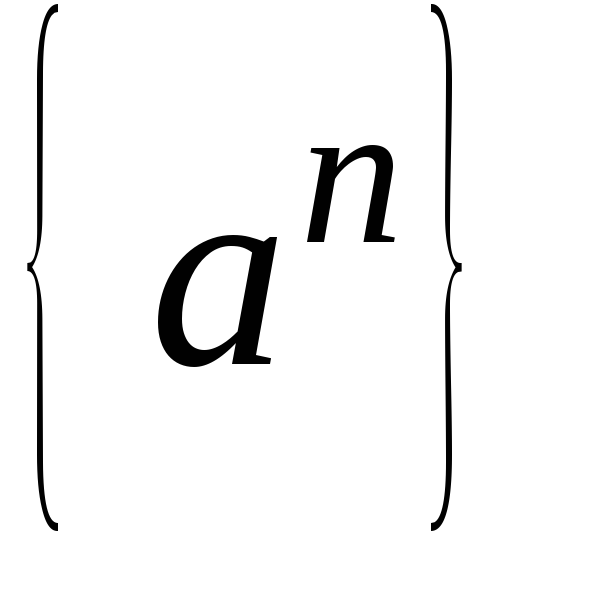 =
А+
=
А+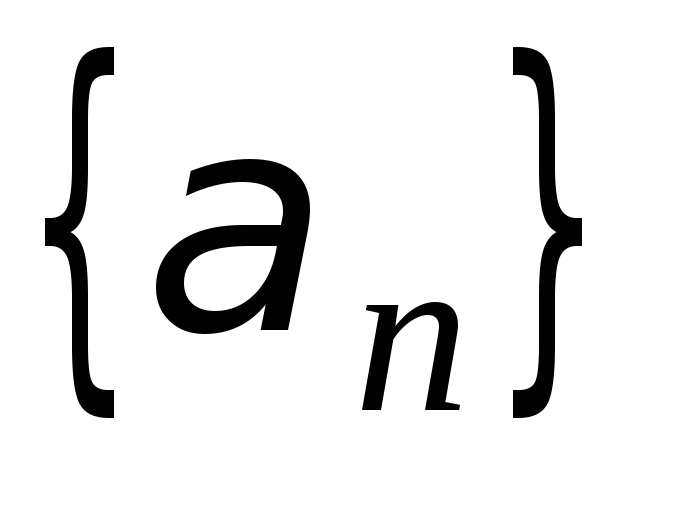 ,
где
,
где 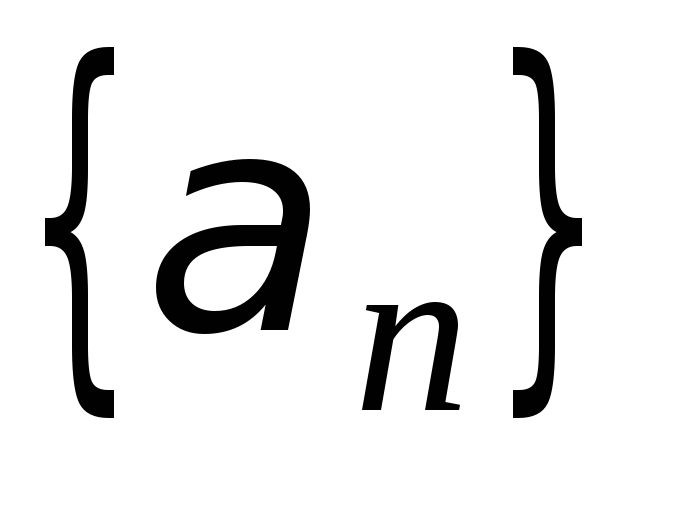 -
-
бесконечно
малая последовательность.
Теорема 1.
Пусть 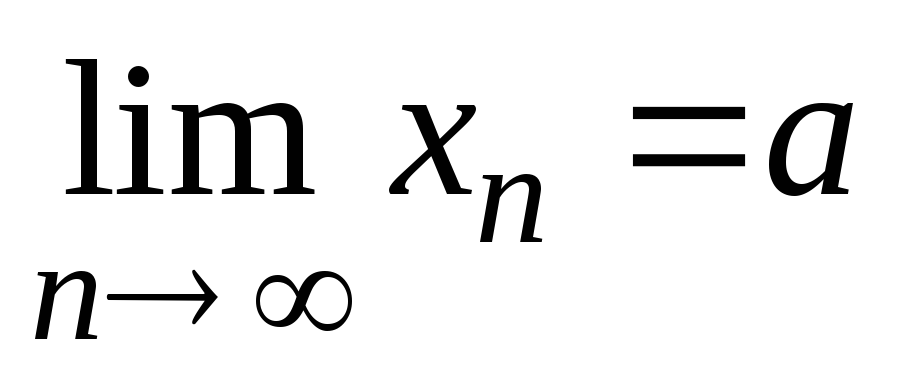 и
и 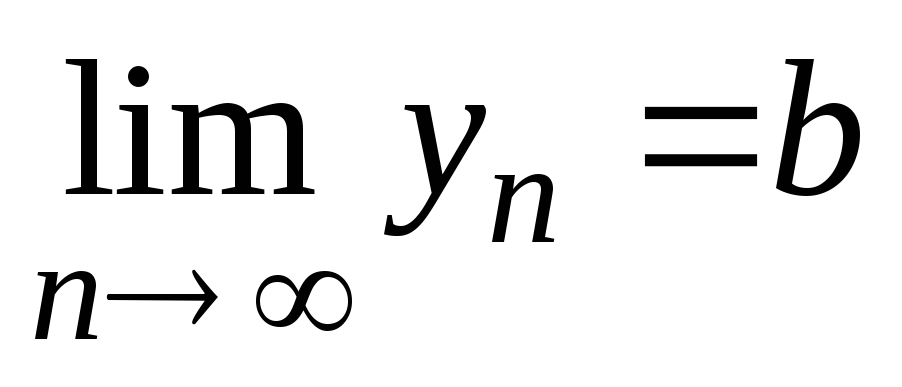 .
Тогда:
.
Тогда:
а)
 ;
;
б)
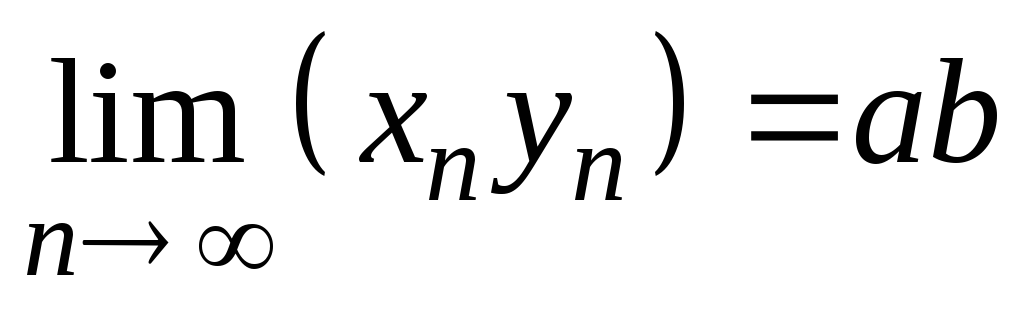 ;
;
в)
если 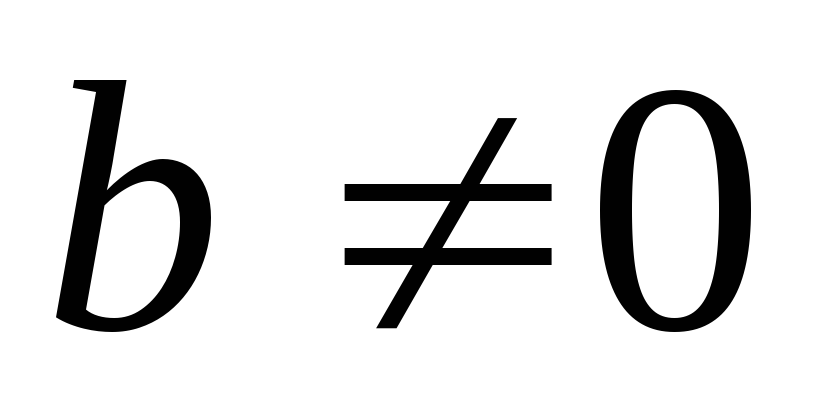 ,
то начиная с некоторого номера определена
последовательность
,
то начиная с некоторого номера определена
последовательность 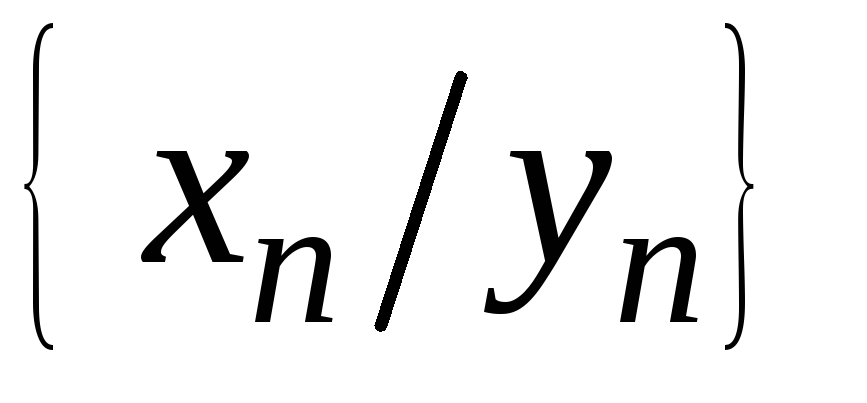 и
и 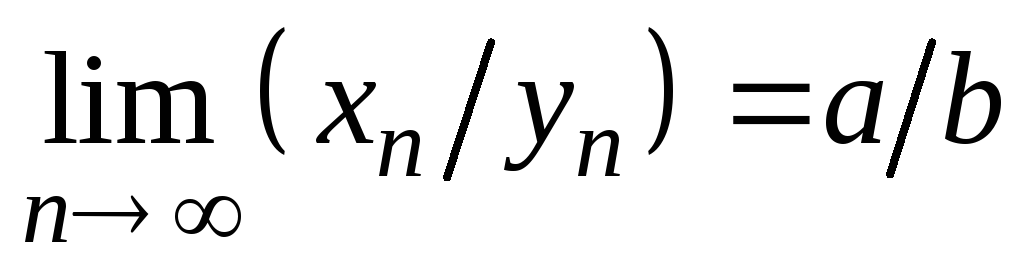 .
.
Если
 ,
то
,
то 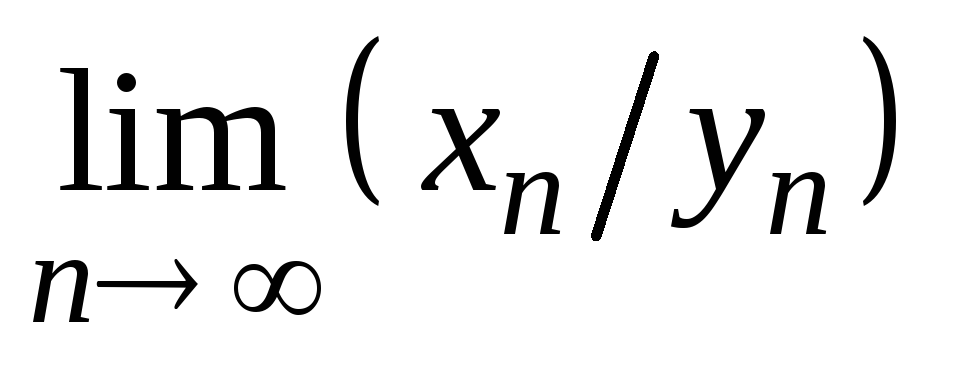 называют неопределенностью
типа
называют неопределенностью
типа 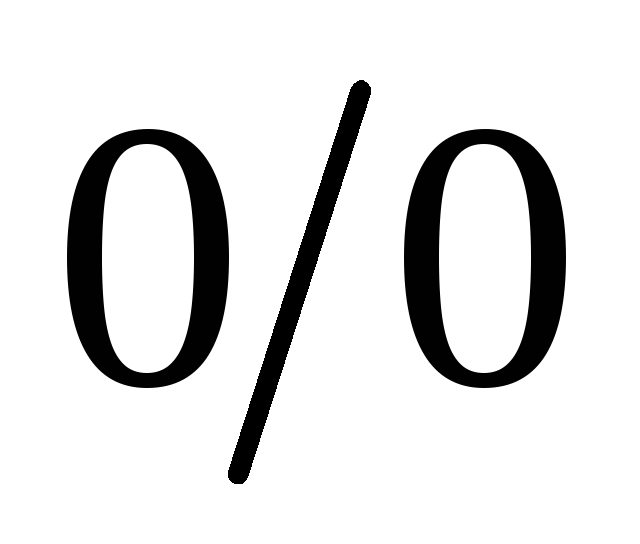 .
Аналогично определяются неопределенности
типа
.
Аналогично определяются неопределенности
типа 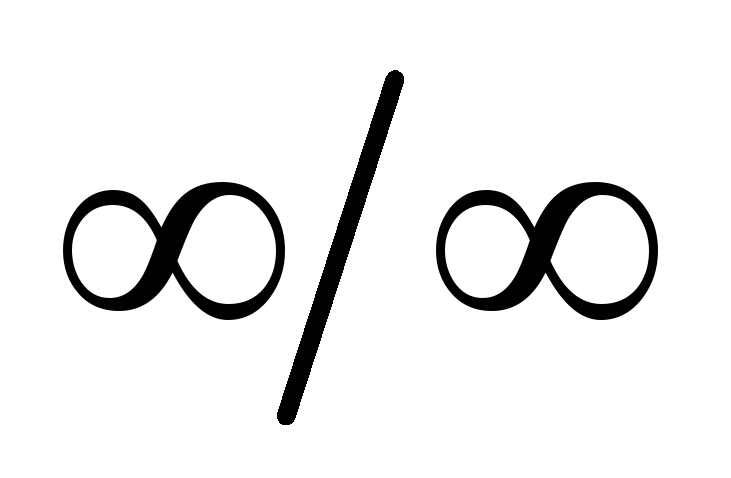 ,
,
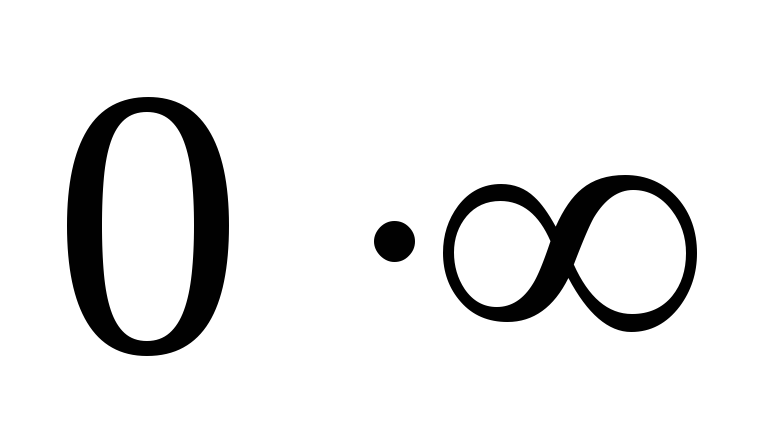 ,
,
 .
В этих случаях теорема 1 неприменима.
.
В этих случаях теорема 1 неприменима.
1.
Доказать, что (указать
(указать ).
).
1)
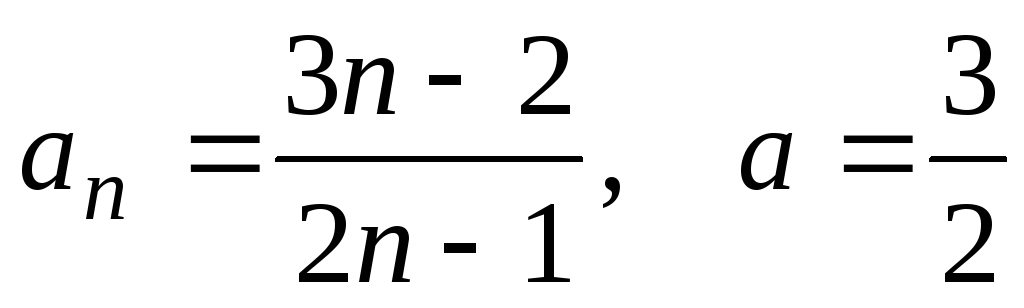 ;
2)
;
2)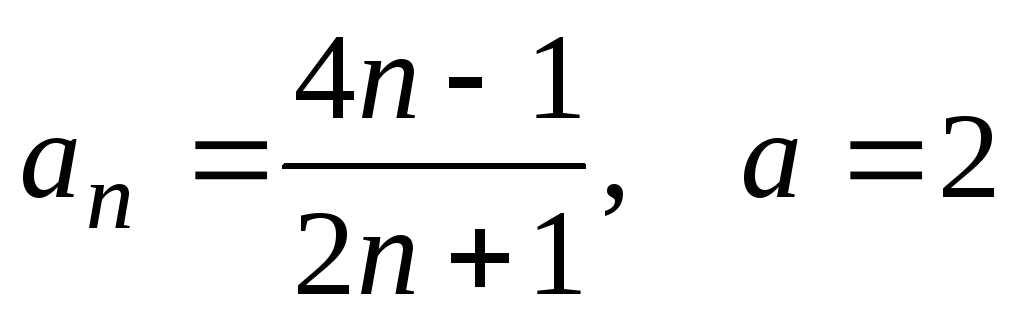 ;
;
3)
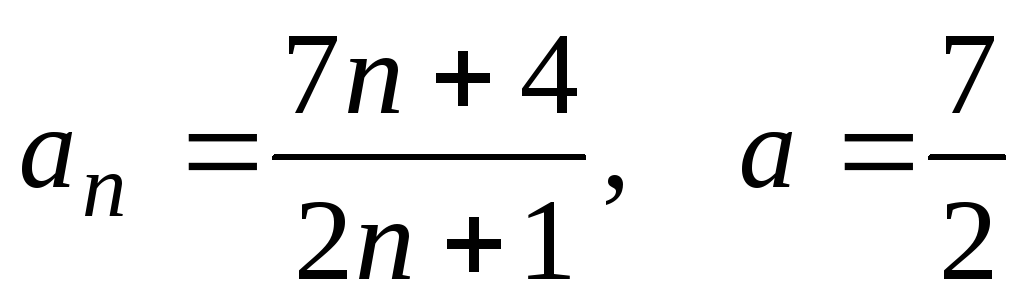 ;
4)
;
4)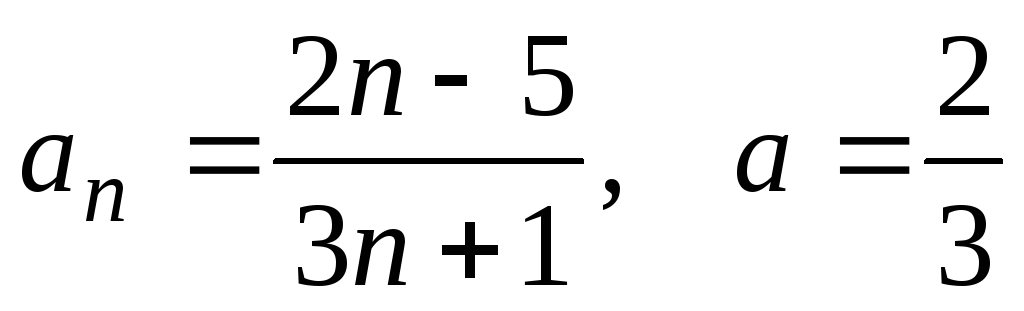 ;
;
5)
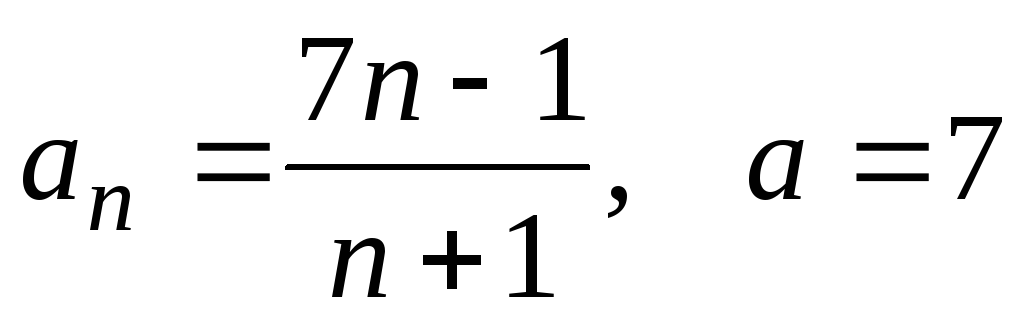 ;
6)
;
6)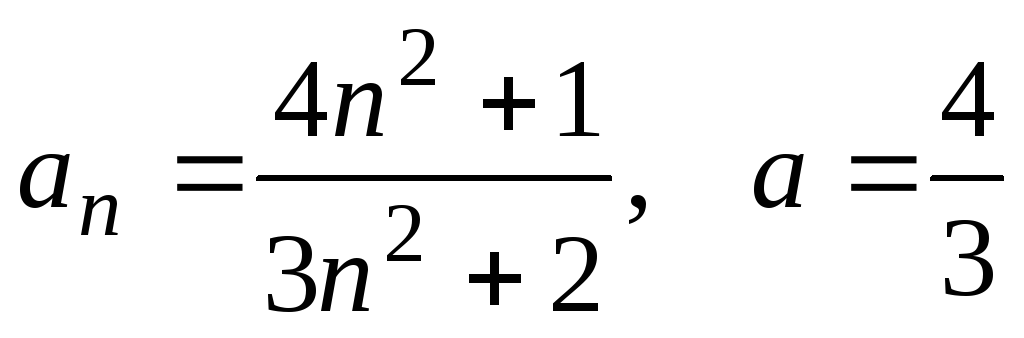 ;
;
7)
 ;
8)
;
8)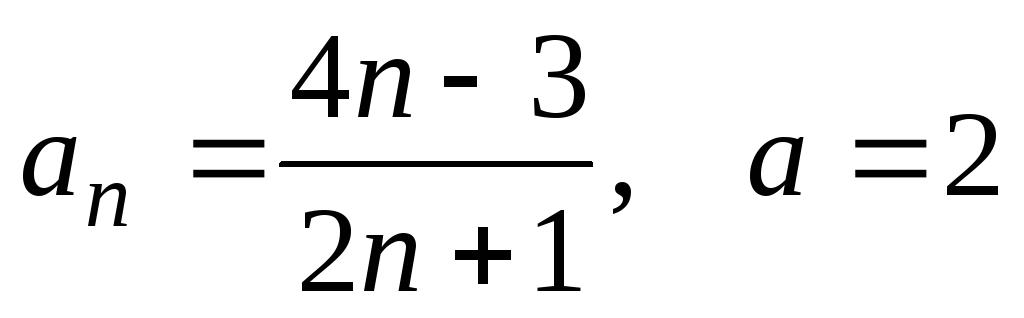 ;
;
9)
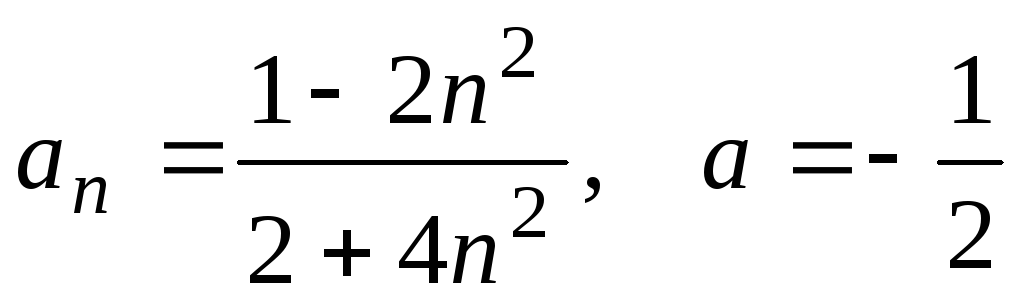 ;
10)
;
10) .
.
2.
Доказать ограниченность или
неограниченность последовательностей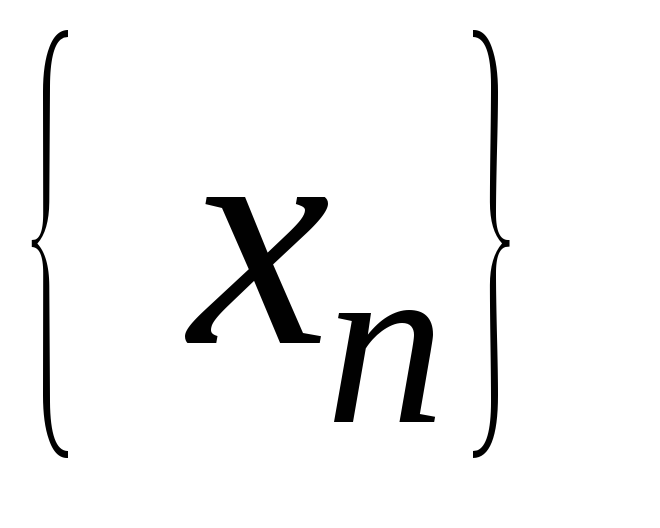 .
.
1)
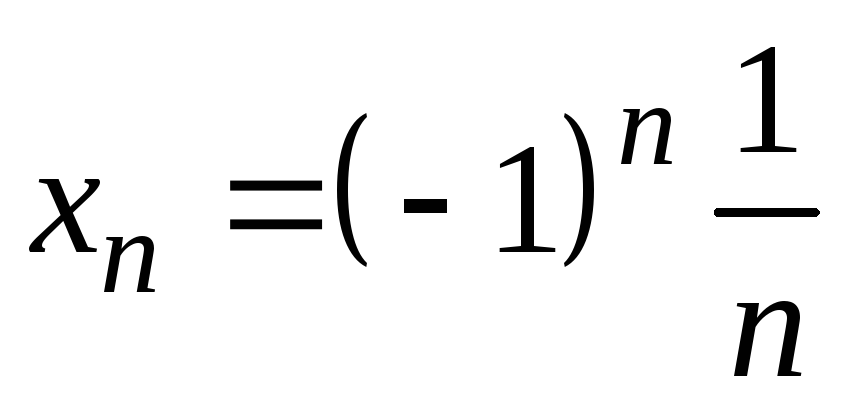 ;
2)
;
2) ;
3)
;
3)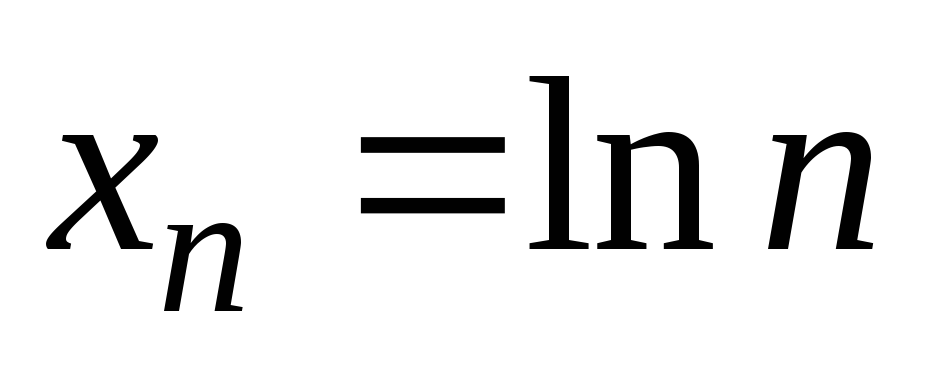 ;
4)
;
4)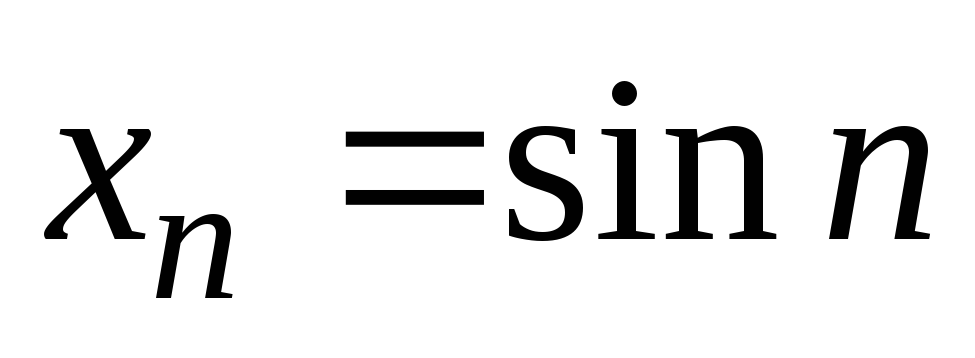 ;
;
5)
 ;
6)
;
6)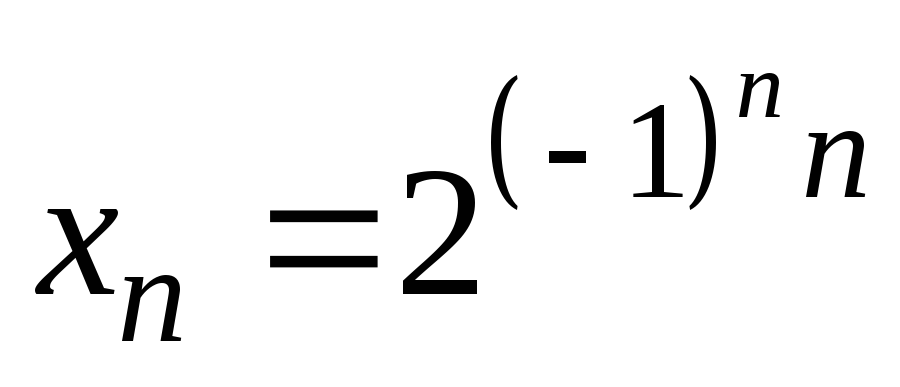 ;
7)
;
7) ;
;
8)
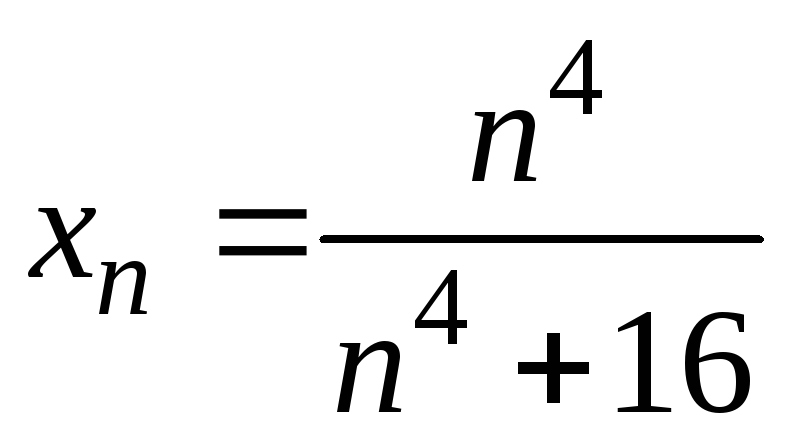 ;
9)
;
9)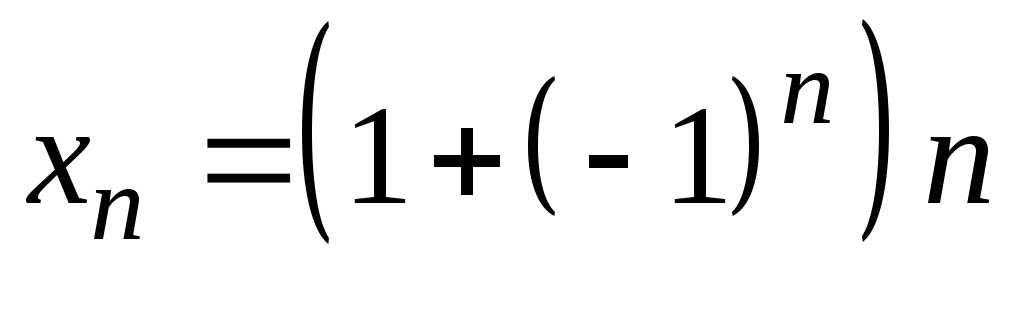 ;
10)
;
10)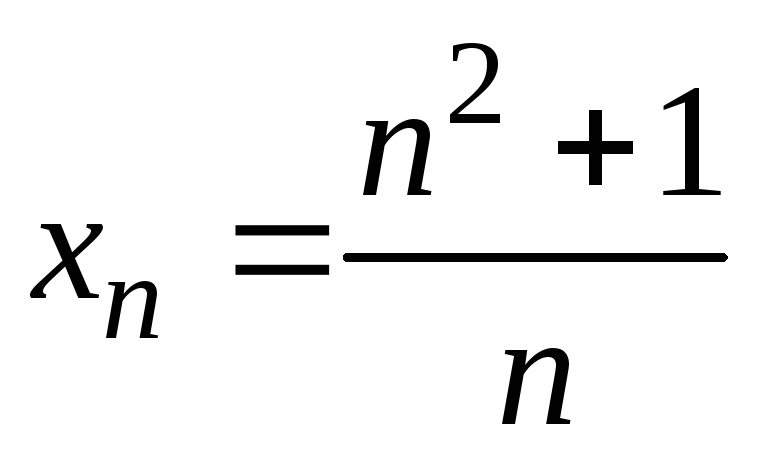 .
.
3.
Установить, являются ли последовательности бесконечно большими, бесконечно малыми
или не являются ни бесконечно большими,
ни бесконечно малыми.
бесконечно большими, бесконечно малыми
или не являются ни бесконечно большими,
ни бесконечно малыми.
1)
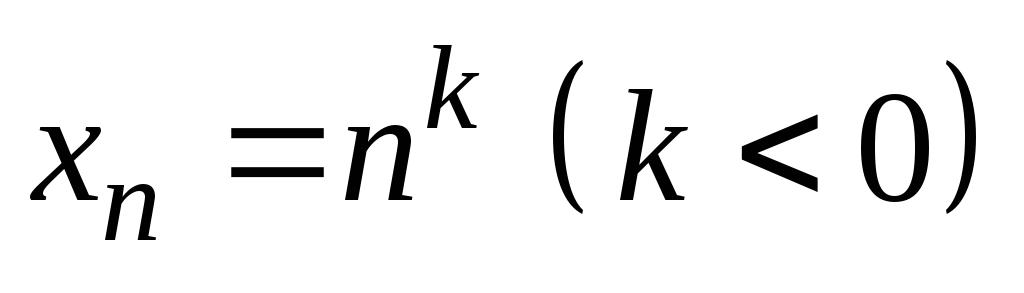 ;
2)
;
2) ;
3)
;
3)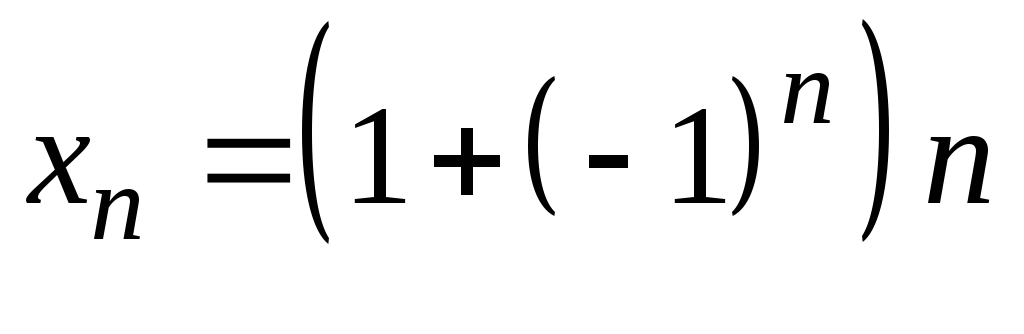 ;
;
4)
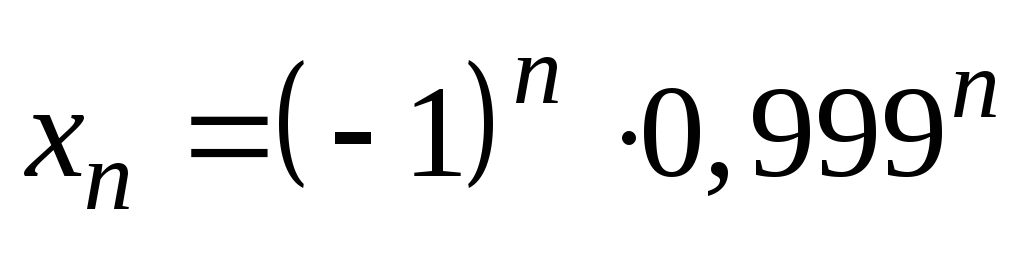 ;
5)
;
5)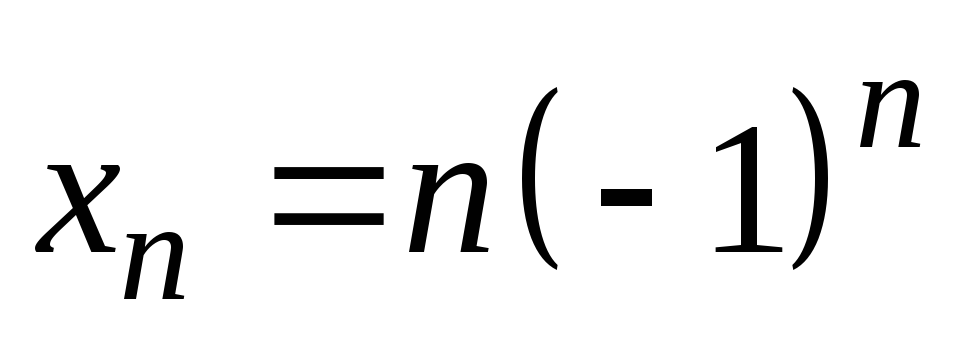 ;
6)
;
6)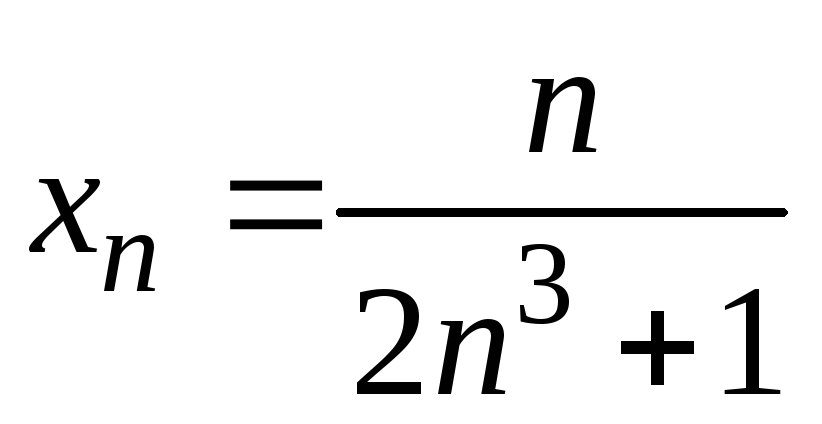 ;
;
7)
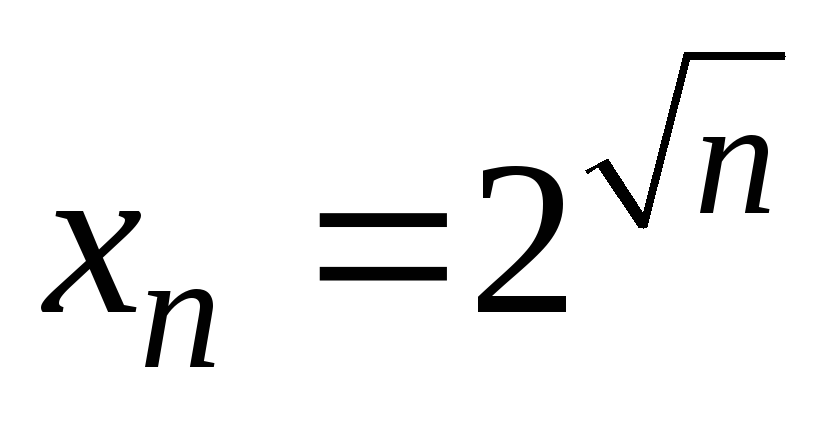 ;
8)
;
8) ;
;
9)
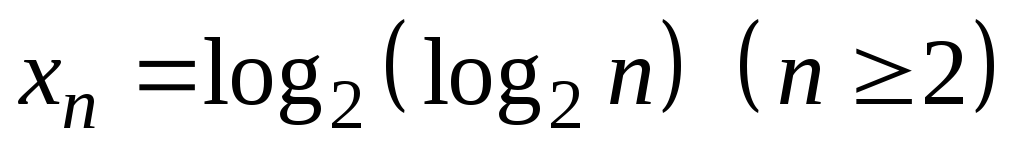 ;
10)
;
10)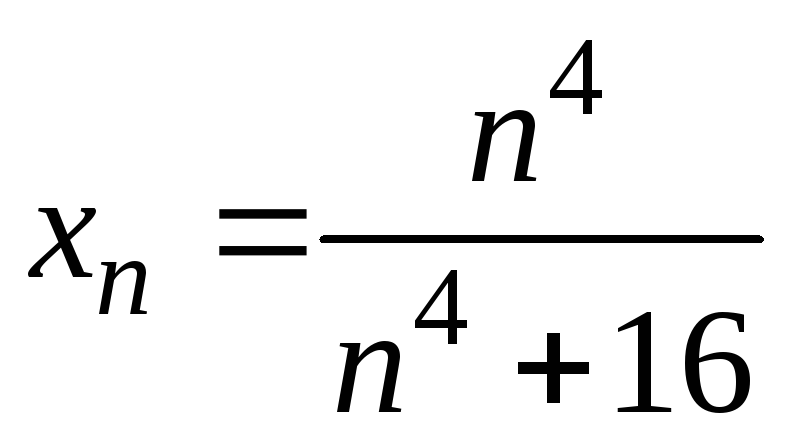 .
.
4.
Вычислить пределы числовых
последовательностей.
1)
 ;
2)
;
2) ;
;
3)
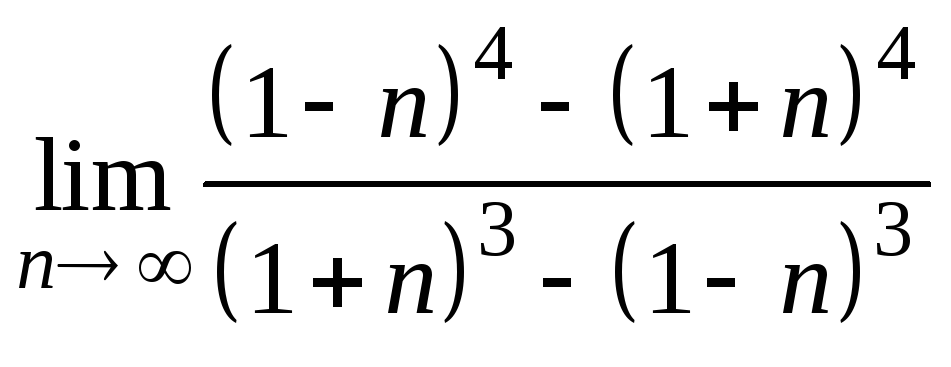 ;
4)
;
4)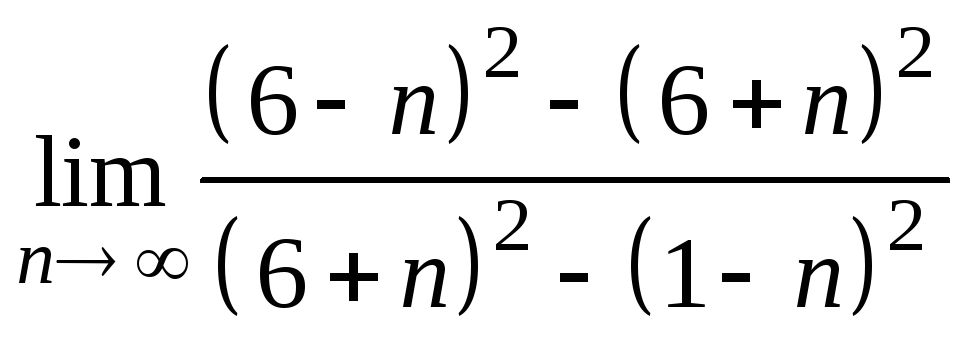 ;
;
5)
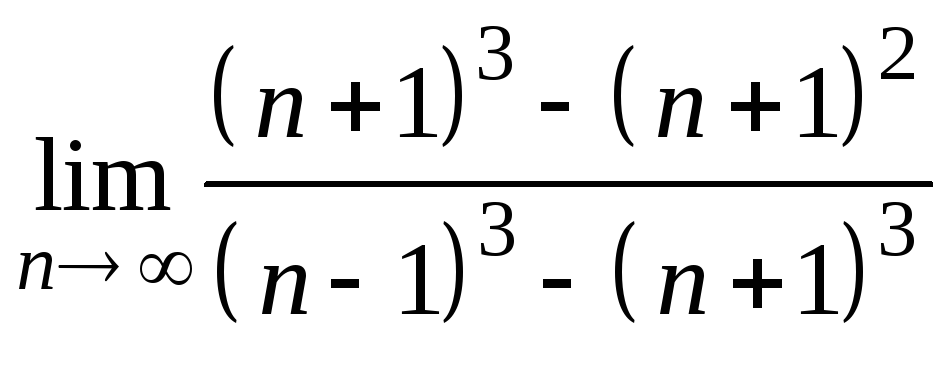 ;
6)
;
6)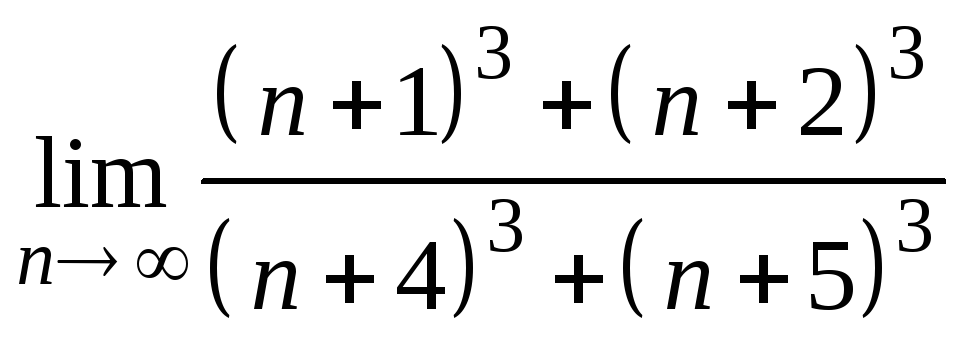 ;
;
7)
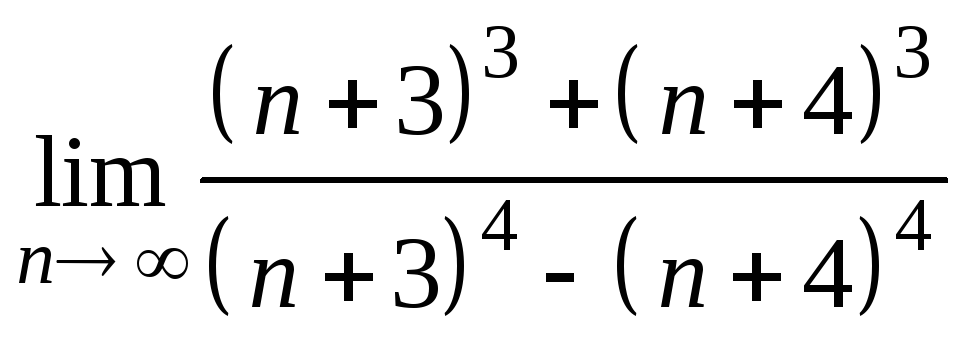 ;
8)
;
8) ;
;
9)
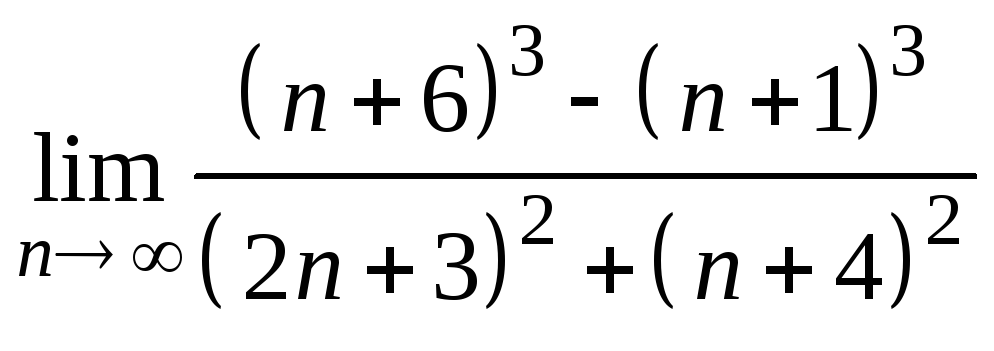 ;
10)
;
10)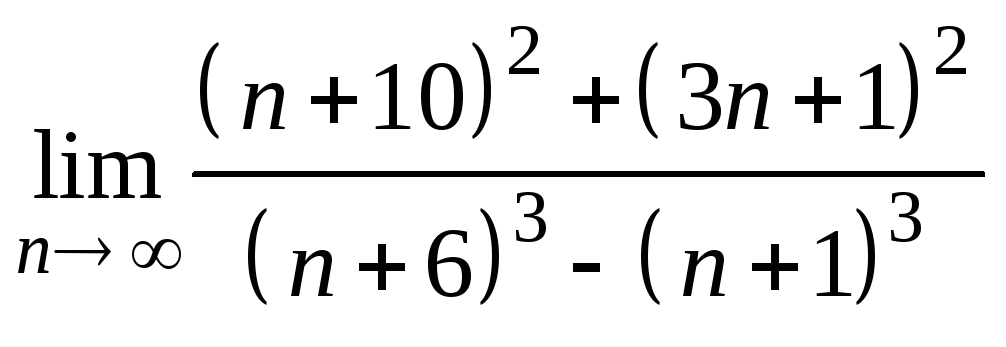 .
.
5.
Вычислить пределы числовых
последовательностей.
1)
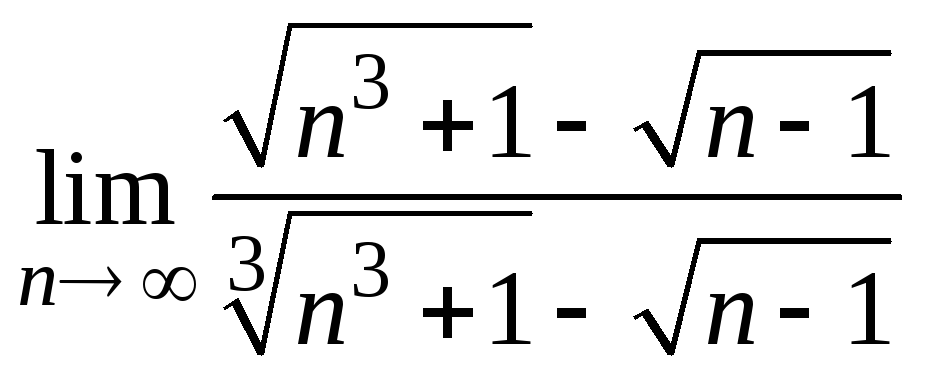 ;
2)
;
2)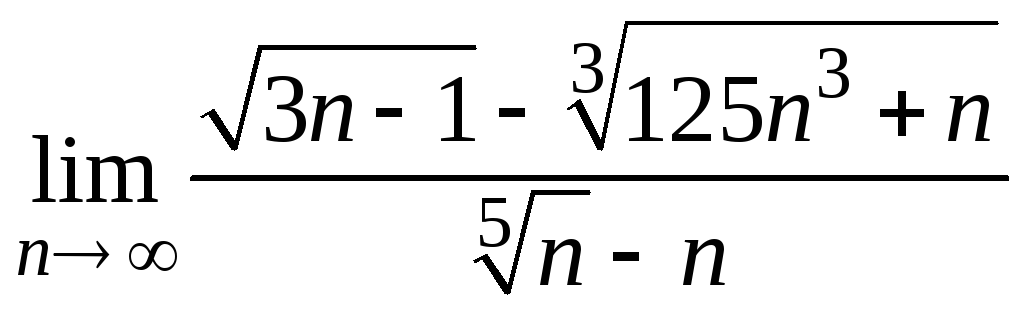 ;
;
3)
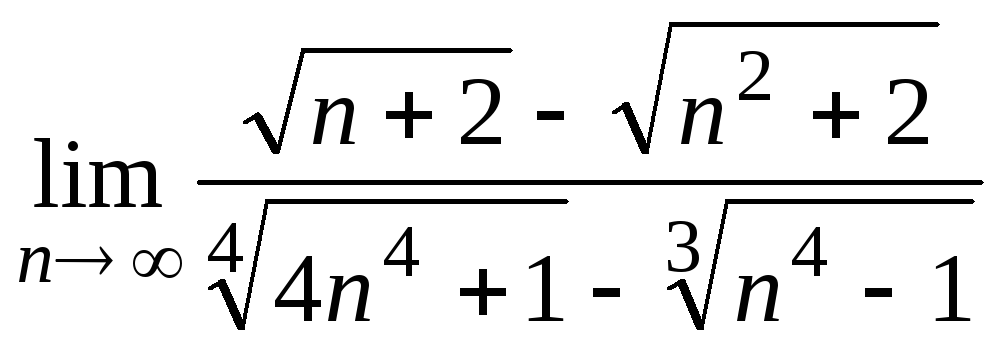 ;
4)
;
4)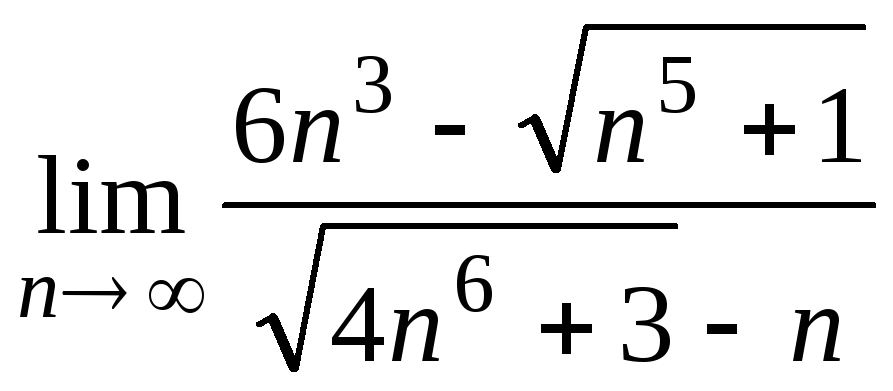 ;
;
5)
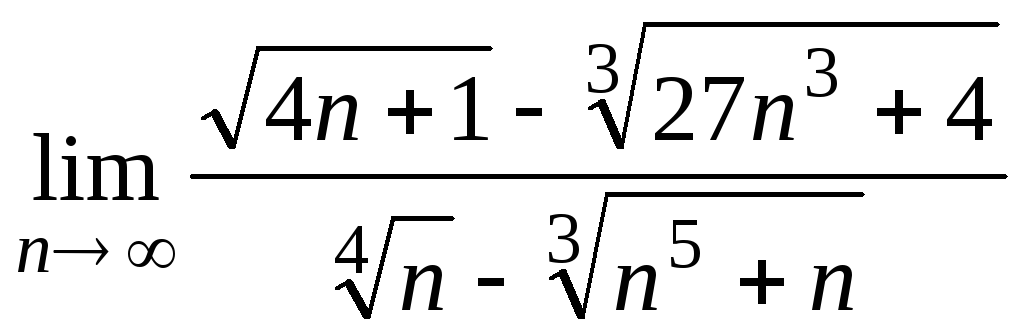 ;
6)
;
6)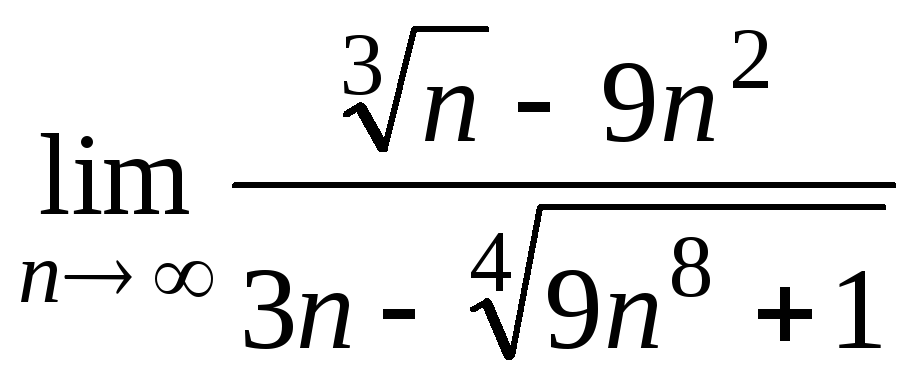 ;
;
7)
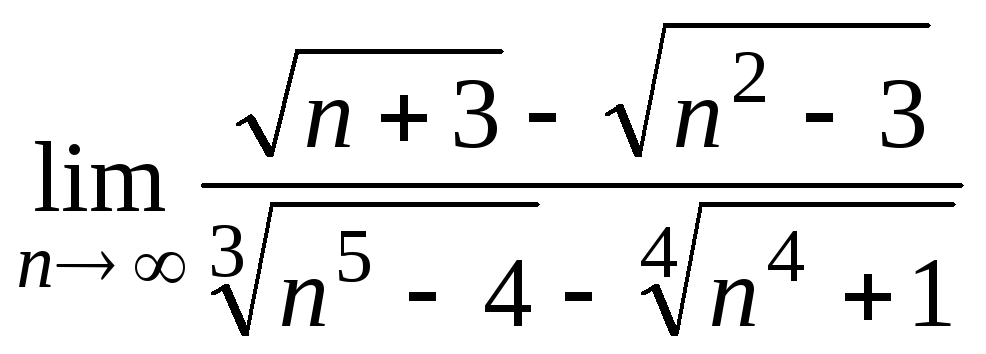 ;
8)
;
8)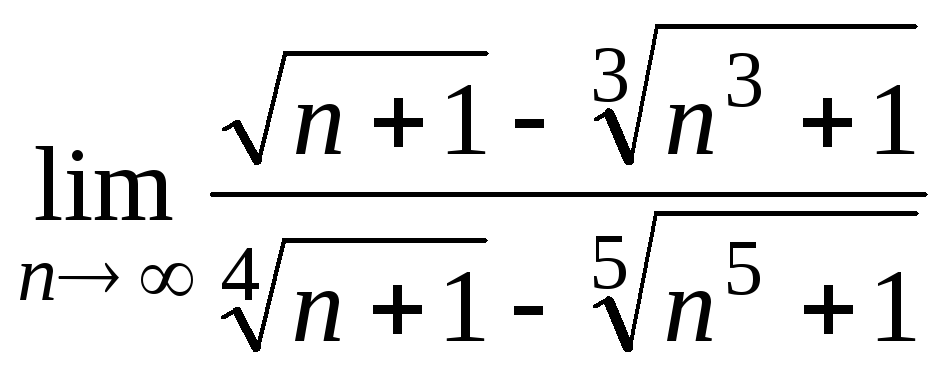 4
4
9)
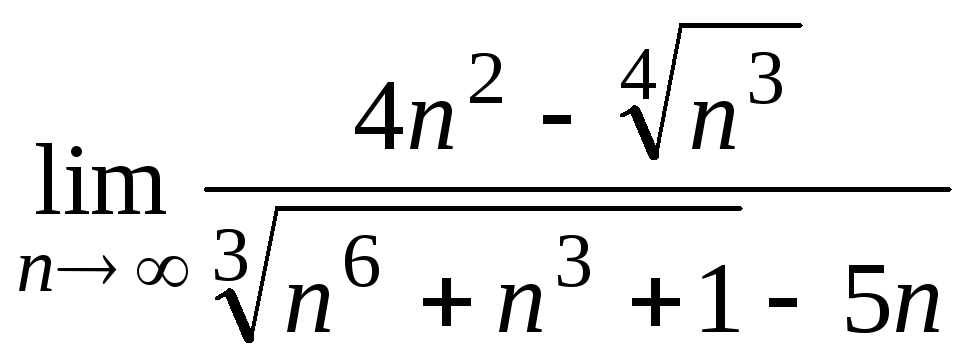 ;
10)
;
10)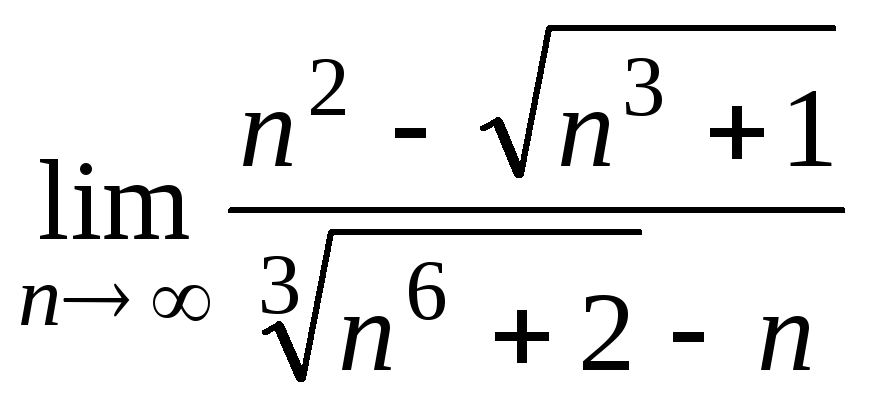 .
.
8


 ;
2)
;
2) ;
;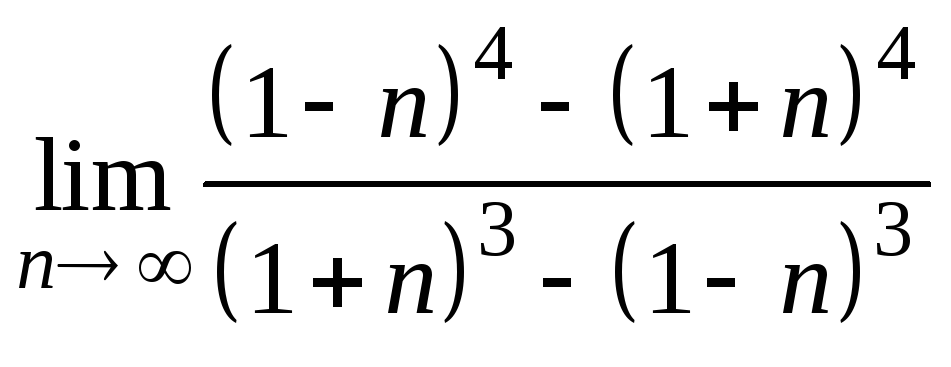 ;
4)
;
4)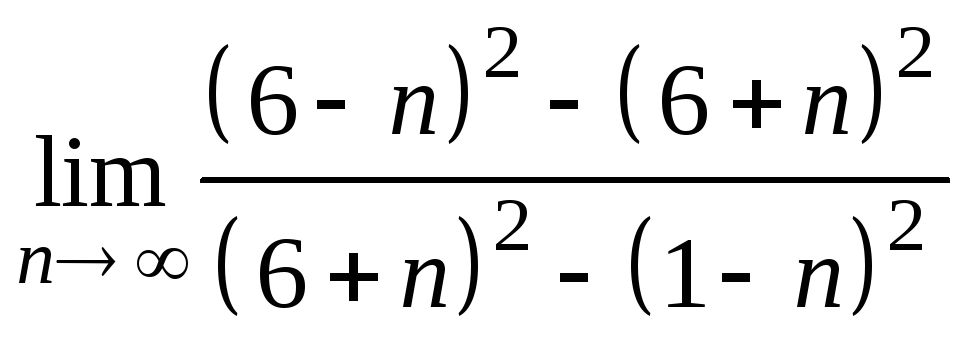 ;
;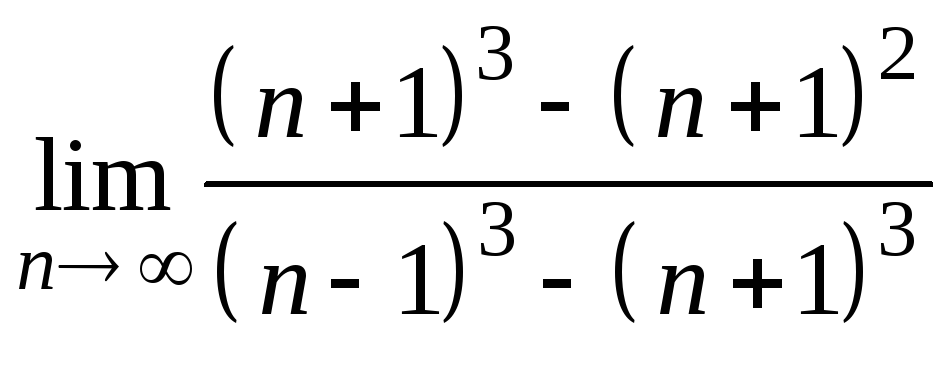 ;
6)
;
6)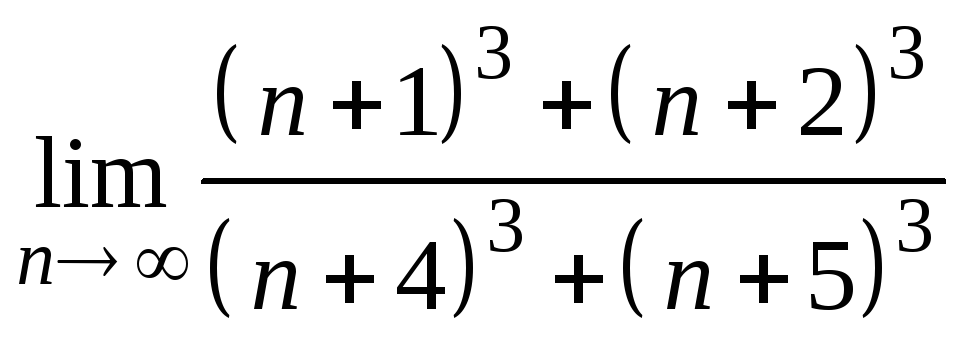 ;
;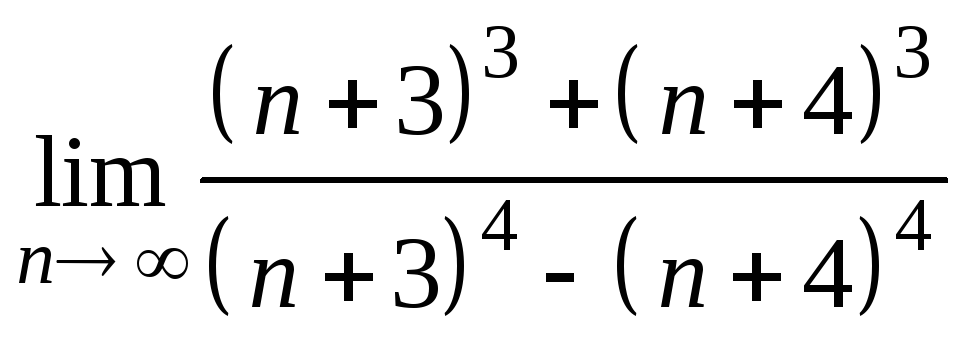 ;
8)
;
8) ;
;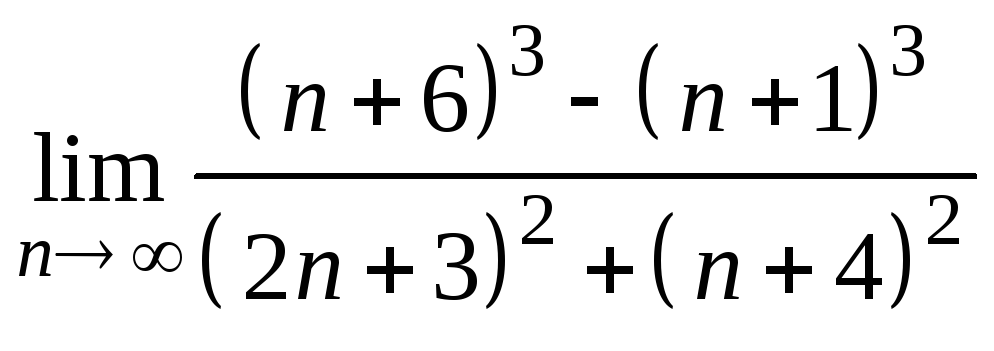 ;
10)
;
10)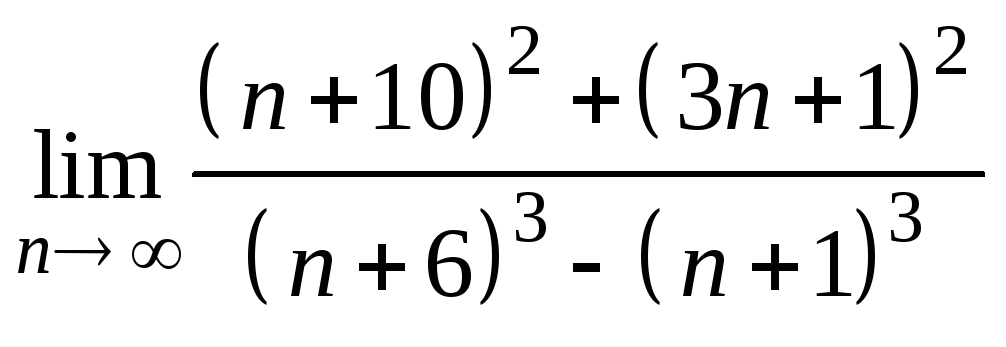 .
.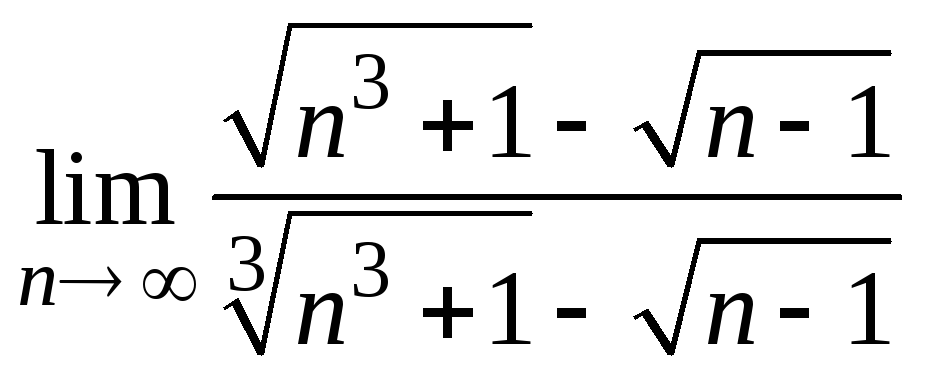 ;
2)
;
2)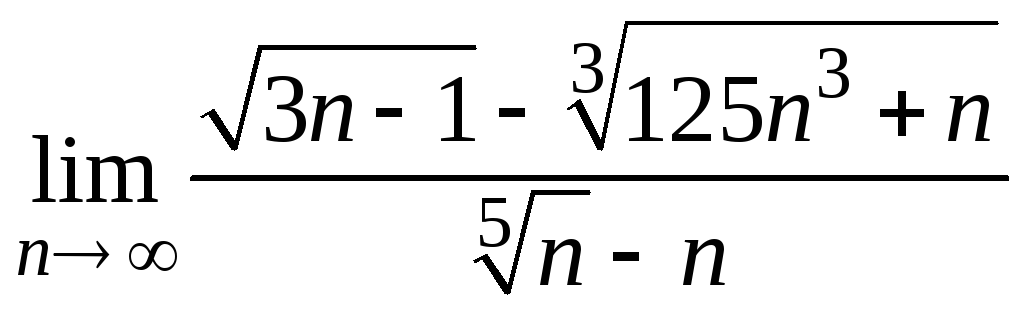 ;
;