лекция №4 анал

Лекция №4

1.10. Ограниченные числовые множества. Точные грани числовых множеств

Определение 1. Числовое множество называется ограниченным сверху (снизу), если существует число () такое, что для всех выполняется неравенство ().

Определение 2. Числовое множество, которое ограничено и сверху и снизу, называется ограниченным. Примерами ограниченных числовых множеств являются отрезок, интервал, полуоткрытый промежуток.

Число () называется верхней (нижней) границей множества .

Определение 3. Наименьшая из верхних границ непустого ограниченного сверху множества называется точной верхней гранью этого множества и обозначается (supremum).

Теорема 1. Непустое множество, ограниченное сверху, имеет точную верхнюю грань, притом единственную.

Теорема 2. Для того чтобы число было точной верхней гранью непустого числового множества , необходимо и достаточно, чтобы:

1) для всех выполнялось неравенство ;

2) для любого действительного числа нашлось такое , что .

Определение 4. Наибольшая из нижних границ непустого ограниченного снизу множества называется точной нижней гранью этого множества и обозначается (infimum).

Теорема 3. Непустое множество, ограниченное снизу, имеет точную нижнюю грань, притом единственную.

Теорема 4. Для того чтобы число было точной нижней гранью непустого числового множества , необходимо и достаточно, чтобы:

1) для всех выполнялось неравенство ;

2) для любого действительного числа нашлось такое , что .

Пример 1. Пусть , и , тогда

и .

Этот пример показывает, в частности, что нижняя и верхняя грани могут как принадлежать, так и не принадлежать самому множеству.

Пример 2. Пусть . Докажем, что , .

Решение. Для любого натурального числа имеем , а потому 1 – одна из верхних граней для . Предположим теперь, что . Тогда найдется такое , что . С другой стороны, , а потому при имеем . Из этого неравенства следует, что . Мы нашли, таким образом, элемент , такой, что . Итак, для множества и числа 1 выполнены оба сформулированных выше утверждения, и потому . Само число 1 не принадлежит .

Далее, имеем . Отсюда видно, что при увеличении разность увеличивается. Значит, наименьшее значение разности достигается при , и это значение равно . Таким образом, – наименьший элемент множества , а потому .

1.11.Лемма о вложенных отрезках

В математическом анализе при доказательстве многих важных утверждений аксиома полноты множества действительных чисел используется в виде принципа Коши-Кантора, называемого леммой о вложенных отрезках.

Определение 3. Система числовых отрезков

, , …, , …, , ,

называется системой вложенных отрезков, если

,

т.е., если

(рис. 1).

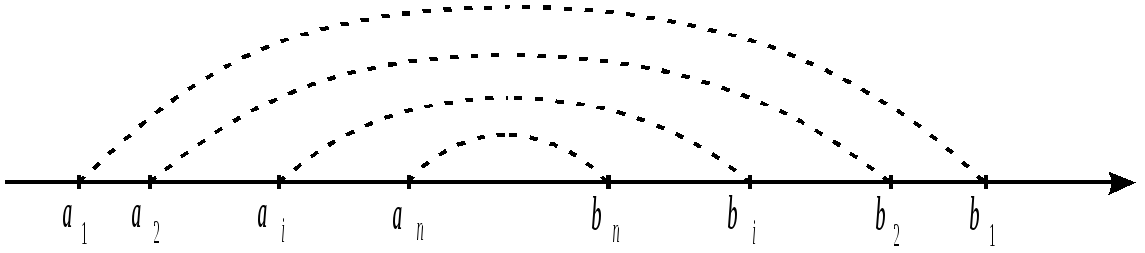
Рис. 1

Лемма 1. Всякая система вложенных числовых отрезков имеет непустое пересечение.

Доказательство. Для любых двух отрезков и нашей последовательности имеет место , в противном случае отрезки бы не имели бы общих точек. Таким образом для числовых множеств и выполнены условия аксиомы полноты, в силу которой найдется числотакое, что для любых и выполнено . В частности, для любого . А это и означает, что точка с принадлежит всем отрезкам.

Лемма 2. Для всякой системы вложенных отрезков, длины которых стремятся к нулю, существует единственная точка , принадлежащая всем отрезкам данной системы.

Существование такой точки следует из теоремы 1. Докажем единственность. Предположим противное. Пусть – две точки, обладающие этим свойством. Если они различны и, например , то при любом имеем , поэтому и длина каждого отрезка нашей последовательности не может быть меньше положительной величины . Значит, если в последовательности есть отрезки сколь угодно малой длины, то общая точка у них единственная

1.12. Классификация точек множества.

Определение 1. Для любого -окрестностью точки называется множество

.

В случае , а в случае .

Определение 2. Проколотой -окрестностью точки называется множество, получающееся удалением точки из ее -окрестности:

.

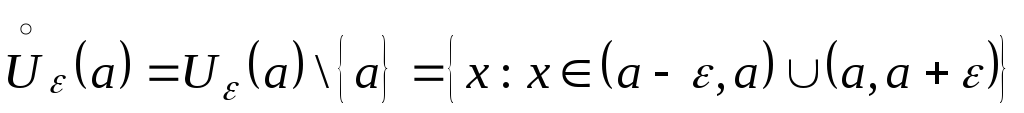Определение 3. Точка называется внутренней точкой множества , если существует -окрестность , целиком принадлежащая .

Определение 4. Точка называется граничной точкой множества , если в каждой ее окрестности существуют точки как принадлежащие множеству , так и не принадлежащие множеству .

Определение 5. Точка называется точкой прикосновения множества , если в каждой ее окрестности существует хотя бы одна точка, принадлежащая множеству .

Если точка прикосновения является одной из бесконечностей: , или , то она называется бесконечно удаленной точкой прикосновения.

Очевидно, что все элементы числового множества являются его точками прикосновения. Точками самого множества не исчерпываются, вообще говоря, все его точки прикосновения: могут существовать точки прикосновения и не принадлежащие ему. Например, точки и являются точками прикосновения интервала и не содержатся в нем.

Определение 6. Точка называется предельной точкой множества , если в каждой ее проколотой окрестности существует хотя бы одна точка, принадлежащая множеству .

Предельная точка всегда является точкой прикосновения, но не наоборот. Для множества рациональных чисел предельной является каждая точка R, так как в любом интервале вещественных чисел имеются рациональные числа.

Определение 7. Точка называется изолированной точкой множества , если у нее существует окрестность, не содержащая других точек множества , кроме самой точки .

Пример. Рассмотрим множество . Для этого множества:

0, 1, 5 – граничные точки;

и – точки прикосновения;

– предельные точки;

5 – изолированная точка.

1.13. Открытые и замкнутые множества. Теорема Больцано-Вейерштрасса

Определение 8. Множество, содержащее все свои предельные точки, называется замкнутым.

Определение 9. Множество, у которого все точки являются внутренними, называется открытым.

Определение 10. Совокупность всех точек прикосновения множества называется его замыканием .

Определение 11. Ограниченное замкнутое множество называется компактом.

Теорема (Больцано-Вейерштрасса). Всякое бесконечное ограниченное числовое множество имеет хотя бы одну предельную точку.

Доказательство. Пусть А – ограниченное множество, тогда существует такой отрезок [c, d], которому принадлежит А. Так как А – бесконечное множество, то хотя бы на одной из двух половин [c, (c+d)/2], [(c+d)/2, d] отрезка [c, d] имеется бесконечное подмножество множества А. Пользуясь этим очевидным предположением, отправляясь от отрезка [c, d] =∆₁ с заданным на нем бесконечным множеством точек А, построим систему вложенных отрезков ∆_n, где каждый последующий отрезок составляет половину предыдущего и несет на себе бесконечное подмножество множества А. По принципу Кантора у этой системы есть общая точка х₀, докажем, что она является предельной для множества А. Возьмём любой интервал V с центром в точке х₀ ,скажем, длины σ>0. Пусть n таково, что длины отрезка ∆_n меньше σ/2. Включая в себя точку х₀, он целиком содержится в интервале V. Вместе с отрезком ∆_n в интервал V попадет бесконечное число точек множества А. Следовательно, х₀ есть предельная точка множества А, что и требовалось доказать.

Эта теорема также выражает принцип полноты числовой прямой, как и леммы Коши-Кантора и Бореля-Лебега.

Лемма Бореля-Лебега

Лемма (Бореля-Лебега). Всякое открытое множество на числовой оси представляет собой сумму конечного или счетного числа попарно непересекающихся интервалов.

Теорема 1. Объединение конечного числа и пересечение произвольного числа замкнутых множеств есть замкнутое множество.

Теорема 2. Дополнение замкнутого множества есть множество открытое.

Теорема 3. Объединение произвольного числа и пересечение конечного числа открытых множеств есть открытое множество.

Перечислим также некоторые следствия, вытекающие из рассмотренных выше определений и утверждений.

1) Конечное множество не имеет предельных точек.

2) Каждое рациональное число является точкой прикосновения множества иррациональных чисел.

3) Каждое действительное число является точкой прикосновения множества рациональных чисел.

4) Пустое множество замкнуто и открыто одновременно.

5) Множество не открыто и не замкнуто в .

6) Множество является как открытым, так и замкнутым.

7) Любая -окрестность точки – открытое множество.

8) Отрезок является замкнутым множеством.

4