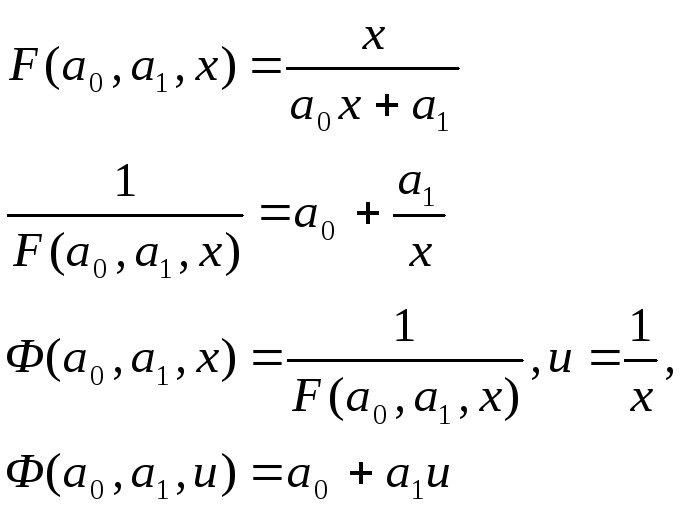1.2 Квадратичная модель

Пусть . Тогда ,,и система (1) будет иметь вид:

(4)

Отсюда получаем систему трех уравнений с тремя неизвестными.

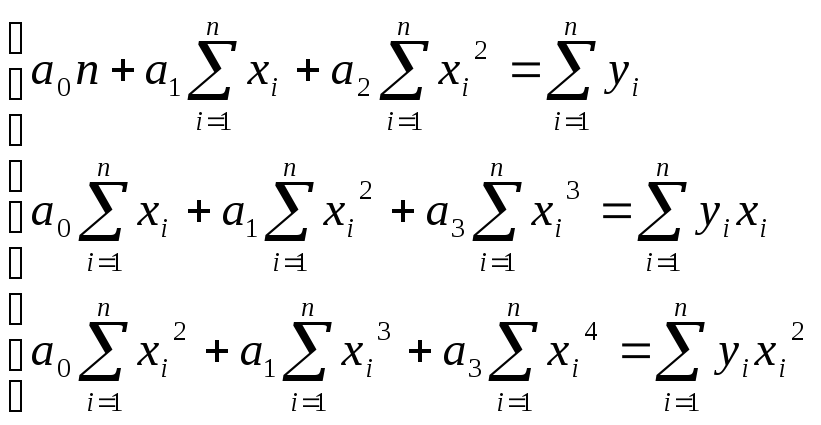(5)

Реализация в пакете Mathcad:

{ В данном примере, как и в предыдущем, приводится отладочный вариант программы. При практическом применении программы f(x) не используется, а в качестве X и Y вводятся экспериментальные значения.}

ORIGIN:=1

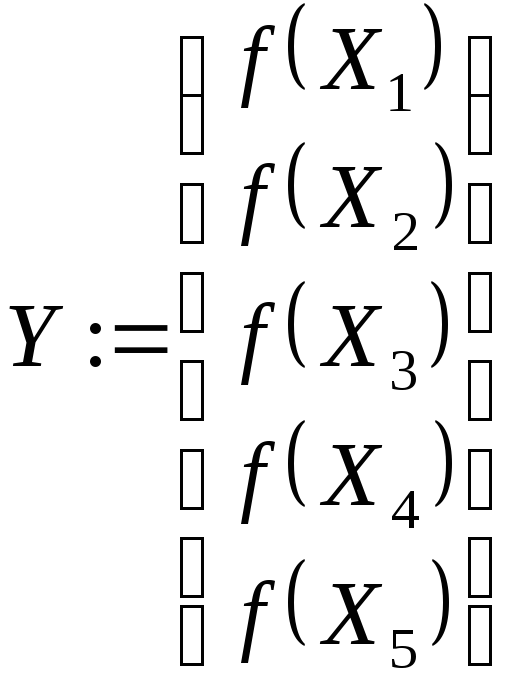
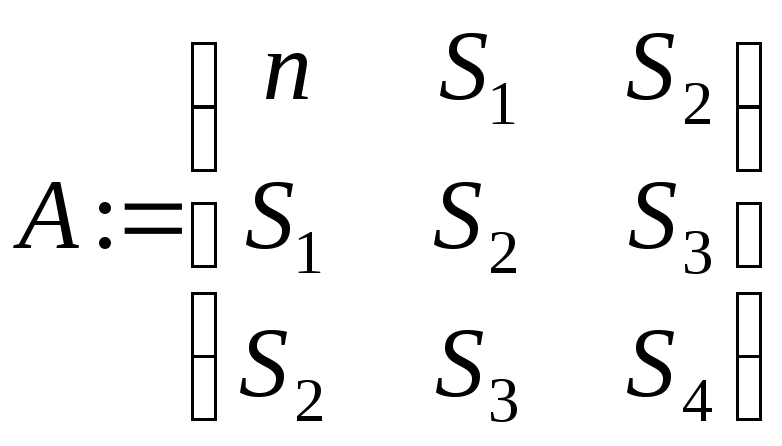
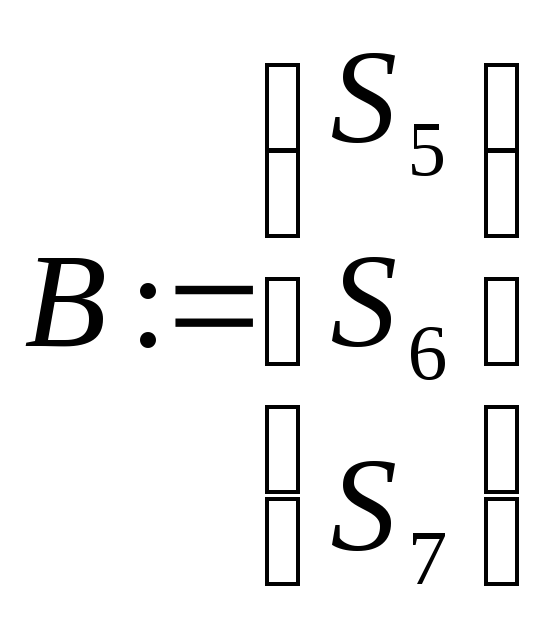
Пример 2

Для функции, заданной таблицей

х у

0.2 -1

1.2 -0.5

2.3 -0.6

3.7 0.2

4.3 1.3

построить квадратичную аппроксимацию методом наименьших квадратов.

При решении этой задачи в приведенной выше программе в качестве Х и У вводятся заданные табличные значения. Аппроксимирующее квадратичное приближение имеет вид График приближающей функции и исходные точки изображены на рисунке 2:

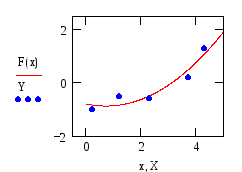
Рисунок 2

1.3 Пусть . Тогда ,, … ,

После преобразований система (1) примет вид:

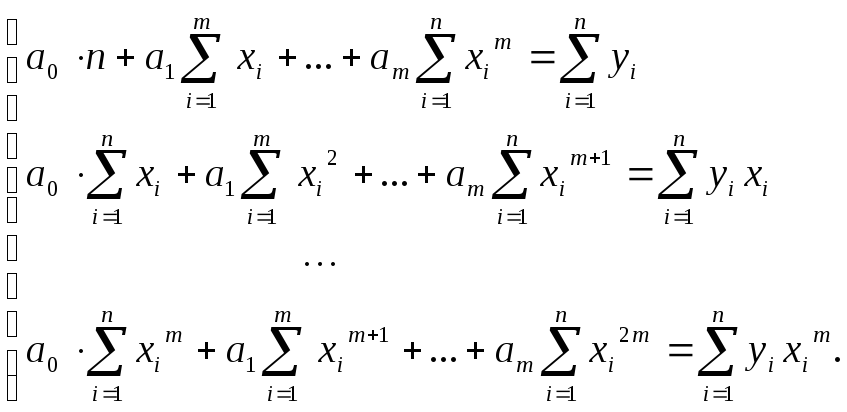(6)

При условии определитель матрицы коэффициентов системы отличен от нуля и система имеет единственное решение. Решив ее, получим коэффициенты аппроксимирующего многочлена.

1.4 В ряде случаев аппроксимирующую функцию ищут не в виде полинома, а в форме некоторой функции специального вида.

а) приближение показательной функцией:

(7)

Если применить метод наименьших квадратов непосредственно, то получим систему нелинейных уравнений, решить которую весьма затруднительно. Поэтому, сначала произведем замену переменных таким образом, чтобы линеаризовать функцию .В частности, для показательной функции можно применить логарифмирование при условии :. Т.к., функция F является приближающей для функции f, функция будет приближающей для . После замены переменных

, (8)

получим линейную форму (9)

т.е., задача свелась к отысканию приближающей функции в виде линейной.

Практически для нахождения приближающей функции в виде показательной необходимо проделать следующее:

-по данной таблице составить новую, прологарифмировав значения у в исходной таблице;

-по новой таблице найти параметры приближающей функции вида (9);

-используя (8), найти значения параметров по формулами подставить их в выражение (7).

Реализация в пакете Mathcad:

ORIGIN: =1

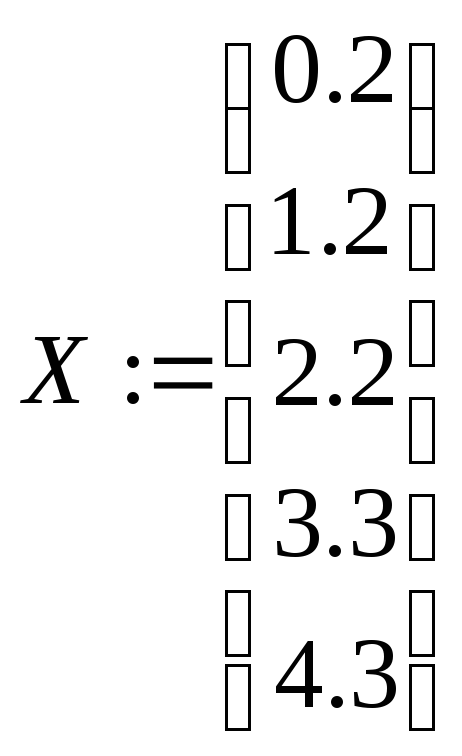
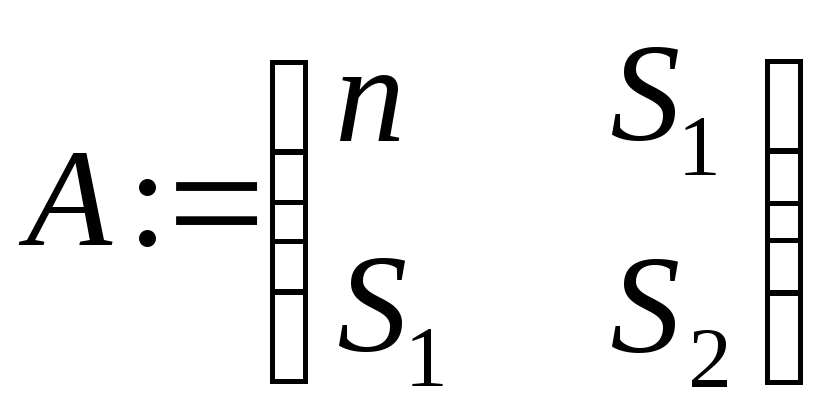
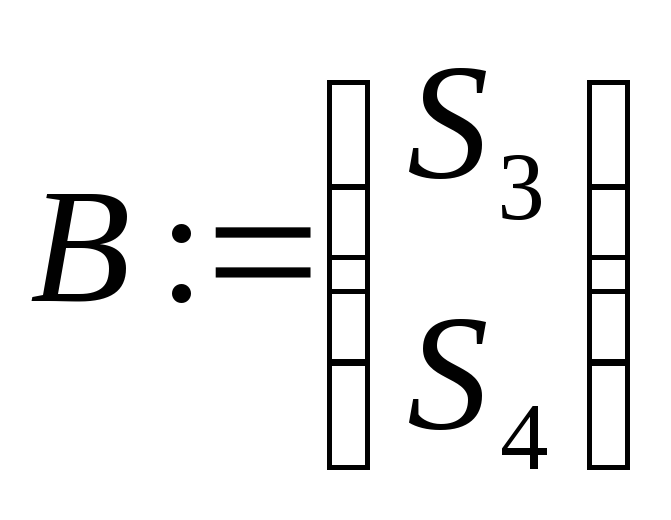
{ Т.е. получили функцию }

В данном примере, как и в предыдущих, приведен отладочный вариант программы. При практическом использовании в качестве X и Y требуется ввести экспериментальные значения.

Пример 3

Для функции, заданной таблицей

х у

0.2 1

1.2 0.5

2.3 -0.6

3.7 0.2

4.3 1.3

построить показательную аппроксимацию методом наименьших квадратов.

При решении этой задачи в приведенной выше программе в качестве Х и У вводятся заданные табличные значения. Аппроксимирующее квадратичное приближение имеет вид График приближающей функции и исходные точки изображены на рисунке 3:

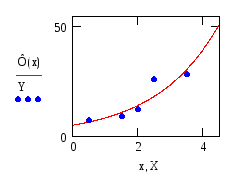
Рисунок 3

б)Степенная функция.

Будем искать приближающую функцию в виде (10)

Предполагая, что в исходной таблице значения аргумента и значения функции положительны, прологарифмируем равенство (10):

(11)

Т.к., функция F является приближающей для функции , функциябудет приближающей для.

Введем новую переменную .

Тогда, будет функцией от.

Обозначим (12)

Теперь равенство (11) принимает вид

(13)

т.е., снова, задача свелась к отысканию приближающей функции в виде линейной.

Практически для нахождения приближающей функции в виде степенной необходимо проделать следующее:

по данной таблице составить новую таблицу, прологарифмировав значения х и у в исходной таблице

по новой таблице найти параметры приближающей функции вида (13)

используя обозначения (12), найти значения параметров и подставить их в выражение (10)

в)Дробно-линейная функция

Будем искать приближающую функцию в виде

(17)

Обозначим :

,

Таким образом, по заданной таблице нужно составить новую таблицу, у которой значения аргумента оставить прежним, а значение функции заменить обратными числами, после чего для полученной таблицы найти приближенную функцию вида . Найденные значения параметровподставить в (17).

г) Логарифмическая функция

(18)

Подстановка приводит к линейной функции

д) Гипербола

Подстановка , приводит к линейной функции:

е) Дробно-рациональная функция