
g3
.pdf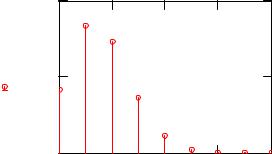
ГЛАВА 3. СТАНДАРТНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
§1. Биномиальное распределение
Пусть эксперимент проводится по схеме Бернулли.
Определение. Дискретная случайная величина ξ имеет биномиальное распределение с параметрами n, p , если вероятности отдельных ее возможных значений определяются формулой Бернулли:
P(ξ = m)≡ P(m, p)= Cmn pm (1 − p)n−m, m = 0,1,...n, n =1,2,...., 0 ≤ p ≤1
Случайная величина, имеющая биномиальное распределение с параметрами n, p , представляет собой число наступлений события А в n независимых испытаниях, в каждом из которых вероятность наступления этого события равняется p .
График биномиального распределения вероятностей представлен на Рис. 1.
0.4
P(m,p)0.2
00 |
2 |
4 |
6 |
8 |
|
|
m |
|
|
Рис. 1. Биномиальное распределение P(m, p) при n = 8 и p = 0.2 . |
||||
Найдем основные числовые характеристики биномиального распределения. Для этого сначала введем обозначения. Пусть ξ – (СВ) числа появлений события А в n независимых испытаниях, 0,1, … n – ее возможные
n
значения. Тогда ξ можно представить в виде ξ = ∑ξi , где ξi – (СВ) числа i=1
появлений события А в i-ом испытании, которая принимает значения либо 0, либо 1 с вероятностями равными (1 − p) и p соответственно. Следовательно,
M (ξi )= p, D(ξi )= p(1 − p),
так что по свойству математического ожидания
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
M (ξ)= M ∑ξi |
= |
∑M |
(ξi )= np . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично, дисперсия биномиального распределения равна |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
D(ξ)= D ∑ξi = |
∑D(ξi )= np(1 − p), σ(ξ)= np(1 − p). |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i=1 i=1 |
|
|
|
|
|
|
|
μ3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Найдем |
коэффициент асимметрии |
A |
|
= |
|
и коэффициент |
эксцесса |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
μ4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
σ3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Ek = |
−3 . Для этого найдем соответствующие центральные моменты |
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
σ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
μ |
2 |
=ν |
2 |
−ν 2 |
= D(ξ), μ |
3 |
=ν |
3 |
−3ν ν |
+ 2ν |
3, μ |
4 |
=ν |
4 |
|
− 4ν ν |
+ 6ν |
2ν |
2 |
−3ν 4 . |
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 2 |
|
|
1 |
|
|
|
|
1 3 |
|
|
1 |
|
|
1 |
||||||||||||||
Так как |
по |
|
определению |
начальный |
момент |
второго |
|
порядка равен |
||||||||||||||||||||||||||||||
ν2 = ∑m2P(m, p) и ν2 = D(ξ)+ M 2 (ξ)= np(1 − p)+ (np)2 , то, с одной стороны, |
||||||||||||||||||||||||||||||||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
∂ν |
2 |
|
|
|
m |
|
(n |
− m) |
|
|
|
|
|
ν |
|
|
nν |
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
= |
∑m |
2 |
− |
|
|
|
|
P(m, p)= |
|
3 |
− |
|
|
|
, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
q |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂p |
|
|
m |
p |
|
|
|
|
|
|
|
|
|
|
pq |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а, с другой стороны,
∂∂νp2 = n(q − p)+ 2 pn2 ,
откуда следует ν3 = npq(q − p)+3q(np)2 + (np)3 . С учетом полученных соотношений для центрального момента третьего порядка получим
μ3 = npq(q − p), q ≡1 − p ,
так что коэффициент асимметрии равен
A = |
|
μ3 |
|
= |
(q − p). |
|||
|
|
|||||||
s |
σ3 |
|
|
npq |
||||
Аналогично, коэффициент эксцесса |
|
|
|
|
|
|||
Ek = |
μ4 |
−3 |
= |
1 − 6 pq |
. |
|||
|
|
|||||||
|
σ 4 |
|
|
|
npq |
|||
Мода биномиального распределения определяется выражением

Mo = trunc[(n +1)p],
где функция trunc[(n +1)p] обозначает целую часть числа [(n +1)p]. Если число [(n +1)p] – целое, то распределение имеет два модальных значения [(n +1)p] и [(n +1)p]-1.
Медиана биномиального распределения равна
Me = np ,
если np – целое число. Если же np – дробное число, то медиана равна одному из двух целых чисел trunc[np]±1, ближе всего расположенных к np .
Из Рис. 1. видно, что последовательность вероятностей P(m, p) сначала
монотонно возрастает с |
увеличением |
m |
– до |
достижения |
моды |
Mo = trunc[(n +1)p]= trunc[1.6]=1 |
(или двух |
модальных |
значений), а |
затем |
|
начинает монотонно падать.
Определение. Дискретная случайная величина ξ имеет геометрическое распределение, если вероятности отдельных ее возможных значений определяются формулой:
P(m)= qm−1p,
где ξ – (СВ) числа испытаний, проводимых до первого появления события А; p – вероятность появления события А в каждом отдельном испытании, q =1− p ; m – число испытаний, проводимых до первого появления события А. Геометрическое распределение имеет следующие числовые характеристики:
M (ξ)= 1 , D(ξ)= q .
p p2
Таким образом, математические испытания геометрического распределения удовлетворяют правилу пропорциональности: для получения события А
дважды в среднем потребуется в 1p раз больше испытаний, чем для
получения одного события.
Определение. Дискретная случайная величина ξ имеет гипергеометрическое распределение, если вероятности отдельных ее возможных значений определяются формулой:
|
Cm Cn−m |
|
P(m)= |
M N −M |
, |
|
||
|
Cn |
|
|
N |
|
где N – общее число элементов некоторого множества А, M – число элементов подмножества А, обладающих некоторым свойством; испытание состоит в отборе наугад n элементов, среди которых m обладают указанным свойством; ξ – (СВ) числа наугад выбранных элементов, обладающих указанным свойством.
Гипергеометрическое распределение имеет следующие числовые характеристики:
M (ξ)= nM |
, D(ξ)= nM (N − M )(N −n). |
N |
N 2(N −1) |
Определение. Дискретная случайная величина ξ имеет полимодальное
распределение, если вероятности отдельных ее возможных значений определяются формулой:
P(X |
, X |
2 |
, X |
3 |
...X |
k |
)= |
|
n! |
|
|
p X1 p X 2 |
... p X k , |
|
X ! X |
|
!...X |
|
|
||||||||||
1 |
|
|
|
|
2 |
k |
! 1 2 |
k |
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
где X1– число элементов, обладающих свойством А, |
X2 – число элементов, |
|||||||||||||
обладающих свойством В, … X k – число элементов, обладающих свойством
С; A + B +....+C = n – общее число элементов; p1– |
вероятность выбора |
||
элемента, обладающего свойством А, |
p2 – вероятность выбора |
элемента, |
|
обладающего свойством В, … pk – |
вероятность |
выбора |
элемента, |
обладающего свойство С; испытание состоит в отборе n элементов, среди которых X1 обладают свойством А, X2 – свойством В, …. X k – свойством С;
ξ – (СВ) числа наугад выбранных элементов, обладающих указанными свойствами.
§2. Распределение Пуассона
Определение. Дискретная случайная величина ξ имеет распределение Пуассона с параметром λ , если вероятности отдельных ее возможных значений определяются формулой:
P(ξ = m)≡ P(m, λ)= λm exp(− λ), m!
m = 0,1,...∞, λ > 0
График распределения Пуассона представлен на Рис. 2.

0.8
0.6 
P(m,λ)0.4
0.2
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
2 |
|
4 |
|
|
|
6 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. Распределение Пуассона P(m, λ) |
при λ = 0.5 . |
|
|||||||||||||||||||||||||
|
Найдем основные числовые характеристики распределения Пуассона. |
|||||||||||||||||||||||||||||
Разложим экспоненту eλ в ряд Маклорена eλ |
|
∞ |
|
λm |
|
∞ |
λm−1 |
|
|
|||||||||||||||||||||
= ∑ |
|
= ∑ |
. Тогда |
|||||||||||||||||||||||||||
|
|
m! |
(m −1)! |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m=0 |
m=1 |
|
||||||||||
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λm−1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
M (ξ)= ∑mP(m, λ)= λe−λ ∑ |
|
|
= λe−λeλ |
= λ . |
|
||||||||||||||||||||
|
|
|
|
|
(m −1)! |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
m=0 |
|
|
|
|
|
|
m=1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично, для среднего квадрата получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
∞ |
2 |
P(m, λ)= |
|
−λ |
∞ |
λm−1 |
|
|
−λ |
|
(1 + λ)e |
λ |
|
2 |
|
|
|||||||||
|
M ξ |
|
= ∑m |
|
λe |
|
|
|
∑ m |
|
|
|
= λe |
|
|
|
|
= λ + λ , |
||||||||||||
|
|
|
|
(m −1)! |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
m=0 |
|
|
|
|
|
|
m=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
так что дисперсия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
D(ξ) |
|
|
ξ |
2 |
2 |
|
= λ . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= M |
− (M (ξ)) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Остальные числовые характеристики распределения Пуассона |
|||||||||||||||||||||||||||||
следующие: |
коэффициент асимметрии A = μ3 = 1 |
, |
коэффициент эксцесса |
|||||||||||||||||||||||||||
|
μ4 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
s |
σ3 |
|
|
|
λ |
|
|
|
|
|
|
||||
Ek = |
−3 = |
. Если λ – дробное число, то мода Mo = trunc[λ], а если число λ |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
σ 4 |
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
– целое число, то распределение Пуассона имеет два модальных значения λ и λ −1. Медиана распределения Пуассона равна Me = λ , если λ – целое число. Если же λ – дробное число, то медиана равна одному из двух целых чисел trunc[λ]±1, ближе всего расположенных к λ .
Отметим, что последовательность вероятностей P(m, p) сначала монотонно возрастает с увеличением m – до достижения моды (или двух модальных значений), а затем начинает монотонно убывать.
§3. Закон равномерного распределения
Определение. Распределение непрерывной (СВ) называют равномерным, если на интервале, содержащем возможные значения непрерывной (СВ), плотность распределения является константой, т.е.
0, |
x ≤ a |
|
f (x)= A, |
a < x ≤ b |
(1) |
|
x > b |
|
0, |
|
В точках x = a, x = b плотность |
f (x) |
– терпит разрыв. Константу А найдем из |
|||||||||||||||
условия нормировки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∞ |
|
|
|
|
b |
|
|
|
|
|
|
|||
|
|
|
∫ f |
(x)dx = A∫dx = A(b − a)=1, |
|
||||||||||||
|
1 |
|
−∞ |
|
|
|
|
a |
|
|
|
|
|
|
|||
так что A = |
. Для нахождения функции распределения воспользуемся |
||||||||||||||||
b − a |
|||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
свойством F(x)= |
∫ f (x)dx . При этом получим: |
|
|||||||||||||||
|
|
−∞ |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) при (−∞ < x ≤ a) |
F(x)= |
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫0dx = 0 ; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
a |
|
|
|
1 |
|
|
x |
|
x − a |
|
|
|||
2) при (a < x ≤ b) F(x)= ∫0dx + |
|
|
|
∫dx = |
; |
|
|||||||||||
b − a |
|
|
|||||||||||||||
|
|
|
−∞ |
|
|
a |
|
b − a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) при (x > b) |
F(x) |
a |
|
|
1 |
|
b |
|
|
|
x |
|
|
|
|
||
= ∫0dx + |
|
|
∫dx + ∫0dx =1; |
|
|||||||||||||
b |
− a |
|
|||||||||||||||
|
|
|
−∞ |
|
a |
|
|
|
b |
|
|
|
|
||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0, |
x ≤ a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
− a |
|
|
|
|
||
|
|
|
|
|
F(x) |
= |
x |
, a < x ≤ b |
(2) |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
b − a |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1, |
x > b |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда видно, что функция распределения F(x) всюду непрерывна. Определим числовые характеристики равномерного распределения.
С учетом (1) математическое ожидание и дисперсия равны:
∞ |
1 |
b |
|
|
|
M (ξ)= ∫xf (x)dx = |
∫xdx = a +b |
, |
|||
b − a |
|||||
−∞ |
a |
2 |
|
||
|
|
|
|||

∞ |
2 |
|
1 |
b |
2 |
|
(b − a)2 |
|
b − a |
|
||
D(ξ)= ∫ |
(x − M (ξ)) |
f (x)dx = |
|
∫ |
(x − M (ξ)) |
dx = |
|
, σ(ξ)= |
|
|
. |
|
b − a |
12 |
2 |
3 |
|||||||||
−∞ |
|
a |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
Если (α, β) (a, b), то по свойству функции распределения (2)
P(α ≤ ξ < β)= F(β)− F(α)= βb −−αa .
Пример. Жеглов и Фокс условились встретиться в ресторане между 0 и 2 часами. Пришедший первым Жеглов ждет Фокса в течение 10 минут, после чего уходит, а Фокс ждет 20 мин. Чему равна вероятность встречи этих лиц, если моменты прихода каждого из них независимы и распределены равномерно в интервале (0,2).
Решение. Пусть ξ – (СВ) времени прихода Жеглова, x – возможные значения ξ ; η – (СВ) времени прихода Жеглова, y – возможные значения η . По задачи плотность вероятности системы (СВ) {ξ,η}равна
f |
ξη |
(x, y)= f |
ξ |
(x)f |
(y)= |
|
1 |
= |
1 |
. |
|
|
|
||||||||
|
|
η |
(2 |
− 0)2 |
4 |
|
||||
|
|
|
|
|
|
|
||||
Тогда
P[(ξ,η) D]= |
1 |
∫∫dxdy, |
(1) |
|
4 |
D |
|
|
|
|
где по условию задачи область интегрирования ограничена следующими линиями:
|
|
|
|
|
1 |
|
|
|
|
|
x = 2, y = 2, y = x + |
6 . |
|
|
(2) |
||
|
D : |
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
x = 0, y = 0, y = x − |
3 |
|
|
|
||
Учитывая (2), из (1) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
P[(ξ,η) D]= |
∫∫dxdy = |
∫∫dxdy + ∫∫dxdy + ∫∫dxdy , |
(3) |
|||||
|
4 |
D |
4 |
|
D2 |
D3 |
|
|
|
|
|
D1 |
|
|
|||
здесь

|
|
1 |
, |
y = x + |
1 |
|
x = 11 , y = x |
+ 1 |
|||
D |
x = |
3 |
6 |
, D |
|
6 |
|
6 |
|||
: |
|
|
: |
|
|||||||
1 |
|
|
|
|
|
2 |
|
1 |
, y = x − |
1 |
. |
|
x = 0, y = 0. |
|
|
x = |
3 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
||
,x = 2, y = 2,
,D3 : x = 11 , y = x − 1 . (4)
6 3
С учетом (4) из (3) окончательно найдем
P[(ξ,η) D]= |
1 |
1/ 3 x+1/ 6 11/ 6 x+1/ 6 |
2 |
2 |
67 |
|
||||
∫ dx ∫dy + ∫ dx ∫dy + ∫ dx ∫dy |
= |
. |
||||||||
4 |
288 |
|||||||||
|
0 |
0 |
1/ 3 x−1/ 3 |
11/ 6 |
x−1/ 3 |
|
|
|||
§4. Интеграл Эйлера-Пуассона
Интегралом Эйлера-Пуассона называют несобственный интеграл вида
I ≡ ∞∫e−x2 dx = 2∞∫e−x2 dx .
−∞ 0
Этот интеграл часто будет встречаться в дальнейшем. Вычислим его способом Пуассона. Для этого рассмотрим двойной интеграл
∞∫∞∫e−(x2 +y2 )dxdy = I 2 . 4
0 0
Проведем вычисление этого интеграла в полярных координатах
x = ρ cos(ϕ)y = ρ sin(ϕ)
ρ2 = x2 + y2
Тогда
∞∞ |
−(x2 +y2 ) |
π / 2 ∞ |
−ρ2 |
|
π |
∞ |
−ρ2 |
|
π |
|
I |
2 |
|
|
∫ ∫e |
dxdy = |
∫ |
∫e |
|
ρdρdϕ = |
|
∫e |
|
ρdρ = |
|
= |
|
|
, |
|
2 |
|
4 |
4 |
||||||||||
0 0 |
|
0 |
0 |
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
откуда следует, что I =  π , что и требовалось получить.
π , что и требовалось получить.
|
|
§5. Нормальный закон распределения |
|
|
|
||||||||||||||
Среди всех законов распределения (СВ) наибольшее теоретическое и |
|||||||||||||||||||
практическое значение имеет нормальный закон распределения. Дело в том, |
|||||||||||||||||||
что согласно центральной предельной теореме он является предельным |
|||||||||||||||||||
законом, к которому приближаются другие законы распределения при весьма |
|||||||||||||||||||
часто встречающихся типичных условиях. |
|
|
|
|
|
|
|
||||||||||||
Определение. Распределение непрерывной (СВ) |
ξ называют нормальным |
||||||||||||||||||
(кратко |
|
2 |
если |
соответствующая |
ей |
плотность |
распределения |
||||||||||||
N a,σ |
), |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражается формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
= |
1 |
|
|
|
(x − a)2 |
|
− ∞ < x < ∞,σ > 0 , |
||||||
|
|
fξ x, a,σ |
|
|
σ |
2π |
|
exp− |
|
|
2 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
2σ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где a,σ – параметры распределения. |
|
Используя интегральную связь функции |
|||||||||||||||||
распределения с плотностью распределения, представим функцию |
|||||||||||||||||||
нормального распределения в удобном для табулирования виде |
|
||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x − a |
|
|
|
||
|
|
|
F(x) |
= ∫ fξ (x, a,σ )dx |
|
|
|
|
|||||||||||
|
|
|
= Φ1 |
σ |
, |
|
|
|
|||||||||||
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
−t2 |
|
|
|
|
|
|
|
|
||
где функция Лапласа Φ (z) |
|
|
1 |
z |
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
∫ |
e |
2 dt , для которой составлены таблицы. |
|||||||||||||||
|
|
|
1 |
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
−t2 |
|
Кроме того, составлены таблицы и для функции Φ0 (z)= |
21π |
z |
|||||||||||||||||
∫e |
2 dt . Между |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
этими функциями существует очевидное соотношение Φ1(x)= Φ0 (x)− 0.5 . |
|||||||||||||||||||
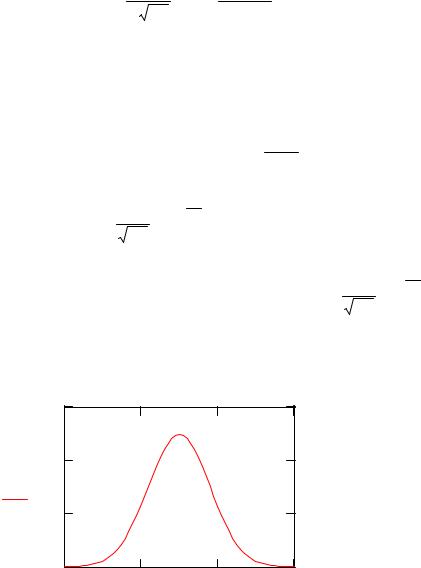
График нормального распределения представлен на Рис. 3. |
|||||||||||||||||||
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x,a,σ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
|
2 |
|
|
|
|
4 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Рис. 3. Нормальное распределение f (x,3,0.8). |
|
|
|||||||||||||||
Для выяснения вероятностного смысла параметров a,σ определим основные числовые характеристики (СВ), распределенной по нормальному закону. По свойству математического ожидания M (ξ)= a + M (ξ − a), где
∞
M (ξ − a)= ∫(x − a)f (x, a,σ)dx = 0 ,
−∞
так как подынтегральная функция четная, а пределы симметричные, так что
параметр |
|
|
a |
нормального распределения является математическим |
||||||||||||||||||||||||||||||
ожиданием M (ξ)= a , и, следовательно, |
Mo = Me = a . Аналогично, центральный |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
момент |
третьего |
|
порядка |
μ3 = |
∫(x − a)3 f (x, a,σ)dx = 0 , |
так |
что коэффициент |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
μ3 |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
асимметрии |
A |
= |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
s |
|
|
σ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя интеграл Эйлера-Пуассона, дисперсию вычислим |
||||||||||||||||||||||||||||||
непосредственно по определению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
D(ξ)= |
∞ |
|
|
|
2 |
f (x, a,σ )dx |
= |
|
1 |
|
|
∞ |
|
2 |
|
(x − a)2 |
|
|
t = x − a |
= |
||||||||||||||
∫ |
(x − a) |
|
|
|
|
∫ (x − a) |
|
exp |
− |
|
2σ |
2 |
dx = |
σ 2 |
||||||||||||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
σ 2π −∞ |
|
|
|
|
|
|
|
|
|
|
dx =σ 2dt |
||||||||
|
2σ |
2 |
∞ |
|
2 |
|
|
|
|
2 |
|
|
2σ |
2 |
|
2 |
|
−t2 |
∞ |
1 |
|
∞ |
|
|
|
2 |
|
|
|
2 |
|
|||
= |
|
∫ |
t |
|
−t |
|
|
−t |
e |
− |
|
|
|
−t |
|
=σ |
|
|||||||||||||||||
|
π |
|
exp |
|
dt = |
|
π |
|
|
2 |
|
∫ exp |
|
dt |
|
|
|
|||||||||||||||||
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
−∞ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
так |
|
что |
|
параметр |
σ 2 |
нормального |
распределения |
является |
дисперсией |
|||||||||||||||||||||||||
D(ξ)=σ 2 .
Центральный момент четвертого порядка вычислим по методу дифференцирования интеграла по параметру. Для этого в качестве дифференцируемого интеграла используем интеграл Эйлера-Пуассона
|
|
|
|
|
|
∞ |
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
I0 |
(h)≡ ∫e−h2 x2 dx = |
π |
, h = |
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
2h |
|
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда центральный момент четвертого порядка |
|
|
|
|
|
|
||||||||||
μ4 |
= |
1 |
∞ |
|
(x − a)2 |
1 |
|
∂ |
1 ∂ |
I0 |
|
= |
3 π |
= 3σ 4 |
||
σ 2π |
∫ |
(x − a)4 exp − |
|
2 |
dx = − |
σh |
2π |
− |
2h ∂h |
(h) |
5 |
|||||
|
|
−∞ |
|
2σ |
|
∂h |
|
|
4h |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
σ 2π |
|
|||
и, следовательно, коэффициент эксцесса нормального распределения
Ek = σμ44 −3 = 0 .
