Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

g3

.pdf

Скачиваний:

Добавлен:

25.03.2016

Размер:

388.89 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Пример. Бомбардировщик, пролетевший вдоль моста через реку Томь, длина которого 30 м и ширина 8 м, сбросил бомбы. Случайные величины ξ и η независимы и распределены нормально со среднеквадратичными отклонениями, соответственно равными 6 и 4 м, математическими ожиданиями, равными 0. Здесь ξ – случайная величина расстояния от вертикальной оси симметрии моста до места падения бомбы; η – случайная величина расстояния от горизонтальной оси симметрии моста до места падения бомбы. Найти: 1) вероятность попадания в мост одной бомбы; 2) вероятность разрушения моста, если сброшены 2 бомбы, причем известно, что для разрушения моста достаточно одного попадания.

Решение. Вероятность попадания одной бомбы равна

P[(ξ,η) D]= ∫∫ f (x, y)dxdy .		(1)
	D
Так как ξ и η независимы, то f (x, y)= fξ (x)fη(y). По условию задачи область
интегрирования ограничена следующими линиями:
x =15,	y = 4	(2)
D :	y = −4
x = −15,

Тогда из (1) с учетом (2) получим

P[(ξ,η) D]= 15∫ fξ (x)dx 4∫ fη(y)dy = 21π σ∫ξ −15 −4 −15

σξ

= [Φ1(2.5)− Φ1(− 2.5)][Φ1(1)− Φ1(−1)]= 0.6741

exp−

t2 2

			4

		σ		η
				η
dt			∫
	−			4
	−		ση
			ση


	t2
	t2		=
exp−	2	dt	=
	2

Для получения ответа на вторую часть вопроса задачи введем обозначения: A1– событие, состоящее в попадании в цель первой бомбы; A2 – событие, состоящее в попадании в цель второй бомбы. Тогда вероятность попадания в мост хотя бы одной бомбы по теореме сложения вероятностей совместных событий и теореме умножения вероятностей независимых событий равна

P(A1 + A2 )= P(A1)+ P(A2 )− P(A1)P(A2 )= 2 0.6741 − (0.6741)2 = 0.8938 .

§6. Распределения Вейбулла, Рэлея, показательное

Определение. Распределение непрерывной (СВ) ξ называют показательным, если соответствующая ей плотность распределения выражается формулой

		fξ (x, λ)=	0, x < 0
		fξ (x, λ)=			−λx			,
					−λx		, x ≥ 0
			λe				, x ≥ 0
где λ	–	параметр распределения,			который одновременно определяет моду
этого распределения Mo = λ . Функция показательного распределения равна
		F (x, λ)=	x	f		(x, λ)dx =		0, x	< 0
		F (x, λ)=	∫	f	ξ	(x, λ)dx =
		ξ			ξ				−λx
									−λx	, x ≥ 0
			−∞					1 − e		, x ≥ 0
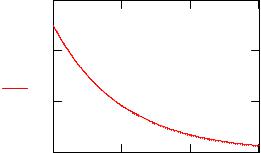
График плотности показательного распределения представлен на Рис. 4.
		0.6
		0.4
		f(x,λ)
		0.2
		00	2				4	6
						x			f (x, 0.5).
		Рис. 4. Показательное распределение							f (x, 0.5).
Числовые характеристики показательного распределения:

∞

M (ξ)= λ ∫xe−λxdx =

∫te

−tdt =

∞

−1 ∞

D(ξ)=

λ ∫

e−λxdx

∫t2e−tdt

−

, σ =

−1

∞

−λx

−1

∞

−t

μ3

∫

= λ

−

dx =

t e

= 2

−1

∞

−λx

−1

∞

−t

μ4

∫

= λ

−

dx =

dt =

−3

= 6 .

−1

Из определяющего медиану условия

Me	∞	1
P(ξ < Me)= λ ∫e−λxdx =1	− e−λMe = P(ξ > Me)= λ ∫e−λxdx = e−λMe =	1	,
0	Me	2
0	Me

следует, что медиана показательного распределения равна

Me = lnλ(2).

Показательный закон используется в теории надежности, в которой надежность устройства характеризуется функцией надежности. Функцией надежности R(t) называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t :

R(t)= P(T > t)=1− F(t).

Для показательного закона R(t)= P(T > t)=1− F(t)= e−λt . Показательный закон удобен тем, что он обладает следующим свойством: вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t .

Для доказательства этого свойства введем обозначения событий:

А – безотказная работа элемента на интервале (0,t0 ) длительностью t0 ; В – безотказная работа элемента на интервале (0,t0 +t) длительностью t . Тогда АВ – безотказная работа элемента на интервале (t0,t0 +t) длительностью t0 +t

. Вероятности этих событий определяются функцией надежности и равны

P(A)= e−λt0 , P(B)= e−λt , P(AB)= e−λ(t0 +t),

откуда найдем условную вероятность того, что элемент будет работать безотказно на интервале (t0,t0 +t) при условии, что он уже проработал

безотказно на предшествующем интервале (0,t0 ),

P(B / A)= PP((ABA))= e−λt .

Полученная формула не содержит t0 , так что время работы на

предшествующем интервале не сказывается на величине вероятности безотказной работы на последующем интервале, что и требовалось показать. Можно показать, что таким свойством обладает только показательное распределение. Это означает, что если на практике изучаемая величина этим свойством обладает, то она распределена по показательному закону.

Определение. Распределение непрерывной (СВ) ξ называют распределением Рэлея, если соответствующая ей плотность распределения выражается формулой

0, x < 0
fξ (x, λ)=	3	x2e−λx	,
	λ	x2e−λx	, x ≥ 0
2

где λ – параметр распределения. Функция распределения Рэлея равна

x	0,		x < 0
x
Fξ (x, λ)= ∫ fξ (x, λ)dx =				1 + (1 +	λx)2		−λx
−∞		−				e	−λx	, x ≥ 0
−∞	1	−	2			e		, x ≥ 0
			2

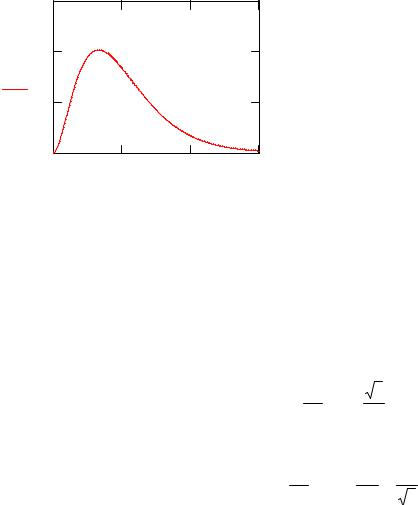
График плотности распределения Рэлея представлен на Рис. 5.

0.6
0.4
f(x,λ)
0.2
0	0	2	4	6
			x
Рис. 5. Распределение Рэлея				f (x,1.5).

Числовые характеристики распределения Рэлея:

∞

M (ξ)

= λ

∫x3e

−λxdx

∫t3e

−tdt =

2λ

∞

−λx

−t

D(ξ)=

∫

−

dx =

∫t

(t −3)

dt =

2λ2

λ2

3 ∞

3 3

−λx

∞

−t

μ3

∫

x −

∫t

−

2λ3

λ3

, σ = λ3 ,

As = σμ33 = 23 ,

∞

−λx

∞

−t

μ4

∫

x −

dx =

∫t

(t −3) e

dt =

, Ek

−3

= 2 .

2λ4

λ4

σ 4

Из определяющего моду необходимого условия экстремума f ′(x)= 0 нетрудно найти моду Mo = λ2 . Из определяющего медиану условия

P(ξ < Me)= F (Me)= P(ξ > Me)=1 − F(Me)= 12 ,

следует уравнение, неявно задающее медиану

	1	+ (1	+ λMe)2		1
					1
F(Me)=1 −				e−λMe =		.
F(Me)=1 −			2	e−λMe =	2	.
			2		2

Распределение Рэлея находит широкое применение в теории стрельбы и статистической теории связи.

Определение. Непрерывная (СВ) ξ имеет распределение Вейбулла, если соответствующая ей плотность распределения выражается формулой

0, x ≤ x0

(x,α,σ

α−1

, x

)= α

x − x

x > 0

exp

−

σ0

где α,σ0, x0 – параметры распределения.

Распределение Вейбулла находит

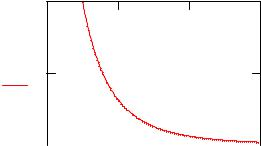
применение в задачах долговечности и надежности. График плотности распределения Вейбулла представлен на Рис. 6.

	1
f(x,1	,1)
f(x,2	,1)0.5
	0	0	1	2	3	4
				x

Рис. 6. Плотность распределения Вейбулла при σ =1, x0 = 0 для значений α =1 – сплошная линия, и α = 2 – пунктирная кривая.

Распределение Вейбулла имеет следующие числовые характеристики:

					1		2				2		2				1					1/ α
M (ξ)= x +σ	0	Γ 1	+			, D(ξ)=σ		Γ 1	+			−Γ		1	+			, Me = x	0	+σ	0	(ln(2))

0				α			0			α						α

1 1/ α

Γ 1

−3Γ 1

Γ 1

+ 2Γ

Mo = x0

+σ0

−

, α ≥1, As =

3 / 2

Γ 1

− Γ

§7. Распределение Парето

Определение. Непрерывная (СВ) ξ		имеет	распределение Парето с
параметрами a,b > 0 , если соответствующая ей			плотность распределения
выражается формулой
0, x < a
fξ (x)=	b	.
b a	,	x ≥ a
	,	x ≥ a
x x

График плотности распределения Парето представлен на Рис. 7.

f(x) 0.5

0
0	2	4	6	8
			x

Рис. 7. Плотность распределения Парето при a = 3,b = 3 .

Распределение Парето используется в экономике для описания величины дохода, причем параметр a – минимально возможный доход.

§8. Логистическое распределение

Определение. Непрерывная (СВ) ξ имеет логистическое распределение, если соответствующая ей плотность распределения выражается формулой

			(x −a)
		exp −
		exp −		b
fξ (x)=				b	, b > 0, a R..
fξ (x)=				(x −a) 2	, b > 0, a R..
	b 1	+exp −
	b 1	+exp −		b
				b

График плотности логистического распределения представлен на Рис. 8.

	0.1
f(x)	0.05
	0	0	2	4	6	8
				x

Рис. 8. Плотность логистического распределения при a = 0,b =1.

Логистическое распределение часто используется вместо нормального распределения при исследовании медико-биологических объектов.

§9. Характеристические функции

Простое решение многих задач теории вероятностей удается получить с помощью характеристических функций. Теория характеристических функций развита в курсе математического анализа в разделе «Ряды и

интегралы Фурье».		gξ (t) (СВ) ξ называют
Определение. Характеристической функцией		gξ (t) (СВ) ξ называют
функцию вида
	itξ
gξ (t)= M e		,

где i – мнимая единица;

t –

параметр,

являющийся

аргументом

характеристической функции,

itξ

математическое ожидание (СВ) e

itξ

M e

–

Если ξ – непрерывная (СВ), то

g (t)=

itξ

∞

itx

(x)dx ,

(1)

M e

∫

а если ξ – дискретная (СВ), то

−∞

gξ (t)=

itξ

∞

itx j

Pj .

(2)

M e

∑e

j=1

Преобразование (1), которому нужно подвергнуть плотность распределения fξ (x), чтобы получить gξ (t) называется преобразованием Фурье. В разделе

«Ряды и интегралы Фурье» курса математического анализа доказывается, что если gξ (t) выражается через fξ (x) с помощью преобразования Фурье, то, в

свою очередь, fξ (x) выражается	через gξ (t) с помощью обратного
преобразования Фурье
f (x)=	1	∞e−itxg (t)dt .
f (x)=	2π	∞e−itxg (t)dt .
ξ	2π	∫	ξ
ξ			ξ

−∞

Непосредственно из определения характеристической функции, свойств математического ожидания и условия нормировки следует, что характеристические функции обладают следующими свойствами:

Свойство 1. Если (СВ) ξ и η связаны линейно η = aξ + b ,

gη (t)= gξ (at)eibt

Свойство 2. Если (СВ) ξ и η – независимы, то для (СВ) χ = ξ +η ,

gχ (t)= gξ (t)gη(t).

Свойство 3.

(0)=1,

(t)

≤1,

d k gξ (0)

= ikν

dxk

Пример. Найти характеристическую функцию для случайной величины, распределенной по биномиальному закону.

Решение. По формуле Бернулли

P(ξ = k)= Ckn pkqn−k .

Тогда по определению характеристической функции и с учетом формулы бинома Ньютона

itk

n−k

gξ (t)= ∑e

P(ξ = k)= ∑e

Ck p

= ∑

e p

Ck q

+q .

k=0

Пример. Найти характеристическую функцию для случайной величины, распределенной по закону Пуассона.

Решение. По формуле Пуассона

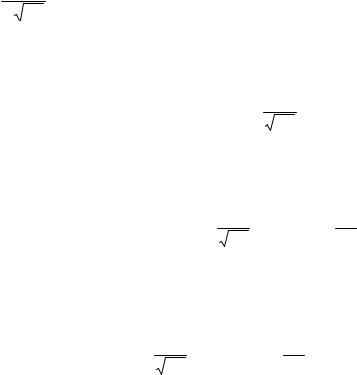
P(ξ = k)= λkk! e−λ .

Тогда по определению характеристической функции

∞

itk λk

−λ

gξ (t)= ∑ e

∑

= e

= exp λ e

−1 .

k=0

Пример. Найти характеристическую функцию равномерной на отрезке [a,b] случайной величины.

Решение. По определению характеристической функции для непрерывной

случайной величины с плотностью распределения f (x)=									1		, x [a,b]
случайной величины с плотностью распределения f (x)=											, x [a,b]
								ξ	b −a
									b −a
	∞				1	b		eitb −eita
g (t)=		eitx f		(x)dx =	1		eitxdx =	eitb −eita		.
g (t)=	∫	eitx f		(x)dx =	b −a ∫		eitxdx =			.
ξ	∫		ξ		b −a ∫			it(b −a)
	−∞					a

Пример. Найти характеристическую функцию случайной величины, распределенной по нормальному закону.

Решение. По условию задачи плотность распределения имеет нормальный

вид f (x)=

exp −

−a)2

. По теореме о функции (СВ) для (СВ) η = ξ −a

2π

2σ

плотность распределения равна

(y)= x′

(yσ +a)= 1 e−

2π

Тогда по определению характеристической функции

gη(t)=

∞

ity

(y)dy =

∞

∫

∫e

fη

2π

exp ity −

dy .

−∞

Продифференцируем обе части последнего равенства по t

′

∞

∫

gη(t)

2π

y exp ity − 2

dy .

−∞

Откуда, интегрируя по частям, получим

∞

(t)=

−i

∞

−

−i

ity−

∞

g′

−it

∫

exp[ity]d e

∫

2π

−∞

Решение полученного уравнения gη′ (t)= −tgη(t) gη(0)=1 имеет вид

	−	t2
g	−	2 .
g	(t)= e	2 .
η


		y	2
exp		y		dy	= −tgη(t).

	ity −	2
		2

с начальным условием

Так как ξ = ση + a , то по свойству характеристических функций

	ita		σ	2 2
gξ (t)= e	ita		σ	t	,
gξ (t)= e		gη(σt)= exp ita −		2	,
				2

что и требовалось получить.

§10. χ2 -распределение

Определение. Непрерывная случайная величина ξ имеет χ2 - распределение с m степенями свободы, если плотность ее распределения выражается формулой

0, x ≤ 0

−1

fξ (x, m)=

x 2

exp

−

, x > 0 .

График плотности χ2 - распределения представлен на Рис. 9.
	2
	1.5
f(x,3)
f(x,1)	1
	0.5
	0	0	5	10	15
				x

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.08.20194.27 Mб39Freon_Thermodinamic_diagrams_i_lgP.doc
#
29.05.20151.25 Mб29FTI_Lekcii_po_osnovam_fiziki_plazmy.pdf
#
16.09.20197.33 Mб350Full.doc
#
15.11.20194.13 Mб10Full.docx
#
25.03.2016519.27 Кб10g2.pdf
#
25.03.2016388.89 Кб7g3.pdf
#
25.03.2016254.16 Кб6g4.pdf
#
25.03.2016387.94 Кб5g5.pdf
#
25.03.2016385.49 Кб6g6.pdf
#
29.05.20151.09 Mб84geokniga-трещиноватость-горных-пород.pdf
#
02.12.20181.74 Mб10Geology.doc