
g3
.pdf
Рис. 9. Плотность χ2 - распределения для различных степеней свободы m : при m =1– пунктирная линия; при m = 3 – сплошная линия.
Применение χ2 - распределения основано на его интерпретации как распределения суммы квадратов m независимых (СВ), распределенных по закону N(0,1). Докажем это утверждение.
Теорема. Если m независимых (СВ) ξ j, j =1,2,...m одинаково распределены по
закону N(0,1), |
то (СВ) χ2 |
|
m |
2j |
имеет χ2 - распределение. |
|
|||||||
= ∑ξ |
|
||||||||||||
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
Доказательство. По условию теоремы |
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
x |
2 |
|
|
|
|
f |
|
(x)= |
|
|
|
− |
|
|
. |
(1) |
||
|
|
|
2π |
exp |
2 |
|
|||||||
|
ξj |
|
|
|
|
|
|
|
|||||
|
обозначения: η = ξ2 , |
|
|
|
|
|
|
|
|||||
Введем |
x – |
|
возможные значения |
(СВ) ξ ; y – |
|||||||||
возможные значения (СВ) η . Найдем плотность |
fη(y). |
Для этого найдем |
|||||||||||||||||||||||||||
соответствующую ей функцию распределения |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Fη(y)= P(η |
< y)= |
|
2 |
|
|
= P(− |
y < ξ |
< |
y )= Fξ |
( |
y )− Fξ (− |
|
y ).(2) |
||||||||||||||
|
|
P ξ |
|
< y |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда с учетом (1) плотность распределения (СВ) η принимает вид |
|
|
|||||||||||||||||||||||||||
f |
(y)= |
dFη(y) |
= |
1 |
f |
|
( y )+ |
|
1 |
|
f |
|
(− |
y )= |
1 |
|
|
|
y |
|
(3) |
||||||||
|
|
dy |
|
|
ξ |
2 |
|
|
ξ |
|
exp − |
2 |
, y > 0 . |
|
|||||||||||||||
η |
|
|
|
|
|
2 |
|
y |
|
|
y |
|
|
|
|
2πy |
|
|
|
|
|
||||||||
Учитывая (3), для плотности fη(y) найдем характеристическую функцию |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Γ |
1 |
|
|
|
|
|
|
|
∞ |
|
ity |
|
|
|
|
|
1 |
|
|
∞ |
|
1/ 2−1 |
−t |
|
|
|
|
|
|
1 |
|
|
||||
f |
(t)= |
|
∫ |
e |
f |
(y)dy = |
|
|
|
∫ |
t |
dt = |
|
|
2 |
= |
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
||||||||||||||
η |
|
|
|
|
η |
|
|
|
π(1 − 2it) |
|
|
|
|
|
|
|
π(1 − 2it) |
|
(1 − 2it) |
|
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
откуда по свойству характеристических функций для (СВ) χ2 = ∑η j |
имеем |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fχ2 (t)= ∏ fηj (t)= |
|
|
|
. |
|
|
|
|
|
(4) |
||||||||||
|
|
|
|
|
|
|
|
|
(1−2it)m / 2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (4) с помощью обратного преобразования Фурье получим
|
|
∞ |
|
|
|
∞ |
|
−itz |
m |
−1 − |
z |
|
− |
n |
|
|
|
m |
−1 − |
z |
|
|
|
||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
|
2 |
|
|
||||||||||||||
|
1 |
|
|
1 |
e |
e |
i |
|
e |
|
|
|
|||||||||||||||||
fχ2 (z)= |
∫e |
−itz fχ2 |
(t)dt = |
∫ |
|
dt = |
z |
|
|
∫t |
2 etdt = |
z |
|
|
|
|
, |
||||||||||||
π |
π |
|
m / 2 |
|
|
m |
|
|
m |
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
0 |
(1 − 2it) |
|
|
|
|
|
C |
|
|
|
|
|
|
m |
|
||||||||
|
|
|
|
|
π 2 2 |
|
|
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Γ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
что и требовалось доказать.
χ2 - распределение имеет следующие числовые характеристики:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ m −x |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
||||||||||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
∞ |
|
|
|
|
|
2Γ |
|
|
|
|
+ |
1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−t |
|
|
2 |
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
|
|
(x)dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
x 2 e 2 dx = |
|
|
∫ |
t 2 e |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
M χ |
= |
xf |
χ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt = |
|
|
|
|
|
|
|
|
= m, |
|
|||||||||||||||||||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
m |
|
|
|
m |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
m 0 |
|
|
|
|
|
|
|
|
|
|
|
Γ |
|
|
0 |
|
|
|
|
|
|
|
|
Γ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
∞ |
|
|
|
|
2 |
|
|
m |
−1 |
− |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
D |
χ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
(x − m) |
|
x |
2 |
|
e |
|
|
2 dx = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m2 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
Γ |
|
+ 2 |
− mΓ |
+1 |
+ |
|
|
Γ |
|
|
= 2m |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
m |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из условия экстремума |
|
|
|
|
|
|
|
|
|
|
2 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
f |
′ |
|
|
|
|
= |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
следует, |
что мода для χ - |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
(x) |
|
|
|
|
|
|
|
|
− 2 f (x)= 0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распределения равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mo = m −2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§11. Распределение Фишера |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Определение. |
Непрерывная |
|
случайная |
величина ξ |
|
|
имеет |
|
|
распределение |
|||||||||||||||||||||||||||||||||||||||||||||||||
Фишера с m1 и m2 степенями свободы, если плотность ее распределения выражается формулой
|
|
|
|
0, x ≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
m1 |
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
m1 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
m1 |
+m2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f |
ξ |
(x, m , m |
2 |
)= |
|
|
|
|
x |
|
|
|
|
|
|
|
m1 |
|
− |
|
2 |
. |
||||
|
1 |
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
|
x |
|
|
|
, x > 0 |
|||||||
|
|
|
|
|
|
m |
m |
2 |
|
|
m |
|
|
|
|
|||||||||||
|
|
|
|
|
|
B |
|
1 |
, |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
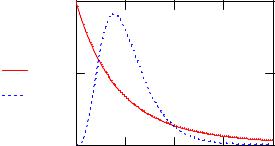
График плотности распределения Фишера представлен на Рис. 10.
1 |
|
|
|
|
|
f(x,2,10) |
|
|
|
|
|
f(x,10,50)0.5 |
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
4 |
|
|
|
x |
|
|
Рис. 10. Плотность распределения Фишера для различных степеней свободы m1, m2 : при m1 =10, m2 = 50 – пунктирная линия; приm1 = 2, m2 =10 – сплошная линия.
Применение распределения Фишера основано на следующей теореме.
Теорема. Если ξ и η – независимые (СВ), |
имеющие χ2 - распределение |
||||||||||||||||||||||||||||||||||
соответственно с m |
и m |
степенями свободы, то (СВ) F = ξ m2 |
подчиняется |
||||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η m1 |
|
распределению Фишера с (m1, m2 ) степенями свободы. |
|
||||||||||||||||||||||||||||||||||
Доказательство. По условию теоремы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0, x ≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
fξ |
(x, m1)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
exp − |
|
|
, |
x > 0 , |
(1) |
|||||||||
|
|
m |
|
|
|
m |
|
|
|
|
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
Γ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0, x ≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|||||||
fη |
(y, m2 ) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
y |
|
(2) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
exp |
− |
|
|
, y > 0 . |
||||||||||
|
|
m |
|
|
|
m |
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть x – возможные значения (СВ) |
ξ ; y – возможные значения (СВ) η ; z – |
||||||||||||||||||||||||||||||||||
возможные значения (СВ) |
F . Тогда z = |
m2 |
|
x |
|
и, следовательно, |
|
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
y |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
1 |
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
x = |
|
zy, x′z = |
|
|
y . |
|
|
|
|
|
(3) |
||||||||||||||||||||
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из условия нормировки
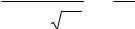
∞ |
∞∞ |
∫ fF (z)dz = ∫ ∫ fξ (x)fη(y)dxdy =1 |
|
0 |
0 0 |
с учетом равенств (1-3) следует, что
|
|
|
|
|
|
|
∞ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
∞ |
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
(x)fη(y)dy = m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
fF (z)= ∫xz fξ |
|
∫yfξ m |
|
zy fη(y)dy = |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
m1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
m1 |
|
2 |
z |
|
|
|
|
|
|
|
|
|
∞ |
|
m |
+m |
−1 |
|
|
|
|
y |
|
|
|
|
m |
|
||||||||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
∫y |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||
= |
|
|
m1 +m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp − 2 |
|
+ m |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
z dy = |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
Γ |
1 |
|
Γ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
m1 |
|
|
m1 |
|
|
m1 |
−1 |
|
|
|
|
m1 |
|
|
− m1 +m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
m1 |
+m2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1+ m |
|
|
|
|
|
|
∞ |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
−1 |
|
−t |
|
||||||||||||||||||
= |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
∫t |
|
|
|
|
|
|
|
e |
dt = |
||||||||
|
|
|
|
|
|
|
|
|
m |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Γ |
|
1 |
Γ |
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
m1 |
|
|
2 |
|
Γ m1 +m2 |
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
m1 +m2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
−1 |
|
|
|
m1 |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
m2 |
|
|
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
1 |
+ |
z |
|
|
|
2 |
|
|
, |
|
|
|
|
|
|||||||||||||||
|
|
m |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Γ |
1 |
Γ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
что и требовалось доказать.
Математическое ожидание и дисперсия распределения Фишера определяются по формулам
|
m2 |
|
2m2 |
(m + m − 2) |
|
|
||||
M (F )= |
> 2 , D(F )= |
|
2 |
1 |
2 |
|
, m2 |
> 4 . |
||
|
, m2 |
|
|
|
||||||
m2 − 2 |
m |
(m − 2)2 (m − 4) |
||||||||
|
|
|
1 |
2 |
2 |
|
|
|
||
|
§12. Распределение Стьюдента |
|
|
|||||||
Определение. Непрерывная |
случайная величина |
ξ имеет |
распределение |
|||||||
Стьюдента с m степенями свободы, если плотность ее распределения выражается формулой
|
|
m +1 |
|
|
|
|
|
− |
m+1 |
|
||||||
|
Γ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
x |
2 |
|
|
|||||||
|
|
|
2 |
|
|
|
|
|||||||||
fξ (x, m)= |
|
|
|
|
|
|
+ |
|
|
|
|
, − ∞ < x < ∞. . |
||||
m |
|
|
|
1 |
m |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Γ |
|
|
|
|
πm |
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
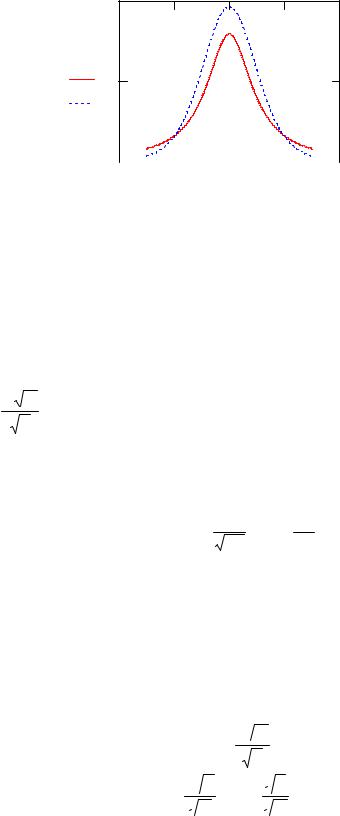
График плотности распределения Стьюдента представлен на Рис. 11.
0.4
f(x,1)
f(x,8)0.2
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
0 |
2 |
4 |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
Рис. 11. Плотность распределения Стьюдента для различных степеней свободы m : при m = 8 – пунктирная линия; при m =1– сплошная линия.
|
Применение распределения Стьюдента основано на следующей |
|||||||||||||||||||
теореме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. Если ξ и η – независимые (СВ), причем ξ |
имеет распределение |
|||||||||||||||||||
N(0,1), а η – |
χ2 - распределение соответственно с m степенями свободы, то |
|||||||||||||||||||
(СВ) |
T = ξ |
m |
подчиняется |
|
распределению |
|
|
|
Стьюдента с |
m степенями |
||||||||||
|
η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
свободы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. По условию теоремы |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
fξ (x)= |
1 |
|
|
|
x |
2 |
|
|
(1) |
||||||
|
|
|
|
|
|
exp− |
|
|
, |
|
||||||||||
|
|
|
|
|
|
|
|
|
2π |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, y ≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
−1 |
|
|
|
|
y |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
fη(y, m)= |
|
|
|
|
|
y 2 |
exp − |
|
|
|
, y > |
0 . |
(2) |
||||
|
|
|
|
m |
m |
|
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть x – возможные значения (СВ) ξ ; y –
возможные значения (СВ) T . Тогда z = x ym x = z
ym x = z
 my , x′z =
my , x′z = 
Из условия нормировки
возможные значения (СВ) η ; z –
и, следовательно,
my . (3)
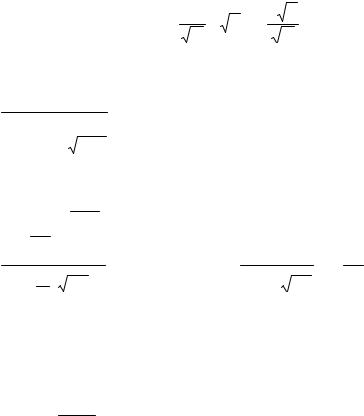
∞ |
∞∞ |
|
|
|
|
∫ fT (z)dz = ∫ ∫ fξ (x)fη(y)dxdy =1 |
|||||
0 |
0 0 |
|
|
|
|
с учетом равенств (1-3) следует, что |
|
|
|
|
|
∞ |
|
1 |
∞ |
z |
y |
fT (z)= ∫x′z fξ (x)fη(y)dy = |
|
∫ |
|
|
|
m |
y fξ |
fη(y)dy = |
|||
0 |
|
0 |
|
m |
|
|
|
|
|
||
= |
m |
|
1 |
|
|
m |
|
||||
|
2 |
||||
2 |
Γ |
|
2πm |
||
2 |
|||||
|
|
|
|
||
1 + z2 − m2+1 = m
Γ m πm2
∞ |
m−1 |
|
y |
|
|
z |
2 |
|
|
|
|
|
|||||||
∫y |
2 |
|
exp − |
1 |
+ |
|
dy = |
||
|
2 |
m |
|||||||
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
m+1 |
|
|
|
m +1 |
|
|
|
|
− |
m+1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
∞ |
|
|
|
−1 |
|
−t |
Γ |
|
2 |
|
|
|
|
z |
2 |
2 |
|
|
||
2 |
|
|
|
|
|
|||||||||||||||
∫t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
e |
dt = |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
, |
|
|
|
|
|
m |
|
|
1 |
m |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
Γ |
|
|
πm |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
что и требовалось доказать. Распределение Стьюдента обладает следующими числовыми характеристиками:
M (ξ)= 0, D(ξ)= mm− 2 (m > 2), As = 0 (m > 3), Mo = Me = 0.
