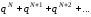- •Глава Числовые ряды
- •§ 1. Определение числового ряда и основные теоремы
- •§2. Достаточные признаки сходимости знакопостоянных рядов
- •§3.Знакочередующиеся и знакопеременные ряды
- •§4. Некоторые применения теория числовых рядов
- •Степенные ряды.
- •§ 1 Основные определения
- •§ 2. Степенные ряды
- •§ 3 Разложение функций в ряды
- •§ 4. Приложение степенных рядов
- •§ 5. Тригонометрические ряды Фурье
§2. Достаточные признаки сходимости знакопостоянных рядов
Ограничимся
рассмотрением лишь знакоположительных
рядов, т.е. всякий знакоотрицательный
ряд можно преобразовать в знакоположительный
простым умножением на
 .
.
Теорема 2.1.
Пусть дан знакоположительный ряд
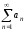 .
Если последовательность его частных
сумм ограничена сверху, то ряд сходится.
.
Если последовательность его частных
сумм ограничена сверху, то ряд сходится.
Доказательство.
Составим частичные суммы
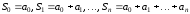 .
.
Последовательность
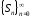 монотонна:
монотонна: .
По условию
.
По условию ограничена сверху, например числом А.
Тогда последовательность
ограничена сверху, например числом А.
Тогда последовательность (по теореме о пределе монотонной
последовательности) имеет предел. По
определению 1.3. это означает, что ряд
сходится. Теорема доказана.
(по теореме о пределе монотонной
последовательности) имеет предел. По
определению 1.3. это означает, что ряд
сходится. Теорема доказана.
Все признаки сходимости положительных рядов, в конечном счете, основаны на этой теореме.
Теорема 2.2.
(Критерий Коши)
Для того, чтобы ряд
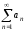 сходился, необходимо и достаточно, чтобы
сходился, необходимо и достаточно, чтобы и
и натурального
натурального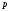 выполнялось неравенство
выполнялось неравенство .
.
Практическое
применение критерия Коши бывает связано
с большими трудностями, но его иногда
полезно использовать для доказательства
расходимости ряда: если найдутся хотя
бы одно значение
 и одно натуральное
и одно натуральное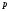 такие, что
такие, что
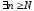 ,
но
,
но
 для
для ,
то ряд
,
то ряд расходится. Покажем это на примере.
расходится. Покажем это на примере.
Пример 1. Покажем
расходимость ряда
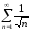 ,
хотя этот ряд удовлетворяет необходимому
признаку сходимости. Для доказательства
расходимости ряда
,
хотя этот ряд удовлетворяет необходимому
признаку сходимости. Для доказательства
расходимости ряда
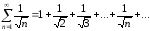 .
.
Оценим его
 –ю
частичную сумму:
–ю
частичную сумму:
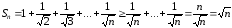 ;
; .
.
При
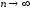 ,
, .
Ряд расходится.
.
Ряд расходится.
Рассмотренный ряд
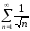 является частным случаем обобщенного
гармонического ряда
является частным случаем обобщенного
гармонического ряда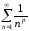 .
Далее будет показано, что обобщенный
гармонический ряд сходится при
.
Далее будет показано, что обобщенный
гармонический ряд сходится при и расходится при
и расходится при
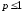 .
.
Пример 2. С помощью
критерия Коши покажем расходимость
ряда
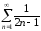 .
.
Для этого рассмотрим
 .
.
Существует ли
 и натуральное
и натуральное такие, что данная сумма была не меньше
такие, что данная сумма была не меньше ?
Положим
?
Положим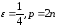 .
Тогда
.
Тогда
![]() ;
по критерию Коши ряд расходится.
;
по критерию Коши ряд расходится.
Теорема 2.3 (первый признак сравнения). Даны ряды
|
|
(1) |
|
|
(2) |
с
положительными членами, причем начиная
с некоторого номера
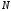 для всех членов этих рядов выполняется
неравенство
для всех членов этих рядов выполняется
неравенство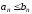 .
Тогда
.
Тогда
из сходимости ряда (2) следует сходимость ряда (1);
из расходимости ряда (1) следует расходимость ряда (2).
Доказательство.
Обозначим через
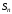 частичную сумму ряда
частичную сумму ряда (1), а через
(1), а через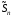 –
частичную сумму ряда
–
частичную сумму ряда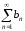 (2). Ряд (2) сходится, поэтому
(2). Ряд (2) сходится, поэтому ограничена. Так как по условию теоремы
ограничена. Так как по условию теоремы ,
то
,
то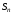 также ограничена, а следовательно и
ряд (1) сходится по теореме 2.1.
также ограничена, а следовательно и
ряд (1) сходится по теореме 2.1.Так как ряд (1) расходится, а по условию каждый член ряда (2) больше или равен соответствующему члену ряда (1), начиная с некоторого номера
 ,
то частичные суммы ряда (2) не ограничены,
следовательно, ряд (2) расходится.
,
то частичные суммы ряда (2) не ограничены,
следовательно, ряд (2) расходится.
Теорема доказана.
Пример 3. Исследовать
на сходимость ряд
 .
.
Сравним данный
ряд с гармоническим рядом
 .
Так как для любого
.
Так как для любого верно неравенство
верно неравенство и гармонический ряд расходится, то по
первому признаку сравнения исходный
ряд тоже расходится.
и гармонический ряд расходится, то по
первому признаку сравнения исходный
ряд тоже расходится.
Теорема 2.4. (второй
признак сравнения).
Пусть даны знакоположительные ряды
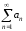 (1)
и
(1)
и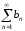 (2).
(2).
Если существует конечный и отличный от нуля
 ,то
оба ряда сходятся или расходятся
одновременно.
,то
оба ряда сходятся или расходятся
одновременно.
Если
 ,то
из сходимости ряда (2) следует сходимость
ряда (1).
,то
из сходимости ряда (2) следует сходимость
ряда (1).
Доказательство.
По условию теоремы
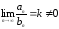 .
По определению предела это означает,
что
.
По определению предела это означает,
что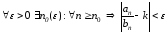 ,
то есть
,
то есть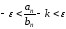 ,
или
,
или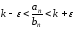 ,
, .
Отсюда, используя свойство об умножении
членов ряда на постоянную и 1 признак
сравнения, получаем утверждение теоремы.
.
Отсюда, используя свойство об умножении
членов ряда на постоянную и 1 признак
сравнения, получаем утверждение теоремы.
Чтобы применять признаки сравнения, необходимо иметь некоторый набор рядов, сходимость которых изучена, и с которыми можно сравнивать исследуемый ряд. В роли таких «эталонных» рядов используют:
Гармонический ряд
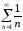 .
Этот ряд расходится.
.
Этот ряд расходится.Ряд
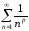 .
Этот ряд называютобобщенным
гармоническим рядом
(или рядом
Дирихле).
Он расходится при
.
Этот ряд называютобобщенным
гармоническим рядом
(или рядом
Дирихле).
Он расходится при
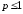 и сходится при
и сходится при .
.Ряд геометрической прогрессии
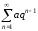 .
Этот ряд сходится при
.
Этот ряд сходится при и расходится при
и расходится при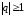 .
.
Пример 4. Исследовать
на сходимость ряд
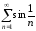 .
.
Сравним данный
ряд с рядом
 .
Воспользоваться первым признаком
сравнения мы не сможем. Рассмотрим
.
Воспользоваться первым признаком
сравнения мы не сможем. Рассмотрим =1.
=1.
Так как
 ,
то по второму признаку сравнения ряды
,
то по второму признаку сравнения ряды и
и ведут себя по отношению к сходимости
одинаково. Следовательно, ряд
ведут себя по отношению к сходимости
одинаково. Следовательно, ряд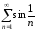 расходится.
расходится.
Сравним поведение
двух рядов, являющихся частными случаями
обобщенного гармонического ряда (ряда
Дирихле) при
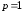 и
и![]() :
: ,
,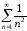 .
.
Представим себе,
что перед нами лежат две бесконечные
колоды карт. Берем карты из первой колоды
и выкладываем их так: первая карта вся,
рядом с ней половина второй карты, далее
третья часть третей карты и т.д.:
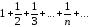 .
Так как ряд
.
Так как ряд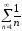 расходится, то в этом случае площадь
выложенных карт будет бесконечной. Если
же карты выкладывать чуть-чуть иначе:
первую – полностью, рядом с ней –
четверть второй карты, дальше
расходится, то в этом случае площадь
выложенных карт будет бесконечной. Если
же карты выкладывать чуть-чуть иначе:
первую – полностью, рядом с ней –
четверть второй карты, дальше третьей карты и так далее:
третьей карты и так далее: ,
то в этом случае площадь выложенных
карт будет конечной, так как ряд
,
то в этом случае площадь выложенных
карт будет конечной, так как ряд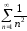 сходится, и его сумма равна
сходится, и его сумма равна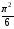 .
.
Пример 5. Исследовать
на сходимость ряд
 .
.
Т.к.
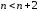 при
при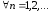 ,
то общий член данного ряда
,
то общий член данного ряда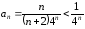 .
Ряд
.
Ряд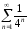 является сходящейся геометрической
прогрессией, где
является сходящейся геометрической
прогрессией, где .
Следовательно, наш ряд сходится по
теореме 2.3.
.
Следовательно, наш ряд сходится по
теореме 2.3.
Пример 6. Исследовать
на сходимость ряд
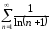 .
.
Т.к.
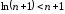 ,
, ,
то
,
то для
для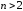 ;
;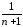 является общим членом расходящегося
гармонического ряда, так что поIпризнаку сравнения наш ряд расходится.
является общим членом расходящегося
гармонического ряда, так что поIпризнаку сравнения наш ряд расходится.
Пример 7. Исследовать
на сходимость ряд
 .
.
Сравним
 с общим членом гармонического ряда
с общим членом гармонического ряда ,
используя предельный признак сравнения:
,
используя предельный признак сравнения: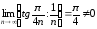 ,
по теореме 2.3. наш ряд расходится.
,
по теореме 2.3. наш ряд расходится.
Пример 8. Исследовать
на сходимость ряд
 .
.
Представим его
общий член в виде произведения общего
члена обобщенного гармонического ряда
и частного от деления
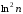 на некоторую положительную степень
на некоторую положительную степень ,
например, так:
,
например, так: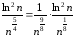 .
Найдем
.
Найдем

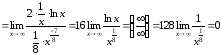 .
.
Поэтому,
начиная с некоторого номера,
 ,
следовательно, для достаточно больших
,
следовательно, для достаточно больших справедливо неравенство
справедливо неравенство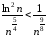 .
Ряд с общим членом
.
Ряд с общим членом сходится как обобщенный гармонический
ряд с показателем степени
сходится как обобщенный гармонический
ряд с показателем степени .
Следовательно, по теореме 2.3. наш ряд
сходится.
.
Следовательно, по теореме 2.3. наш ряд
сходится.
Недостаток обоих признаков сравнения в том, что их использование предполагает подбор второго ряда. Сделать это не всегда легко.
Существуют признаки сходимости, которые позволяют судить о сходимости ряда по его общему члену. К их числу относятся признаки Даламбера и Коши.
Теорема 2.5 (признак
Даламбера).
Пусть дан
 –знакоположительный ряд. Если существует
–знакоположительный ряд. Если существует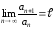 ,
то
,
то
при
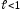 ряд сходится;
ряд сходится;при
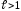 ряд расходится;
ряд расходится;при
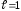 вопрос о сходимости ряда остается
открытым.
вопрос о сходимости ряда остается
открытым.
Доказательство.
Пусть
 .
По определению предела это означает,
что при достаточно большом
.
По определению предела это означает,
что при достаточно большом ,
, выполняется
неравенство
выполняется
неравенство
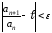 ,
где
,
где –
заранее заданное сколь угодно малое
положительное число. Отсюда
–
заранее заданное сколь угодно малое
положительное число. Отсюда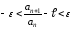 или
или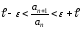 ,
,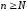 .
.
Пусть
 .
Возьмем
.
Возьмем столько малым, что
столько малым, что .
Обозначим
.
Обозначим ,
тогда
,
тогда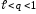 и
и
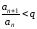 ,
откуда
,
откуда при
при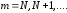 .
.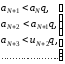 .
.
Итак члены ряда
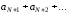 меньше
соответствующих членов геометрической
прогрессии, т.е.
меньше
соответствующих членов геометрической
прогрессии, т.е.
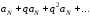 .
Так как
.
Так как ,
то последний ряд сходится, но тогда по
теореме 2.3. сходится и ряд
,
то последний ряд сходится, но тогда по
теореме 2.3. сходится и ряд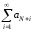 ,
и исходный ряд.
,
и исходный ряд.
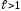 .
Тогда, из того что
.
Тогда, из того что
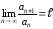 ,
следует, что (по определению пределов)
начиная с некоторого номера
,
следует, что (по определению пределов)
начиная с некоторого номера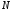 ,
для всех
,
для всех будет иметь место неравенство
будет иметь место неравенство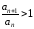 или
или
 .
Это означает, что члены ряда (1) возрастают,
начиная с номера
.
Это означает, что члены ряда (1) возрастают,
начиная с номера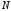 ,
то есть
,
то есть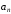 не стремится
к нулю, при
не стремится
к нулю, при
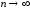 .
Следовательно ряд (1) расходится. Теорема
доказана.
.
Следовательно ряд (1) расходится. Теорема
доказана.
Пример 9. Исследовать
на сходимость ряд
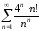 .
.
1) Воспользуемся признаком Даламбера. Имеем
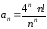 ,
,
,
,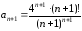

 .
.
Получившийся предел найдем с помощью второго замечательного предела. Для этого запишем его в виде
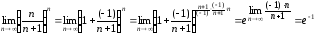 .
.
Таким образом, получили
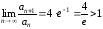 .
.
Следовательно, ряд расходится.
Пример 10. Исследовать
сходимость ряда
 .
.
Запишем
 и найдем
и найдем
 ,
то есть ряд расходится по признаку
Даламбера.
,
то есть ряд расходится по признаку
Даламбера.
Теорема 2.6.
(Радикальный признак Коши).
Пусть
 – знакоположительный ряд. Если существует
– знакоположительный ряд. Если существует ,
то
,
то
при
 ряд сходится;
ряд сходится;при
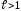 ряд расходится;
ряд расходится;при
 вопрос о сходимости ряда остается
открытым.
вопрос о сходимости ряда остается
открытым.
Доказательство.
Пусть
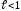 .
Рассмотрим число
.
Рассмотрим число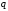 ,
удовлетворяющее соотношению
,
удовлетворяющее соотношению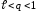 .
.
Из определения
предела и соотношения
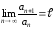 ,
следует, что существует такое число
,
следует, что существует такое число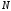 ,
такое что, для всех
,
такое что, для всех будет
иметь место неравенство:
будет
иметь место неравенство:
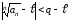

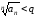
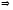
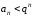 .
.
Рассмотрим теперь два ряда
|
|
(1) |
|
|
(3) |
Ряд (3) сходится, так как члены его образуют убывающую геометрическую прогрессию.
Члены ряда (1),
начиная с
 меньше членов
ряда (3) и следовательно, на основании
первого признака сравнения и свойства
(1) рядов, получаем что ряд (1) сходится.
меньше членов
ряда (3) и следовательно, на основании
первого признака сравнения и свойства
(1) рядов, получаем что ряд (1) сходится.
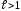 .
Тогда начиная с некоторого номера
.
Тогда начиная с некоторого номера
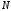 ,
для всех
,
для всех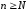 будет иметь место неравенство
будет иметь место неравенство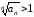 или
или
 .
Это означает, что члены ряда (1) возрастают,
начиная с номера
.
Это означает, что члены ряда (1) возрастают,
начиная с номера ,
то есть
,
то есть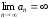 (
( не стремится
к нулю, при
не стремится
к нулю, при
 ).
Не выполнен необходимый признак
сходимости ряда. Поэтому ряд (1) расходится.
Теорема доказана.
).
Не выполнен необходимый признак
сходимости ряда. Поэтому ряд (1) расходится.
Теорема доказана.
Заметим, что признак
Коши сильнее признака Даламбера, так
как предел
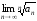 может существовать, а предел
может существовать, а предел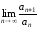 –
нет. При этом признак Коши несколько
чувствительнее, чем признак Даламбера.
Это видно из следующего примера:
–
нет. При этом признак Коши несколько
чувствительнее, чем признак Даламбера.
Это видно из следующего примера:
Рассмотрим ряд
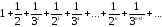 ,
т.е. общий член этого ряда
,
т.е. общий член этого ряда .
Отсюда
.
Отсюда

Таким образом,
отношение
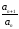 все время «перескакивает» через единицу,
и признак Даламбера здесь не применим.
Вместе с тем признак Коши дает нам
все время «перескакивает» через единицу,
и признак Даламбера здесь не применим.
Вместе с тем признак Коши дает нам ,
и
,
и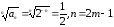 тем самым указывает на сходимость ряда.
тем самым указывает на сходимость ряда.
Пример 11. Исследовать
сходимость ряда
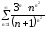 .
.
Применим признак Коши к общему члену ряда и воспользуемся 2 замечательным пределом:
 .
Ряд расходится.
.
Ряд расходится.
ПРИМЕР 12. Исследовать на сходимость ряды
 .
.
Применяя признак Коши, получим
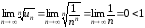 .
.
Следовательно, ряд сходится.
Пример 13. Исследовать
сходимость ряда
 .
.
Так как
 ,
то ряд сходится.
,
то ряд сходится.
Теорема 2.7.
(Обобщенный признак Коши).
Если существует верхний предел
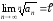 ,
то при
,
то при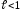 ряд сходится, а при
ряд сходится, а при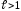 ряд расходится.
ряд расходится.
Пример 14. Исследуем
на сходимость ряд
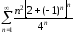 .
.
Первая мысль при
рассмотрении данного ряда, – применить
признаки Коши и Даламбера. Но оба предела
 и
и не существуют. Однако верхний предел
не существуют. Однако верхний предел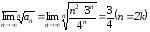 существует и меньше единицы. По общему
признаку Коши, данный ряд сходится.
существует и меньше единицы. По общему
признаку Коши, данный ряд сходится.
Напомним читателю,
что из любой ограниченной последовательности
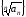 можно выделить сходящуюся
подпоследовательность, предел которой
называется частичным пределом. Таких
подпоследовательностей может быть
несколько. Наибольшей частичный предел
(он всегда существует в случае ограниченной
последовательности) называетсяверхним
пределом
данной последовательности. В частности,
в данном примере из подпоследовательности
можно выделить сходящуюся
подпоследовательность, предел которой
называется частичным пределом. Таких
подпоследовательностей может быть
несколько. Наибольшей частичный предел
(он всегда существует в случае ограниченной
последовательности) называетсяверхним
пределом
данной последовательности. В частности,
в данном примере из подпоследовательности
 можно выделить подпоследовательность
можно выделить подпоследовательность ;
её предел будет верхним.
;
её предел будет верхним.
Замечание.В обеих теоремах случай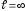 включается в
включается в .
.
Замечание.Если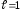 ,
то ряд может сходится, а может расходится.
Поэтому признаки Коши и Даламбера не
подходят и необходимо использовать
другие признаки.
,
то ряд может сходится, а может расходится.
Поэтому признаки Коши и Даламбера не
подходят и необходимо использовать
другие признаки.
Пример. 14. Рассмотрим
гармонический ряд
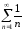 .
Известно, что он расходится. Покажем,
что
.
Известно, что он расходится. Покажем,
что .
Рассмотрим
.
Рассмотрим

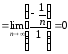
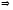
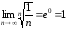 .
.
Пример. 15. Рассмотрим
ряд
 .
.
Выяснить сходимость
этого ряда признаком Даламбера не
удается, так как
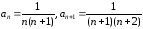 и
и
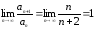 .
.
Найдем сумму ряда по определению. Заметим, что
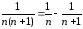 .
.
Тогда исходный ряд можно записать в виде:
 .
.
Частичная сумма
первых
 членов после раскрытия скобок и сокращения
будет равна
членов после раскрытия скобок и сокращения
будет равна .
Следовательно,
.
Следовательно,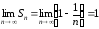 ,
то есть ряд сходится.
,
то есть ряд сходится.
Пример 16. Рассмотрим
ряд
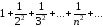 .
.
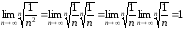 .
.
Этот
ряд сходится, так как
 ,
а ряд
,
а ряд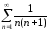 сходится из примера 15, значит ряд тоже
сходится по первому признаку сравнения
сходится из примера 15, значит ряд тоже
сходится по первому признаку сравнения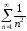 .
.
И наконец, сформулируем еще один признак сходимости, который связывает сходимость ряда со сходимостью некоторого несобственного интеграла.
Теорема 2.8.
(Интегральный признак Коши).
Пусть
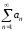 – знакоположительный ряд,
– знакоположительный ряд,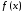 – непрерывная, неотрицательная, монотонно
убывающая на некотором промежутке
– непрерывная, неотрицательная, монотонно
убывающая на некотором промежутке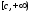 (где
(где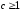 )
функция, такая, что
)
функция, такая, что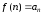 (для любого
(для любого ).
Тогда несобственный интеграл
).
Тогда несобственный интеграл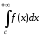 и ряд
и ряд ведут себя одинаково относительно
сходимости.
ведут себя одинаково относительно
сходимости.
Доказательство.
Изобразим члены
ряда геометрически, откладывая по оси
абсцисс номера
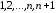 членов ряда, а по оси ординат –
соответственно значения
членов ряда, а по оси ординат –
соответственно значения членов ряда. Построим на том же чертеже
график невозрастающей функции
членов ряда. Построим на том же чертеже
график невозрастающей функции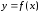 ,
удовлетворяющей условиям
,
удовлетворяющей условиям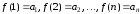 .
Получим, что площадь любого прямоугольника
.
Получим, что площадь любого прямоугольника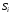 равна
равна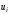 ,
и следовательно,
,
и следовательно, – частичная сумма ряда равна сумме
площадей построенных прямоугольников.
Рассмотрим ступенчатую фигуру,
образованную этими прямоугольниками.
Она закрывает область, ограниченную
кривой
– частичная сумма ряда равна сумме
площадей построенных прямоугольников.
Рассмотрим ступенчатую фигуру,
образованную этими прямоугольниками.
Она закрывает область, ограниченную
кривой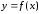 и прямыми
и прямыми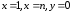 .
Площадь этой области равна
.
Площадь этой области равна .
Следовательно,
.
Следовательно, .
.
Рассмотрим теперь
Рис. 2. Здесь первый слева из прямоугольников
имеет высоту
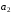 ,
второй
,
второй и т.д. Площадь последнего из построенных
прямоугольников равна
и т.д. Площадь последнего из построенных
прямоугольников равна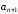 .
Следовательно, площадь всех построенных
прямоугольников равна сумме всех членов
ряда, начиная от второго до
.
Следовательно, площадь всех построенных
прямоугольников равна сумме всех членов
ряда, начиная от второго до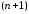 –го,
то есть
–го,
то есть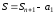 .
С другой стороны, ступенчатая фигура,
образованная этими прямоугольниками
содержится внутри кривой фигуры,
ограниченной кривой
.
С другой стороны, ступенчатая фигура,
образованная этими прямоугольниками
содержится внутри кривой фигуры,
ограниченной кривой и прямыми
и прямыми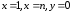 .
Получаем
.
Получаем
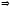
 .
.
Рассмотрим два случая:
Интеграл
 – сходится,
то есть имеет конечное значение, так
как
– сходится,
то есть имеет конечное значение, так
как

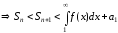 .
.
Так как сумма
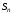 – ограниченна,
и при любых
– ограниченна,
и при любых
 ,
при
,
при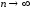 возрастает (учитывая, что
возрастает (учитывая, что )
то, существует
)
то, существует и тогда по определению сходящегося
ряда, ряд сходится.
и тогда по определению сходящегося
ряда, ряд сходится.
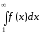 –расходится. Это
означает, что
–расходится. Это
означает, что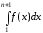 неограниченно
возрастает при
неограниченно
возрастает при
 и тогда, в силу неравенства
и тогда, в силу неравенства ,
, – неограниченно
возрастает при возрастании
– неограниченно
возрастает при возрастании
 .
Значит ряд расходится. Теорема доказана.
.
Значит ряд расходится. Теорема доказана.
Замечания.
Признак основан на сравнении рядов с несобственными интегралами.
Функцию
 ,
принимающую в точках
,
принимающую в точках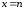 значения
значения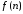 ,
чаще всего удается построить с помощью
замены натурального
,
чаще всего удается построить с помощью
замены натурального в выражении
в выражении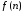 ,
чаще на непрерывно изменяющийся аргумент
,
чаще на непрерывно изменяющийся аргумент .
Так, например, если
.
Так, например, если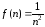 ,
то
,
то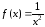 ;
если
;
если ,
то
,
то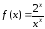 .
Однако, не всегда таким образом можно
получить функцию
.
Однако, не всегда таким образом можно
получить функцию .
Если, например
.
Если, например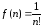 ,
то в этом случае нельзя заменить
,
то в этом случае нельзя заменить на
на ,
так как символ
,
так как символ при нецелых
при нецелых не имеет смысла. Это не означает, что
не существует функции
не имеет смысла. Это не означает, что
не существует функции ,
принимающей в точках
,
принимающей в точках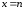 значения
значения .
Напротив, она всегда существует, но ее
аналитическое выражение не всегда
просто найти.
.
Напротив, она всегда существует, но ее
аналитическое выражение не всегда
просто найти.Достоинство интегрального признака Коши состоит в том, что он четко проводит различие между все более медленно сходящимися рядами, даже если члены одного из них лишь незначительно отличаются от членов другого, что иллюстрируется приведенным ниже примером 17.
Интегральный признак Коши применим к рядам, в которых положительные члены монотонно убывают с увеличением их номера. Но даже и для таких функций может оказаться, что путь непосредственного вычисления интеграла при применении интегрального признака сходимости не всегда приемлем. Например, для ряда
 требуется вычислить интеграл
требуется вычислить интеграл ,
что затруднительно. К данному ряду
очевидно применение первого признака
сравнения: при
,
что затруднительно. К данному ряду
очевидно применение первого признака
сравнения: при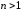 мы имеем
мы имеем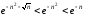 ,
а ряд
,
а ряд сходится как геометрическая прогрессия
со знаменателем
сходится как геометрическая прогрессия
со знаменателем .
.
Пример 17. Исследовать
на сходимость ряд
 (
(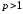 ).
).
Рассмотрим функцию
 .
Эта функция на промежутке
.
Эта функция на промежутке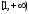 непрерывна, неотрицательна, монотонно
убывает. Кроме того, для любого натурального
непрерывна, неотрицательна, монотонно
убывает. Кроме того, для любого натурального
 .
.
Следовательно,
несобственный интеграл
 и ряд
и ряд ведут себя одинаково относительно
сходимости. Рассмотрим указанный
несобственный интеграл. Имеем
ведут себя одинаково относительно
сходимости. Рассмотрим указанный
несобственный интеграл. Имеем
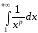
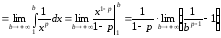 .
.
Так как по условию
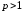 ,
то
,
то .
Но тогда
.
Но тогда при
при и
и
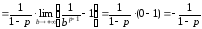 .
.
Итак, получили,
что несобственный интеграл
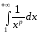 при
при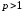 сходится. Следовательно, ряд
сходится. Следовательно, ряд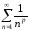 (
( )
тоже сходится.
)
тоже сходится.
Пример 18. Исследуем
сходимость ряда
 интегральным признаком Коши.
интегральным признаком Коши.
По формуле общего
члена введем функцию
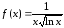 .
Она непрерывна и монотонно убывает на
промежутке
.
Она непрерывна и монотонно убывает на
промежутке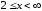 .
Вычислим несобственный интеграл
.
Вычислим несобственный интеграл
 .
.
Интеграл расходится, поэтому расходится и ряд.
При исследовании
сходимости ряда
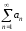 с положительными членами иногда
используется метод выделения главной
части. Он применяется там, где удается
получить с помощью формулы Тейлора
асимптотическую формулу вид
с положительными членами иногда
используется метод выделения главной
части. Он применяется там, где удается
получить с помощью формулы Тейлора
асимптотическую формулу вид .
В этом случае ряд
.
В этом случае ряд сходится или расходится одновременно
с обобщенным гармоническим рядом
сходится или расходится одновременно
с обобщенным гармоническим рядом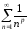 (см пример 17).
(см пример 17).
Пример 18. Исследовать
на сходимость ряд
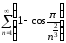 .
.
Так как
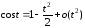 при
при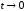 ,
то
,
то
 ,
,
откуда
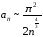 .
Следовательно, ряд
.
Следовательно, ряд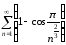 сходится.
сходится.
При оценке
факториалов больших чисел и вычислении
пределов, содержащих
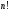 бывает полезна формул Стиглинга:
бывает полезна формул Стиглинга: ,
которая означает, что
,
которая означает, что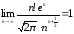 .
.
Пример 19. Исследовать
сходимость ряда
 .
.
Применение признака
Даламбера в данном случае затруднительно.
Используем радикальный признак Коши и
заменим
 по формуле Стирлинга на
по формуле Стирлинга на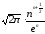 .
.
 .
.
Ряд расходится.