- •Глава Числовые ряды
- •§ 1. Определение числового ряда и основные теоремы
- •§2. Достаточные признаки сходимости знакопостоянных рядов
- •§3.Знакочередующиеся и знакопеременные ряды
- •§4. Некоторые применения теория числовых рядов
- •Степенные ряды.
- •§ 1 Основные определения
- •§ 2. Степенные ряды
- •§ 3 Разложение функций в ряды
- •§ 4. Приложение степенных рядов
- •§ 5. Тригонометрические ряды Фурье
§3.Знакочередующиеся и знакопеременные ряды
Ряд
с членами произвольных знаков называют
знакопеременным. Ряд называют
знакочередующимся, если любые два его
соседних члена имеют противоположные
знаки. Запись знакочередующегося ряда:
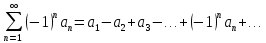 .
.
Определение 1. Знакопеременный ряд называют абсолютно сходящимся, если сходится ряд, составленный из модулей членов исходного ряда.
Замечание.
§4. Некоторые применения теория числовых рядов
Исследование сходимости несобственных интегралов с бесконечными пределами основано на использовании интегрального признака Коши.
Пример 1. Исследовать
на сходимость
 .
.
Функция
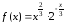 непрерывна и положительна для
непрерывна и положительна для .
Составим ряд
.
Составим ряд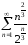 .
Он сходится по признаку Даламбера, так
как
.
Он сходится по признаку Даламбера, так
как
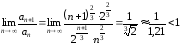 .
.
Из сходимости ряда вытекает сходимость данного интеграла.
Достаточные признаки можно использовать для доказательства равенств вида
 .
.
Пример 2. Доказать,
что
 .
Обозначим
.
Обозначим ,
, .
Составим ряд
.
Составим ряд .
Исследуем его сходимость признаком
Даламбера:
.
Исследуем его сходимость признаком
Даламбера:
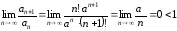 .
.
Так как ряд с общим
членом
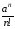 сходится, то
сходится, то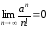 по необходимому признаку сходимости.
по необходимому признаку сходимости.
Степенные ряды.
§ 1 Основные определения
Пусть на некотором множестве
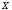 определена
последовательность функций
определена
последовательность функций .
.
Определение 1.1.Функциональным рядом называют алгебраическую сумму членов функциональной последовательности:
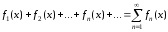 ,
,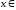 R.
R.
При подстановке в функциональный ряд
фиксированных значений аргумента
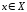 получают различные числовые ряды, среди
которых могут оказаться как сходящиеся,
так и расходящиеся
получают различные числовые ряды, среди
которых могут оказаться как сходящиеся,
так и расходящиеся
Определение 1.2.Множество всех
значений переменной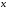 ,
для которых функциональный ряд
,
для которых функциональный ряд сходится, называют областью сходимости
данного ряда.
сходится, называют областью сходимости
данного ряда.
Различают области условной и абсолютной сходимости функционального ряда, как и в случае числовых рядов.
Определение 1.3.Функциональный ряд называют абсолютно сходящимся на
множестве
называют абсолютно сходящимся на
множестве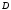 ,
если на этом множестве сходится ряд из
модулей данного ряда
,
если на этом множестве сходится ряд из
модулей данного ряда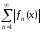 .
.
Для определения области сходимости
ряда
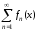 следует решить одно из функциональных
неравенств:
следует решить одно из функциональных
неравенств:
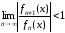 ;
;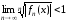 .
.
Вопрос о сходимости функционального ряда на границе области решается исследованием уже числового ряда на сходимость.
Определение 1.4.Ряд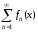 называют сходящимся в точке
называют сходящимся в точке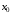 ,
если сходится числовой ряд
,
если сходится числовой ряд .
.
Ряд называют сходящимся на множестве
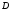 ,
если он сходится в каждой точке этой
области.
,
если он сходится в каждой точке этой
области.
Определение 1.5.Частичной суммой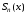 ряда
ряда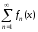 называют сумму
называют сумму первых членов ряда:
первых членов ряда: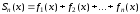 .
Предел частичных сумм ряда, который
сходится на множестве
.
Предел частичных сумм ряда, который
сходится на множестве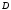 ,
называют его суммой:
,
называют его суммой: или
или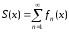 .
При этом говорят, что функция разложена
в ряд по функциям
.
При этом говорят, что функция разложена
в ряд по функциям![]() .
.
Определение 1.6.Сходимость
функционального ряда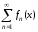 в точке
в точке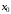 означает, что для любого больше
означает, что для любого больше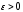 существует такое натуральное число
существует такое натуральное число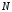 ,
то при всех
,
то при всех выполняется неравенство
выполняется неравенство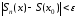 для фиксированного значения
для фиксированного значения .
.
§ 2. Степенные ряды
Определение 2.1.Функциональные ряды
вида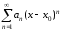 ,
где
,
где R,
называют степенными рядами. Выполним
замену:
R,
называют степенными рядами. Выполним
замену: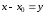 ,
получаем степенной ряд вида
,
получаем степенной ряд вида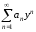 .
Исследование его сходимости эквивалентно
исследованию сходимости ряда
.
Исследование его сходимости эквивалентно
исследованию сходимости ряда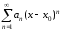 ,
поэтому далее будем исследовать
сходимость ряда
,
поэтому далее будем исследовать
сходимость ряда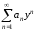 .
.
Определение 2.2.Областью сходимости
степенного ряда называют совокупность
тех значений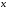 ,
при которых степенной ряд
,
при которых степенной ряд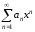 сходится.
сходится.
Геометрически областью сходимости могут служить интервалы замкнутые, открытые, полузакрытые или объединения приведенных интервалов.
Число
 такое, что при
такое, что при ряд
ряд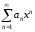 сходится, а при
сходится, а при расходится, называют радиусом сходимости
степенного ряда. Интервал
расходится, называют радиусом сходимости
степенного ряда. Интервал называют
интервалом сходимости. При
называют
интервалом сходимости. При ряд (числовой) может, как сходиться,
так и расходиться.
ряд (числовой) может, как сходиться,
так и расходиться.
Радиус сходимости степенного ряда
 находят по формулам:
находят по формулам:
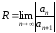 ;
;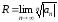 .
.
А интервал сходимости – по формулам:
 (по
признаку Даламбера);
(по
признаку Даламбера);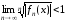 .
.
А затем исследуют поведение ряда на границах интервала.
Теорема 2.3. Радиусы сходимости следующих рядов равны между собой:
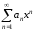 ,
,
 ,
,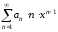 .
.
Теорема
2.4. (Абеля) Если степенной
ряд
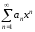 сходится
при
сходится
при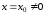 ,
то оно сходится абсолютно длю всех
,
то оно сходится абсолютно длю всех ,
удовлетворяющих неравенству:
,
удовлетворяющих неравенству:
 .
.
Следствие:члены степенного ряда
являются непрерывными функциями, и на
всяком интервале, лежащем внутри
интервала сходимости, сумма ряда является
непрерывной функцией на отрезке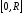 действительной оси.
действительной оси.
Замечание. Все изложенное
переносится и на ряд с помощью замены
с помощью замены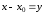 .
.
Теорема 2.5. Пусть – радиус сходимости степенного ряда
– радиус сходимости степенного ряда
|
|
(1) |
Тогда функция
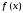 имеет в интервале
имеет в интервале производные всех порядков, и их находят
почленным дифференцированием ряда (1).
Для любых
производные всех порядков, и их находят
почленным дифференцированием ряда (1).
Для любых .
.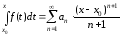
То есть внутри интервала сходимости степенной ряд можно почленно интегрировать.
Замечания:
Степенные ряды, полученные из ряда (1) в результате почленного дифференцирования или интегрирования, имеют тот же радиус сходимости, что и исходный ряд.
Дифференцирование и интегрирование рядов часть используют для нахождения суммы
 ряда. Если легко найти сумму ряда из
производных (или интегралов), то
дифференцируя (или интегрируя) ряд с
известной суммой, находят и сумму
исходного ряда.
ряда. Если легко найти сумму ряда из
производных (или интегралов), то
дифференцируя (или интегрируя) ряд с
известной суммой, находят и сумму
исходного ряда.
При дифференцировании ряда несколько раз для нахождения суммы ряда приходится решать некоторое дифференциальное уравнение по найденной линейной зависимости между суммой исходного ряда и её производными.
Дифференцирование и интегрирование рядов используют и для нахождения сумм числовых рядов. Если сумма
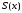 функционального ряда найдена, и ряд
сходится при значении
функционального ряда найдена, и ряд
сходится при значении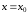 ,
то число
,
то число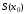 является суммой данного числового
ряда.
является суммой данного числового
ряда.
Пример
1. Найти область сходимости ряда
 .
.
Имеем
степенной ряд. Найдем интервал его
сходимости, используя функциональное
неравенство
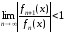 .
.
Выписываем
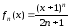 ,
,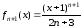 ,
откуда
,
откуда
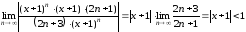
или
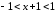 ,
тогда интервал сходимости ряда:
,
тогда интервал сходимости ряда: .
.
Исследуем поведение ряда в граничных точках интервала:
 .
Получаем числовой ряд
.
Получаем числовой ряд
 .
Он знакочередующийся. Ряд из его модулей
.
Он знакочередующийся. Ряд из его модулей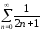 расходится. Поэтому
исходный ряд абсолютно расходящийся.
Исследуем исходный ряд на условную
сходимость. По формуле общего члена
введем функцию непрерывного аргумента
расходится. Поэтому
исходный ряд абсолютно расходящийся.
Исследуем исходный ряд на условную
сходимость. По формуле общего члена
введем функцию непрерывного аргумента
 :
: .
Найдем
.
Найдем ,
функция монотонно убывает для
,
функция монотонно убывает для .
Находим
.
Находим .
Все условия теоремы Лейбница выполнены,
поэтому ряд условно сходится. То есть
левая граница интервала сходимости
точка
.
Все условия теоремы Лейбница выполнены,
поэтому ряд условно сходится. То есть
левая граница интервала сходимости
точка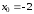 входит в область сходимости исходного
ряда.
входит в область сходимости исходного
ряда. .
Тогда имеем ряд
.
Тогда имеем ряд
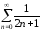 .
Он расходится, то есть правая граничная
точка
.
Он расходится, то есть правая граничная
точка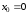 ,
не входит в область сходимости ряда.
Итак, область сходимости исходного
ряда:
,
не входит в область сходимости ряда.
Итак, область сходимости исходного
ряда: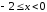 или
или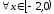 .
.
Пример 2. Найти сумму ряда
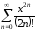 .
.
Обозначим сумму исходного ряда
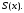 Находим
Находим
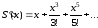 ,
,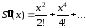 .
.
Замечаем:
 – это однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами и начальными условиями:
– это однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами и начальными условиями: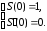
Для нахождения функции
 решаем задачу Коши:
решаем задачу Коши: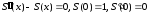 .
.
Решение ищем в виде:
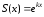 .
Тогда характеристическое уравнение
имеет вид:
.
Тогда характеристическое уравнение
имеет вид: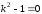
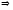
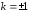
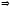
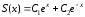 .
Используем начальные условия:
.
Используем начальные условия: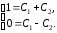
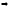
 откуда
откуда .
.
Пример 3. Найти сумму ряда
 .
.
Сделаем замену переменной
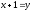 .
Тогда имеем ряд
.
Тогда имеем ряд .
Почленно его интегрируем:
.
Почленно его интегрируем:
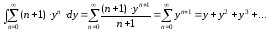 –
–
геометрическая
прогрессия при
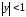 ,
её сумму обозначим через
,
её сумму обозначим через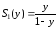 .
Тогда
.
Тогда ,
откуда сумма исходного ряда
,
откуда сумма исходного ряда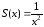 в области
в области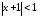 или
или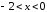 .
.