
- •Глава Числовые ряды
- •§ 1. Определение числового ряда и основные теоремы
- •§2. Достаточные признаки сходимости знакопостоянных рядов
- •§3.Знакочередующиеся и знакопеременные ряды
- •§4. Некоторые применения теория числовых рядов
- •Степенные ряды.
- •§ 1 Основные определения
- •§ 2. Степенные ряды
- •§ 3 Разложение функций в ряды
- •§ 4. Приложение степенных рядов
- •§ 5. Тригонометрические ряды Фурье
Глава Числовые ряды
§ 1. Определение числового ряда и основные теоремы
Определение 1.1:
Последовательностью действительных
чисел называется функция
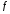 ,
определённая на множестве всех натуральных
чисел. Число
,
определённая на множестве всех натуральных
чисел. Число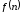 называется
называется -ным
членом последовательности и обозначается
-ным
членом последовательности и обозначается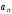 ,
а формула
,
а формула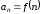 называется формулой общего члена
последовательности.
называется формулой общего члена
последовательности.
Определение 1.2.
Пусть имеется некоторая, составленная
по определённому закону, бесконечная
последовательность чисел
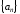 ,
чисто формально соединённых между собой
знаками плюс:
,
чисто формально соединённых между собой
знаками плюс:
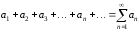 .
(1)
.
(1)
Такое выражение
называется числовым
рядом. Числа
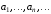 называются членами ряда;
называются членами ряда; -ный
член ряда
-ный
член ряда называется также общим членом ряда. Ряд
(1) считается заданным, если известен
общий член его, выраженный как функция
номера
называется также общим членом ряда. Ряд
(1) считается заданным, если известен
общий член его, выраженный как функция
номера :
: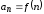 .
.
Укажите числовые ряды среди следующих объектов:
1)
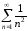 ; 2)
; 2)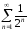 ; 3)
; 3)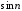 ;
;
4)
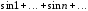 ;
5)
;
5)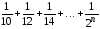 .
.
Определение 1.3:
Ряд
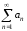 называетсясходящимся,
если последовательность частичных сумм
имеет предел, т.е.
называетсясходящимся,
если последовательность частичных сумм
имеет предел, т.е.
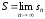
Здесь
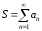 называется
суммой ряда.
называется
суммой ряда.
Если же
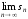 не существует (в частности
не существует (в частности ),
то говорят, чторяд
расходится.
),
то говорят, чторяд
расходится.
Определение 1.4:
Ряд
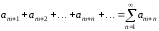 ,
полученный из ряда
,
полученный из ряда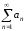 отбрасыванием первых
отбрасыванием первых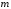 членов, называется
членов, называется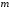 -ным
остатком ряда.
-ным
остатком ряда.
Найти частичные
суммы
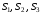 ряда
ряда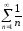 .
.
Справедливы следующие теоремы:
Теорема 1.5: Отбрасывание от ряда или присоединение к ряду любого конечного числа начальных членов не меняет его сходимости или расходимости.
Доказательство:
Для случая, когда
мы отбрасываем из ряда конечное число
его членов. Пусть дан ряд
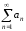 .
Обозначим сумму отброшенных членов
через
.
Обозначим сумму отброшенных членов
через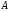 :
: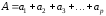 .
Пусть сумма
.
Пусть сумма первых членов ряда равна
первых членов ряда равна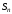 ,
сумма
,
сумма первых членов остатка
первых членов остатка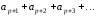 равна
равна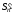 .
Тогда
.
Тогда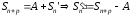 .
Предположим, что ряд сходится, и пусть
.
Предположим, что ряд сходится, и пусть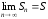 ,
а следовательно и
,
а следовательно и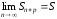 .
В таком случае
.
В таком случае ,
и следовательно , остаток ряда тоже
сходится.
,
и следовательно , остаток ряда тоже
сходится.
Предположим теперь,
что остаток ряда
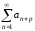 сходится, и пусть
сходится, и пусть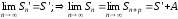 .
.
Поэтому сам ряд тоже сходится. Теорема доказана.
Тем саамы доказано, что из сходимости одного из наших рядов следует и сходимость другого.
Следствие. При исследовании ряда на сходимость можно игнорировать конечное число его членов.
Подумайте и скажите, на что влияет процедура отбрасывания первых членов ряда?
Теорема 1.6: Если
ряд
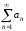 – сходится, то предел его
– сходится, то предел его -го
остатка при
-го
остатка при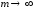 равен нулю.
равен нулю.
Доказательство:
Обозначим остаток
ряда через
 ,
а сумму всего ряда через –
,
а сумму всего ряда через –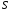 . Тогда
. Тогда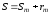 .
Так как ряд сходится, то
.
Так как ряд сходится, то
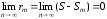 .
.
Теорема доказана.
Что Вы скажете о
сходимости ряда, если известно, что
предел
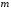 -го
остатка ряда не равен нулю?
-го
остатка ряда не равен нулю?
Теорема 1.7:
Умножение
членов сходящегося ряда на любое число
 не нарушает его сходимости.
не нарушает его сходимости.
Подумайте, чему
будет равна сумма ряда
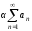 ?
?
Верно ли утверждение:
если члены расходящегося ряда умножить
на число
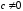 ,
то вновь получится расходящийся ряд.
,
то вновь получится расходящийся ряд.
Теорема 1.8: Если
ряды
 и
и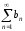 – сходятся и имеют соответственно суммы
– сходятся и имеют соответственно суммы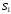 и
и ,
то сходится и ряд
,
то сходится и ряд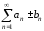 ,
причём его сумма равна
,
причём его сумма равна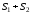 .
.
Ряд
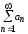 ,
составленный из отрицательных членов,
сходится. Ряд
,
составленный из отрицательных членов,
сходится. Ряд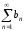 ,
составленный из положительных членов,
расходится. Сходится или расходится
ряд
,
составленный из положительных членов,
расходится. Сходится или расходится
ряд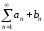 ?
?Дан ряд
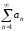 .
Оказалось, что ряд
.
Оказалось, что ряд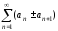 сходится. Следует ли отсюда, что ряд
сходится. Следует ли отсюда, что ряд сходится?
сходится?
Одна из важнейших задач теории числовых рядов – вычисление их сумм. Как правило, эта задача вызывает затруднения, но в некоторых случаях сумма ряда находится достаточно просто. Приведём пример такого рода.
Пример 1. Дан ряд
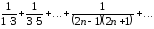 .
Доказать его сходимость, пользуясь
определением; найти сумму ряда.
.
Доказать его сходимость, пользуясь
определением; найти сумму ряда.
Решение:
Общий член ряда
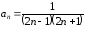 можно представить в виде:
можно представить в виде:
 ,
,
Где коэффициенты
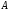 и
и можно найти методом неопределённых
коэффициентов:
можно найти методом неопределённых
коэффициентов:
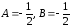 ,
т.е.
,
т.е.
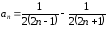 .
.
Найдём частичную
сумму:
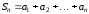
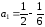 ,
,
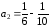 ,
,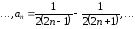 .
.
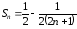 .
.
Откуда по определению
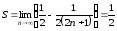 .
.
Таким образом, ряд сходится.
Пример 2. Рассмотрим ряд, представляющий собой сумму членов геометрической прогрессии:
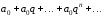 .
.
Исследуем сходимость
данного ряда. Для этого рассмотрим его
частичную сумму
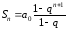 .
Найдём её предел:
.
Найдём её предел: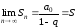 ,
если
,
если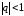 .
.
Следовательно,
ряд
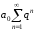 при
при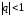 сходится. Если
сходится. Если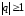 ,
то
,
то ,
т.е. ряд расходится.
,
т.е. ряд расходится.
Дан ряд
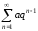 ,
сходится или расходится он при
,
сходится или расходится он при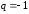 ?
?
Обычно, прежде чем браться за вычисление суммы ряда, нужно выяснить, сходится или расходится данный ряд, т.к. расходящийся ряд суммы не имеет. При этом особое значение приобретает задача об исследовании ряда на сходимость. Приведём теоремы, выражающие общие признаки сходимости числовых рядов. Начнём с необходимого признака сходимости ряда.
Теорема 1.9: Если
ряд
 сходится, то
сходится, то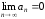 .
.
Доказательство:
По условию ряд
 сходится. Обозначим его сумму
сходится. Обозначим его сумму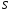 .
Рассмотрим две частичные суммы ряда:
.
Рассмотрим две частичные суммы ряда: и
и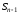 .
.
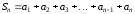 ,
,
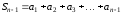 .
.
Разность
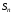 и
и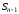 даёт общий член ряда
даёт общий член ряда .
По определению суммы ряда:
.
По определению суммы ряда:
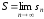 ,
, ,
откуда
,
откуда
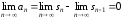 .
.
Следствие теоремы
1.5. (достаточный
признак расходимости ряда):
Если
 не равен нулю или не существует, то ряд
не равен нулю или не существует, то ряд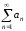 расходится.
расходится.
Замечание:
Убывание слагаемых ещё не достаточно для сходимости ряда. Так геометрический ряд
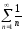 расходится, хотя
расходится, хотя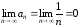 .
.Если
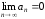 ,
то есть смысл исследовать ряд на
сходимость дальше.
,
то есть смысл исследовать ряд на
сходимость дальше.
