2 Вывод формулы для пошагового вычисления

УГЛОВОЙ СКОРОСТИ ЗВЕНА ПРИВЕДЕНИЯ

Рассмотрим только установившееся движение, при котором скорости звеньев и кинематическая энергия машины периодически изменя­ются. В начале и в конце каждого цикла они имеют одинаковые значения. Время цикла равно времени одного оборота кривошипа: периоду изменения производственного сопротивления.

Заданы номинальная n_Дв= 2880 об/мин и синхроннаяп_сх = 3000 об/мин частоты вращения ротора асинхронного электродвигателя; массы, моменты инерции и размеры звеньев; диаграмма изменения производственного сопротивления. Момент двигателя на рабочем участке его механической характеристики линейно зависит от частоты вращения (угловой скорости).

Требуется найти зависимость угловой скорости звена приведения от координаты , определяющей его положение; в случае необходимости определить момент инерции маховика; определить приближенное значение мощности, развиваемой двигателем без учета потерь на трение.

Звенья механизмов считаем абсолютно твердыми телами, зазорами в кинематических парах пренебрегаем. Тогда машинный агрегат можно считать машиной, число степеней свободы которой равно единице и для которой можно записать дифференциальное уравнение движения:

, (10)

где – приведенный момент инерции машины;– приведенный момент движущих сил и модуль приведенного момента сил сопротивления;– угол поворота и угловая скорость звена приведения.

Преобразуем уравнение, умножив все слагаемые на :

. (10,а)

Независимой переменной в этом уравнении является координата . Её бесконечно малое приращениепри численном интегрировании уравнения заменим малым конечным изменением– шагом интегрирования.

Переменные конечные величины в уравнении (10,а) на каждомi-ом шаге вычислений будем считать постоянными и равными их значениям в начале шага:

.

Бесконечно малые приращения dI_пр изаменим малыми разностями, соответствующими изменению:

.

Индекс показывает, что данная величина определяется в начале следующего шага.

После всех этих замен выразим значение угловой скорости в начале следующего шага

. (11)

Формула (11) используется для пошагового вычисления угловой скорости. В качестве начального звена машины выберем кривошип 1 рычажного механизма. Шаг изменения угла поворота кривошипа . Для вычисления необходимо найти значения. Скоростьопределена на предыдущем шаге расчётов.

3 Определение приведенного момента инерции

Приведенный момент инерции машины определяется по формуле

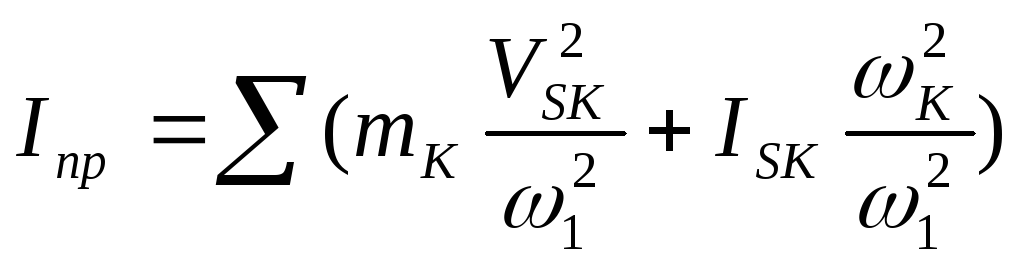, (12)

где m_K,V_SK– масса и скорость центра масск-того звена;I_SK,– момент инерции относительно оси, проходящей через центр масс, и угловая скорость звена;– угловая скорость кривошипа.

Величину I_np, будем искать как сумму приведенных моментов инерции зубчатого и рычажного механизмов. Приведенный момент инерции зубчатого механизма определяется по формуле

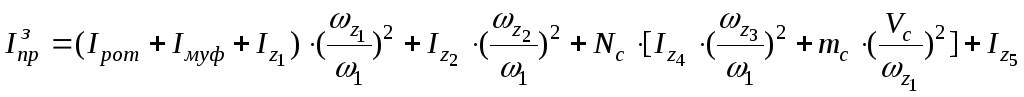(13)

Скорости звеньев редуктора при заданной номинальной частоте вращения двигателяn_Двопределены в пункте 1 пояснительной записки. Подставляя в формулу (13) значения, находим

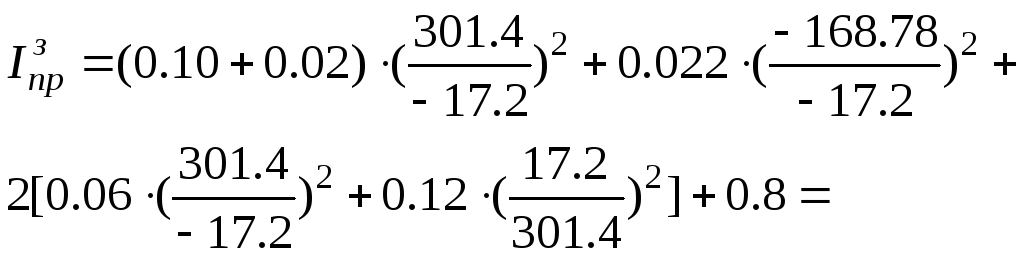
Отношения скоростей звеньев зубчатого механизма не зависят ни от положения, ни от величины скоростей, поэтому приведенный момент является величиной постоянной.

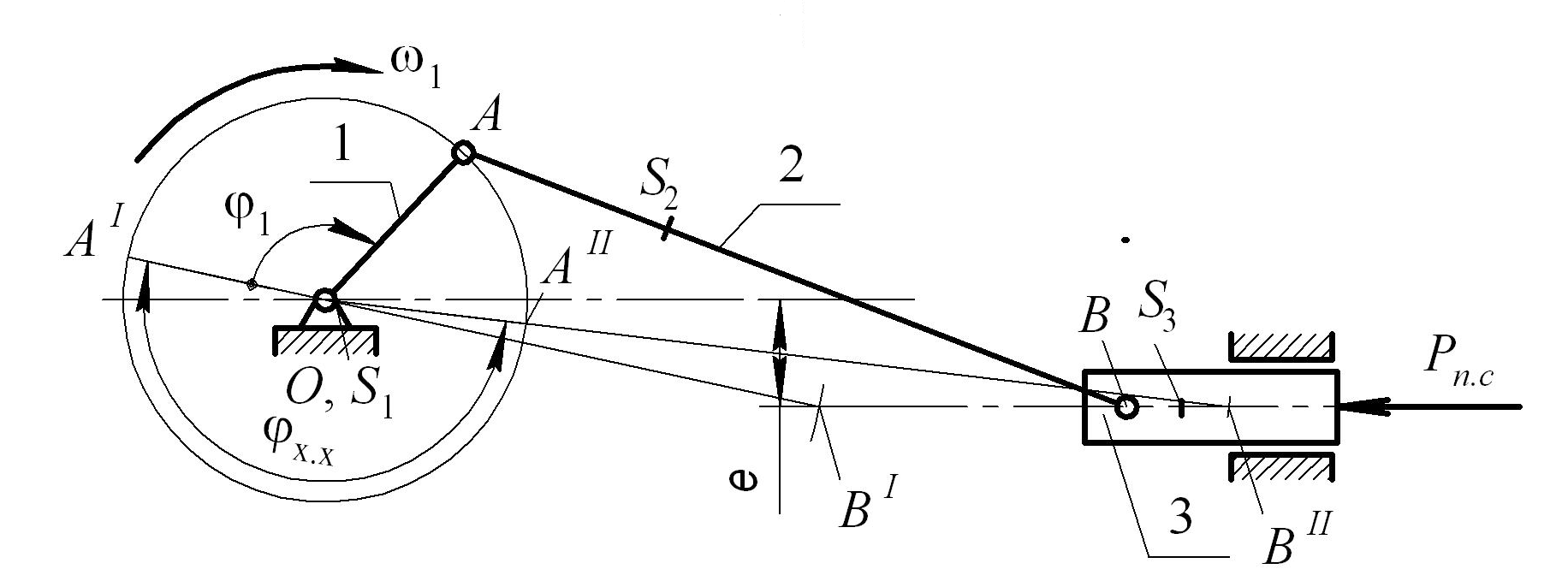
Рисунок 2 – Схема рычажного механизма

Приведенный момент инерции рычажного механизма определяется по формуле:

(14)

В рычажном механизме отношения скоростей звеньев изменяются от положения к положению. Поэтому момент – величина переменная, зависит от угла поворота кривошипа, однако не зависит от величины скоростей.

Отношения скоростей точек и звеньев рычажного механизма на каждом шаге изменения угла поворота кривошипа определяются по результатам кинематического исследования на компьютере. Поэтому для вычисленияв компьютер достаточно ввести массы, моменты инерции и размеры звеньев.