2. Общие положения по работе вибрационных бункерно - загрузочных устройств

Вибрационные бункера предназначены для захвата деталей из навала, ориентации их и последующей выдачи в ориентированном положении в питатель.

Вибрационные бункера являются устройствами с непрерывной выдачей деталей, однако принцип действия их весьма своеобразен. Лоток вибрационного бункерного ориентирующего устройства наклонен под углом к горизонту (рис. 10) и получает возвратно-поступательное перемещение с небольшой амплитудой и значительной частотой в направлении под углом  к лотку.

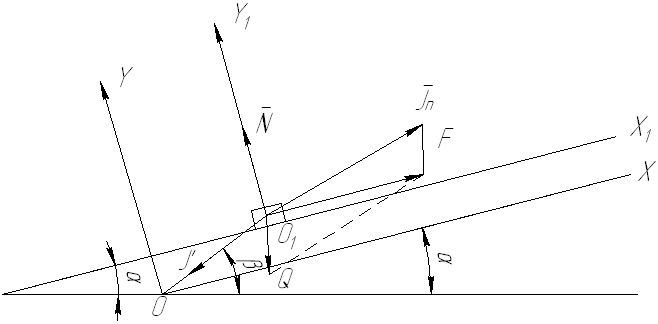
Рис. 10. Геометрические параметры рабочего лотка вибробункера

Если поступательное движение лотка медленное, а возвратное – быстрое, то деталь, лежащая на лотке будет двигаться только наступательно. Так как перемещение детали происходит под действием силы трения, которая не может быть больше, чем то наибольшее ускорение детали(т.н. критическое) будет определять характер движения детали.

Если ускорение лотка будет больше критического, то произойдет проскальзывание деталей по лотку в направлении, обратном движению лотка.

Так как для движения детали вперед, ей необходимо сообщить колебательное движение с разными ускорениями в прямом и обратном направлениях, то в случае хода лотка вперед, ускорение будет меньше , т.е.< и деталь будет двигаться вместе с лотком без проскальзывания, в случае хода лотка назад при >, будет происходить скольжение детали по лотку вперед.

Критическое ускорение, превышение которого будет создавать скольжение детали относительно лотка назад – вниз, при этом равно:

(1)

а критическое ускорение, превышение которого будет создавать скольжение детали относительно лотка вперед-вверх, равно:

(2)

где g – ускорение силы тяжести

f – коэффициент трения заготовки по лотку.

Для вибробункеров с диаметром чаши до 100 мм значения коэффициента f приведены в табл. 3, при диаметре чаши более 100 мм значение коэффициента f необходимо принимать из табл. 2.

При движении лотка вверх сила инерции детали будет действовать противоположно направлению движения и прижимать деталь к лотку, увеличивая силу трения, под действием которой движется деталь. При ходе лотка вниз сила инерции будет уменьшать давление детали на лоток и тем самым уменьшать силу трения, создавая условия для скольжения детали по лотку вперед. В зависимости от ускорения лотка и углов имогут существовать различные режимы движения деталей, как отрывные, при которых деталь – часть каждого цикла – следует не касаясь поверхности транспортирующего лотка, так и безотрывные, при которых деталь все время находится в контакте с поверхностью лотка.

Наиболее эффективными режимами работы вибрационного бункера, позволяющими получить высокие скорости движения при высоких КПД и сохранении большой стабильности движения деталей, являются отрывные режимы.

Основными условиями, определяющими движение детали, являются углы наклона лотка и направляющие вибраций, скорость и ускорение лотка, а также коэффициент трения скольжения f между деталью и лотком.

Примем две системы ориентировки, т.е. осей координат: Первая ХОУ – реновал (по станине бункера), связанная с землей, вторая ХОУ- относительная, связанная с движущимся лотком (рис. 10)

При рассмотрении движения детали по лотку, наклоненному под углом к коризонту и совершающему гармонические колебания под углом(при>), уравнение движения лотка относительно системы ХОУ имеет вид:

= cos (3)

= (4)

= cos (5)

= (6)

где А- размах колебаний лотка в параллельном ему направлении

А- размах колебаний в направлении, перпендикулярном скорости лотка

W – угловая частота колебаний

=Wt – фазовый угол

t – время

Дифференциальное уравнение движения детали и начальный период относительно лотка в системе координат ХОУсвязанной с лотком, имеет вид:

(7)

(8)

где m – масса детали

g – ускорение силы тяжести

N – нормальная реакция

F – сила трения

Процесс движения детали в режимах с отрывом ее от лотка в общем случаю можно рассматривать в пяти этапах. В первом этапе (этап разгона) деталь находится на плоскости лотка (). Уравнение движения детали на первом этапе имеет вид:

(9)

а уравнение абсолютного движения (т.е. относительно неподвижной системы координат) будет иметь вид:

(10)

(11)

(при =0, С=0)

Так как лоток совершает гармонические колебания, то графически первый этап можно представить в виде кривой (рис. 11), физический смысл этого участка кривой состоит в том, что деталь проскальзывает относительно лотка и двигается с ускорением которое определяется по формуле (10). Скорость движения детали растет по кривой, выраженной уравнением (11), пока в точкескорости детали и лотка не сравняются.

В этот момент наступает второй этап, который носит название этапа ПЕРВОГО ТОРМОЖЕНИЯ. Деталь начинает двигаться с замедлением по замедляющему ход лотку (кривая ), но быстрее него.

Уравнение движения детали на этапе торможения имеет вид:

(12)

(13)

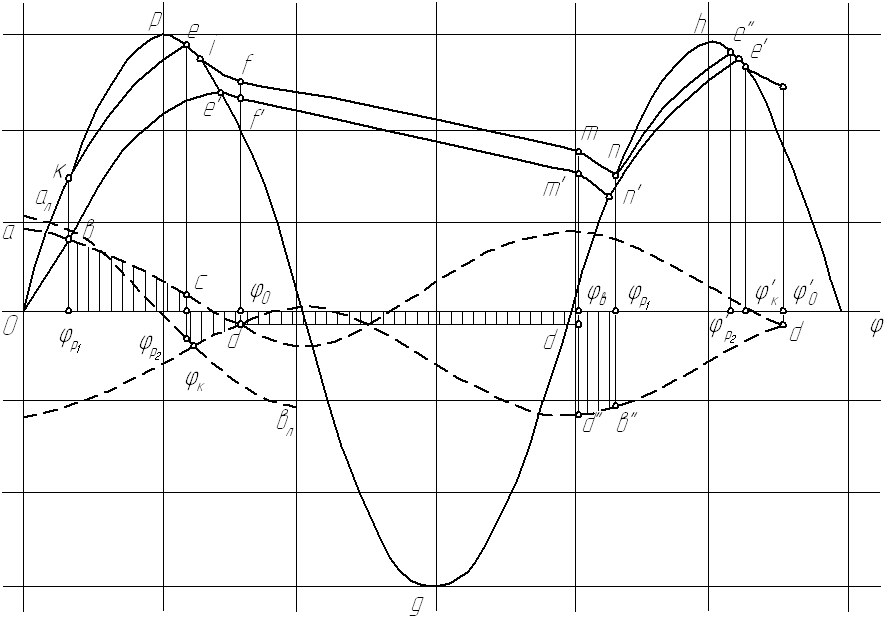
Рис. 11. Графики движения перемещаемой на лотке вибробункера детали

Во второй четверти периода движения ускорение лотка (кривая ) станет отрицательным и сила инерции детали(рис. 10) будет направлена вверх, и, в тот момент, когда нормальная реакцияN станет равной нулю, произойдет отрыв заготовки от лотка.

Фазовый угол, при котором начинается отрыв заготовки от лотка равен

(14)

Режим движения детали, время ее отрыва и время падения на лоток зависит от величины амплитуды нормального ускорения лотка , которую удобно задавать обобщенным безразмерным параметром

(15)

(16)

С момента отрыва детали от лотка начинается третий этап движения – МИКРОПОЛЕТ ДЕТАЛИ в воздухе со скоростью, определяемой кривой . Абсолютное ускорение движения детали вдоль оси Х, если пренебречь сопротивлением воздуха, равно:

(17)

(18)

После микрополета, длительность которого зависит от режима работы лотка, определяемого величиной параметра , деталь падает на лоток и начинается четвертый этап ее движения (этап ВТОРОГО ТОРМОЖЕНИЯ). Точкаотвечает фазовому углу встречи детали с лотком, величина которого может быть определена по следующей формуле:

(19)

При эффективных режимах работы вибробункера скорость детали в момент встречи с лотком (при условии, что удар детали о лоток неупругий) будет больше скорости последнего, поэтому на протяжении четвертого этапа деталь будет двигаться с отрицательным ускорением , которое определяется по формуле (12, 13) пока скорости детали и лотка не сравняются. Такое уравнение скоростей произойдет в момент времени, соответствующий точке.

Далее начинается цикл, в котором деталь будет проскальзывать относительно лотка и скорость движения ее будет расти по кривой (этап разгона), в точкескорости детали и лотка сравняются, последуют остальные три этапа, движения следующего периода.

Как видно из графика, в результате первого колебания деталь приобретает скорость, определяемую точкой , при втором колебании деталь разгоняется до несколько большей скорости (скорость в точкевыше, чем в точке).

В течение нескольких последних колебаний нарастание скорости детали будет продолжаться, пока не наступит режим установившегося движения (кривая ).

Последний наступит тогда, когда прирощение скорости на участке разгона будет равно сумме падения скоростей на участках замедления. Поскольку скорость – интеграл ускорения по времени, а вычисляется интеграл как площадь, то усилие установившегося характера движения детали можно записать:

площадь = площадь(20)

+ площадь + площадь

По выполнению этого условия ордината точки K начала разгона в любом предыдущем цикле будет равна ординате точки n начала разгона в любом следующем цикле. Скорость детали в установившемся режиме в течение цикла будет изменяться по кривой kelfmn и колебаться от (в точкеl) до (в точкеn). При определенных условиях помимо рассмотренных четырех этапов движения возникает пятый ll СОВМЕСТНОГО ДВИЖЕНИЯ ДЕТАЛИ С ЛОТКОМ без проскальзывания.

Такой этап может возникнуть или в конце участка разгона или в его начале, если в эти моменты ускорение лотка будет меньше критического. Наступление этого условия можно записать в общем виде, рассматривая сумму проекций всех сил ось(рис. 10).

(21)

В формуле (21) знак «плюс» для участка разгона детали, а знак «минус» - для участка торможения.