3.8 Определение угла наклона подвесок.

Угол наклона подвесок по вертикали (рис.20) должен обеспечить получение требуемого угла бросанияна спиральном лотке питателя. От правильного определения величины углабудет зависеть режим работы питателя и достигаемая им производительность.

В бункерных вибрационных питателях наклонные подвески обычно располагают таким образом, чтобы горизонтальная проекция их была касательно к окружности радиуса , проходящей черезточки крепления подвесок к чаше. Угол бросания на среднем радиусе спирального лоткаопределяется по формуле:

; (60)

где - кинематический угол наклона подвесок, отличиющийся от статического на величину коэффициента.

; (61)

Для питателей с вертикальным вибратором и подвеской чаши на цилиндрических стержнях, работающих на частоте 50 Гц. в углах:

В двухмассовых конструкциях бункерных вибропитателей углы бросания будут зависеть от динамических параметров системы-соотношения верхней и нижней масс и их моментов инерции. Угол наклона подвесок подсчитывается по формуле:

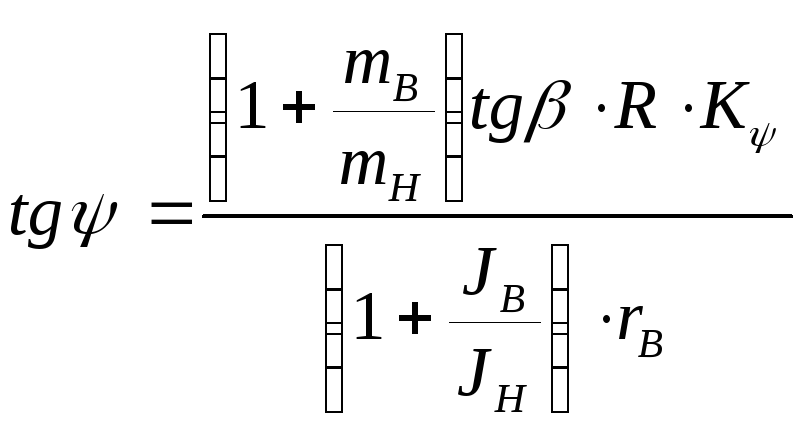; (62)

3.9 Расчет упругой системы вибропитателя.

а). Определение приведенной массы питателя.

Подвижная часть питателя укреплена на трех наклонных пружинных подвесках и масса ее распределения по определенной поверхности. Для того, чтобы определить жесткость подвесок, необходимо подвижную массу питателя привести к точкам крепления подвесок.

Верхняя масса питателя, приведенная к точкам крепления подвесок, подсчитывается:

(68)

где суммарная масса верхней части питателя

- момент инерции верхней части питателя

- расстояние от центра чаши до точек крепления подвесок к верхней части питателя.

- расстояние от оси чаши до точек крепления подвесок в нижней части питателя (рис.20)

Аналогично подсчитывается приведенная масса нижней части питателя.

(64)

Основание питателя обычно устанавливают на пружинных амортизаторах, в результате чего система становится двухмассовой. Приведенную массу для обеих масс можно определить из уравнения:

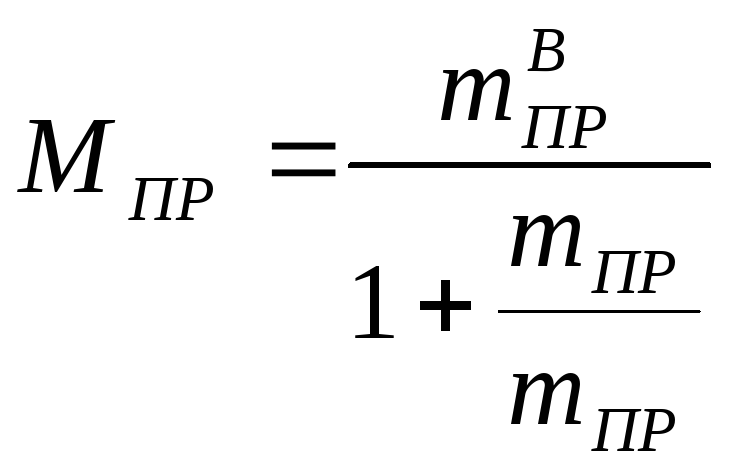; (65)

Установлено, что амплитуда колебаний обратно пропорциональна величине масс. Так как верхняя масса, включающая чашу питателя, является рабочей, то у нее желательно иметь большую амплитуду колебаний. Нижняя – реактивная масса питателя опирается на амортизаторы, и чем меньше амплитуда ее колебаний, тем меньше будет передаваемая вибрация окружающей среде. Поэтому нижнюю массу бункерного вибропитателя обычно выполняют в 2-5 раза большей верхней, т.е.

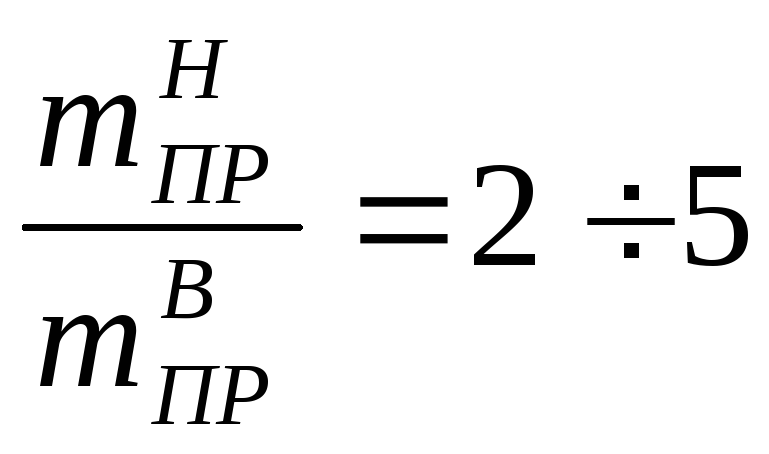; (65а)

3.10. Расчет пружинных подвесок питателя.

Жесткость пружинных подвесок в зависимости от требуемой собственной частоты колебаний системы и приведенной массы определяется по формуле:

; (66)

где число подвесок в питателе ( может быть принято равным 3 или 4).

Жесткость пружинной подвески зависит от ее длины , способа крепления, момента инерции поперечного сеченияи ее материала. Для подвески с двумя защепленными концами жесткость выражается формулой:

; (67)

где

- модуль упругости материала подвески

;

При , необходимый момент инерции сечения подвески равен:

; (68)

Момент инерции цилиндрической пружины можно выразить также:

; (69)

отсюда, сравнив уравнения (68) и (69), получим

; (70)

где

;

частота вибратора

длина пружинного стержня между башмаками закрепления (рис.20)

Момент инерции прямоугольного стержня:

; (71)

где ;

Подставив (71) в (68):

; (72)

длина части пружинного стержня между башмаками крепления (рис.20)

Минимальная длина пружинного стержня определяется из условия, что максимальное напряжение, возникающее в стежне, не превышает допускаемое напряжение на выносливость.

Максимальный изгибающий момент при жестком креплении стержней будет:

; (73)

где

y – прогиб стержня.

Максимальное напряжение в стержне

;

где

момент сопротивления пружинного стержня

Для прямоугольного сечения:

; (74)

где (75)

для круглого сечения:

; (76)

Из условия прочности на выносливость

получим:

(77)

Подставив в формулу (76) значения М и W, получим:

для прямоугольного сечения:

; (78)

т.к. из формулы (71) , то

подставив его значение в формулу (78), получим:

(79)

Преобразовав формулу (79), получим:

; (80)

Решая совместно уравнения (72) и (80), получим формулу для определения минимальной длины пружинного стержня :

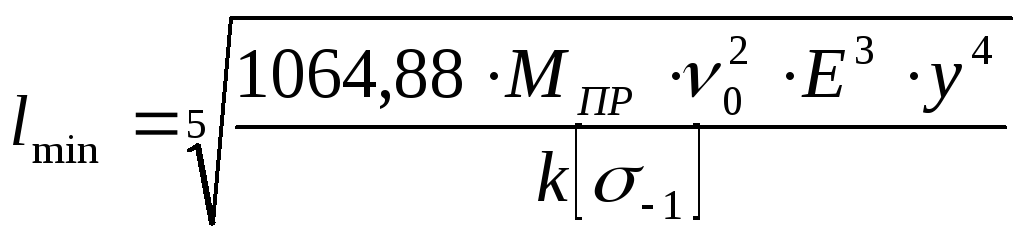; (81)

Если принять среднее значение для пружинных сталей

, то для частоты 50 Гц.

; (82)

для частоты 100 Гц.

; (83)

где - приведенная масса питателя в

- прогиб стержня в см

для круглого сечения.

; (84)

откуда

; (85)