заданным темпом, определяемым соотношением − U0 / Tзи , при этом РС формирует заданную величину отрицательного динамического тока, при
котором |
в |
якорной |
цепи |
будет |
протекать |
|
ток: |
|
Ia уст = −Ia дин + Iс = −1,2Iн + 0,5Iн = −0,7Iн . При сбр |
осе |
нагрузки |
||||||
( Iс = 0) электродвигатель не может тормозиться с заданным темпом, т.к. |
||||||||
Ia уст = −0,7Iн |
< −Ia дин , поэтому отклонение |
напряжения |
uос |
от |
||||
заданного темпа приводит к появлению отрицательной ошибки ∆uc |
< 0 |
|||||||
на входе |
РС |
и увеличению |
величины |
якорного тока |
до |
значения |
||
Ia уст = −Ia дин = −1,2Iн , обеспечивающего заданный темп торможения. После того, как uзс станет равным нулю, на входе РС будет присутствовать только напряжение uос , формируя положительную
ошибку регулирования скорости ∆uc > 0 , за счет которой РС снижает ток в якорной цепи до нуля.
Таким образом, включение ЗИ на входе РС формирует заданный темп изменения скорости (заданное ускорение электродвигателя) во всех режимах работы электропривода, при условии, что РС не заходит в ограничение.
5.5. Учет дополнительных ограничений в структурах подчиненного регулирования
Рассмотренные выше принципы и устройства обеспечивают ограничение непосредственно тех переменных, для которых предусмотрены локальные системы регулирования (тока, скорости и т.д.) со своими регуляторами. Однако реально требуется ограничение и ряда других, дополнительных переменных, для которых специальные контуры регулирования не предусмотрены. Одной из таких величин, требующих ограничения на допустимом уровне, является производная якорного тока по времени (темп изменения якорного тока) [7,8,9,12].
Ограничение темпа изменения якорного тока необходимо для обеспечения без искровой коммутации машин постоянного тока. Для большинства электрических машин постоянного тока относительный допустимый темп изменения якорного тока лежит в пределах 15 … 50 1/с (т.е. 15 … 50 номинальных значений тока в секунду). Следовательно, максимальный темп изменения якорного тока не должен превышать допустимый темп для данного типа машины. Поэтому при проектировании системы регулирования должно быть обеспечено следующее условие:
225
di* |
|
|
≤ |
di* |
, |
(5.60) |
a |
|
|
a |
|||
dt |
|
max |
|
dt |
доп |
|
|
|
|
|
где i*a = ia / Iн - относительное значение якорного тока.
Оценим величину производной якорного тока, которая получается в настроенном на модульный оптимум контуре регулирования якорного тока. Реакция на скачкообразное входное воздействие настроенного на МО токового контура в соответствии с таблицей 1 имеет вид:
i*a (τ) = i*уст (1−e−τ(cos(τ) +sin(τ))) , |
(5.61) |
где i*уст - относительное установившееся значение якорного тока;
τ = t / 2Tµ - относительное время.
Выражение (5.61) можно записать в следующем виде:
i*a (t) = i*уст (1−e− |
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
||||||
2Tµ |
(cos |
|
|
+sin |
|
|
) . |
(5.62) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Tµ |
|
|
2Tµ |
|
||||||
Продифференцировав выражение (5.62) получим изменение |
||||||||||||||||||||||||||||
производной якорного тока во времени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
di* |
|
i*уст |
|
|
|
− |
t |
|
|
|
|
t |
|
|
|
|
|
|
|||||||||
|
= |
e |
2Tµ sin |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(5.63) |
||||||||
|
|
Tµ |
|
|
|
2Tµ |
|
|
|
|
||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для определения максимума производной якорного тока |
||||||||||||||||||||||||||||
необходимо найти вторую производную тока: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
i*уст |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||||
d2i* |
|
2 |
|
|
|
|
|
− |
|
|
|
|
t |
|
π |
|
|
|
||||||||||
= |
|
|
|
e |
2Tµ sin( |
|
|
− |
) . |
|
||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.64) |
||||||||||||
|
2Tµ |
|
|
2Tµ |
4 |
|||||||||||||||||||||||
dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
226 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для определения экстремума первой производной необходимо приравнять нулю вторую производную:
|
|
|
i*уст |
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
d2i* |
|
|
2 |
|
|
− |
|
t |
|
|
π |
|
|
|
|||
|
= |
|
e |
2Tµ sin( |
|
0 |
− |
) = |
0. |
|
|||||||
a |
|
|
|
|
|
|
|
|
(5.65) |
||||||||
|
2Tµ |
|
|
2Tµ |
4 |
||||||||||||
dt2 |
t =t 0 |
|
|
|
|
|
|
|
|
|
|||||||
Из последнего |
выражения |
|
определим |
|
время t0 , при |
котором |
|||||||||||
di*a dt достигает максимума:
|
|
|
|
t |
0 |
= πT . |
|
|
(5.66) |
|||
|
|
|
|
|
2 |
µ |
|
|
|
|
||
Если t0 подставить в выражение |
(5.63), то получим |
значение |
||||||||||
максимума производной якорного тока: |
|
|
|
|
|
|||||||
di* |
|
|
|
|
i*уст |
−π |
|
|
π |
|
||
|
a |
|
|
|
|
|
|
4 |
|
|
|
|
|
= |
T e |
sin 4 . |
(5.67) |
||||||||
|
dt |
|
|
|
||||||||
|
|
max |
|
|
µ |
|
|
|
|
|
|
|
На практике вместо выражения (5.67) |
пользуются следующим |
|||||||||||
приближенным выражением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
di* |
|
|
|
|
|
|
i*уст |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
≈ 0,322 T . |
(5.68) |
|||||||||
|
dt |
|
|
|||||||||
|
|
|
max |
|
|
|
|
µ |
|
|
|
|
Пример 15. Определить максимальное значение производной якорного тока настроенного на МО токового контура (пример 5) при максимальном задании якорного тока (i*уст=2,5).
Для определения максимального значения производной якорного тока воспользуемся выражением (5.68): (di*a/dt)max = 0,322i*уст/Tμ = 0,322*2,5/0,01 = 80,5. Это превышает допустимую величину темпа
227
изменения якорного тока, равную 15 … 50, что делает невозможным пуск электродвигателя под отсечку.
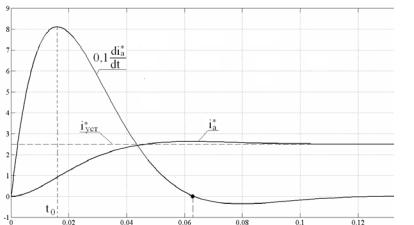
На рис.5.63 показаны переходные процессы для примера 15 реакции токового контура, настроенного на МО, на максимальное
скачкообразное задание i*уст = 2,5 и соответствующая производная якорного тока с коэффициентом передачи 0,1.
Как видно из рис.5.63 производная якорного тока достигает
максимума в момент времени t |
0 |
= |
πT = 3,14 * 0,01/ 2 = 0,0157 с, и |
|
|
2 µ |
максимальное значение производной якорного тока превышает 80 номинальных значений якорного тока в секунду.
Рис.5.63. Производная якорного тока при пуске под отсечку
Как видно из (5.68) снижение величины производной якорного тока возможно уменьшением величины i*уст , однако это повлечет за
собой снижение пускового момента, что нерационально с позиций использования перегрузочной способности электродвигателя. Снижение темпа нарастания тока якоря возможно за счет увеличения
некомпенсируемой постоянной времени Tµ . Однако, это тоже нежелательно, т.к. влечет уменьшение быстродействия токового контура.
Рассмотрим примеры снижения величины производной якорного тока, применяемые на практике.
228