metodLinAlg

Матриці та визначники.

1. Матриці та дії над ними

Матрицею називається система m × n чисел, розташованих в прямокутній таблиці з m рядків та n стовпців. Числа цієї таблиці називаються елементами матриці. Позначення матриці:

Елементи ai1, ai2,…,ain складають i -ий рядок (i=1,2,…,m) матриці,

елементи a1k, a2k,…,amk – її k -ий стовпець(k=1,2,…,n); aik- елемент, належить i -ому рядку та k -ому стовпцю матриці; числа i, k

називаються індексами елемента.

Матриця , яка містить m рядків та n стовпців, називається

матриця розміром m × n .

Дві матриці Am×n=(aik)m×n , Bp×q=(bik)p×q називаються рівними, якщо p=m, q=n та aik=bik (i=1,2,…,m; k=1,2,…,n); іншими словами якщо вони мають однакові розміри та їх відповідні елементи рівні між собою.

Матриця, яка складається лише з одного рядка, називається матриця-рядок. Матриця, яка складається лише з одного стовпця,

називається матриця-стовпець.

Матриця, всі елементи якої дорівнюють нулю, називається

нульовою.

3

Квадратною називається матриця, в якої число рядків дорівнює числу стовпців, тобто матриця вигляду

Порядком квадратної матриці називається число рядків (або стовпців).

Будемо казати, що елементи a11, a22,…,ann квадратної матриці утворюють її головну діагональ, а елементи a1n, a2n-1,…,an1 – другу діагональ.

Діагональною називається матриця, у якої всі елементи, які не належать головної діагоналі дорівнюють нулю.

Одинична матриця – це діагональна матриця, в якій всі елементи головної діагоналі дорівнюють одиниці.

Транспонована матриця до матриці А утворюється заміною місцями рядків зі стовпцями, виглядає як

Квадратна матриця, яка співпадає зі своєю транспонованою матрицею називається симетричною.

Для кожної матриці існує протилежна матриця :

А=[aij] -A=[- aij],

Таким чином А+(-А)=0.

Лінійними діями над матрицями називаються додавання та відіймання матриць, множення матриці на число. Додавання та відіймання матриць визначається тільки для матриць однакових розмірів.

4

Сумою матриць A=(aik)mn , B=(bik)mn називається така матриця

C=(cik)mn що

cik=aik+bik (i=1,2,…,m; k=1,2,…,n),

тобто матриця, елементи якої дорівнюють сумам відповідних елементів матриць-доданків. Сума двох матриць A i B позначається

A+B.

Різницею A-B матриць A=(aik)mn , B=(bik)mn називається матриця D=(dik)mn , для якої

dik=aik-bik (i=1,2,…,m; k=1,2,…,n).

Добутком матриці A=(aik)mn на число α ( або числа α на матрицю A) називається матриця B=(bik)mn, для якої

bik= α aik (i=1,2,…,m; k=1,2,…,n),

тобто матриця, яка отримана з даної множенням всіх елементів на число α. Добуток матриці на число позначається Aα або αA .

Добуток матриць визначається для матриць, в яких число стовбців першої матриці дорівнює числу рядків другої матриці. Такі матриці називаються зціпленими.

тобто елемент cik матриці Сml дорівнює сумі добутків елементів i -ого рядка матриці Amn на відповідні елементи k -ого стовпця матриці Bnl . Матриця Сml має m рядків та l стовпців. Добуток матриці A на матрицю B позначається AB .

З а у в а ж е н н я 1 . З того, що матицю A можна помножити на матрицю B не випливає, що матрицю B можна помножити на матрицю A. В загальному випадку AB≠BA. Якщо АВ=ВА, то матриці А та В називають перестановочні.

З а у в а ж е н н я 2 . АЕ=ЕА=А

5

Властивості матриць:

1. Додавання матриць є асоціативною та комутативною операцією.

2. Визначники та їх властивості Визначником квадратної матриці другого порядку

Aa11 a21 a21 a22

називається число, яке дорівнює а11а22 –а12а21 та позначається

детермінантом. Для визначника матриці А застосовують наступні позначення A , , det A, det(aik ).

Визначником квадратної матриці третього порядку

a11 a12 a13 a21 a22 a23 a31 a32 a33

6

називають алгебраїчну суму усіх можливих n! добутків елементів взятих по одному з кожного рядка та кожного стовпця:

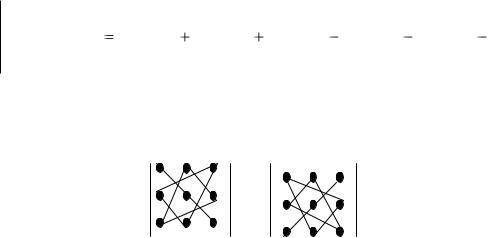
Це правило називається правилом Саріуса. Схематично можливо зобразити на рис.1.

+ ─

Рис.1.

Виродженою називається матриця, визначник якої дорівнює нулю. У протилежному випадку матриця є невироджена.

Мінором якого-небудь елементу визначника називається визначник, який утворюється з початкового шляхом викреслення рядка та стовпця, яким належить даний елемент. Мінор позначається М.

Алгебраїчне доповнення елемента аik визначника називається мінор зі своїм знаком, який визначається як (-1)i+k :

Аik=(-1)i+k Mik

Властивості визначників:

1)визначник не змінюється при зміні всіх рядків відповідними стовпцями;

2)при перестановці двох рядків (стовпців) визначник змінює знак;

3)визначник з двома однаковими рядками (стовпцями) дорівнює нулю;

4)множник, загальний для всіх елементів рядка (стовпця), можна винести за знак визначника);

7

5)визначник дорівнює нулю, якщо всі елементи рядка або стовпця дорівнюють нулю);

6)визначник не зміниться, якщо до елементів деякого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця);

7)визначник дорівнює сумі додатків елементів будь-якого рядка (стовпця) на їх алгебраїчне доповнення.

Властивість 7 можливо виразити формулою:

Надана формула представляє собою розклад визначника третього порядку за елементами першого рядка.

3. Обернена матриця.

Квадратна матриця А-1 називається оберненою до квадратною матриці А, якщо виконується умова

А-1 А= А А-1=Е,

де Е – одинична матриця.

Квадратна матриця називається невиродженою або неособливою, якщо її визначник відрізняється від нуля. Якщо визначник матриці дорівнює нулю, вона називається виродженою

або особливою.

Кожна невироджена матриця

має обернену матрицю

8

де Аik- алгебраїчне доповнення елемента аik матриці А.

~

Матриця A називається союзною або приєднаною:

4. Ранг матриці

Рангом матриці називається найвищий з порядків її мінорів, який не дорівнює нулю.

Тобто якщо в матриці хоча б один мінор другого порядку дорівнює нулю, а всі мінори третього порядку дорівнюють нулю, то ранг такої матриці дорівнює двом.

Ранг позначається r(A).

Для підрахування рангу матриці використовують елементарні перетворення:

1.Транспонування.

2.Заміна місцями рядків або стовпців.

3.Множення рядка (стовпця) на число.

4.Додавання до рядка (стовпця) елементів паралельного стовпця помноженого на одне і теж число.

Всі ці операції ми можемо використовувати тому, що нас цікавить лише дорівнює мінор нулю чи ні.

9

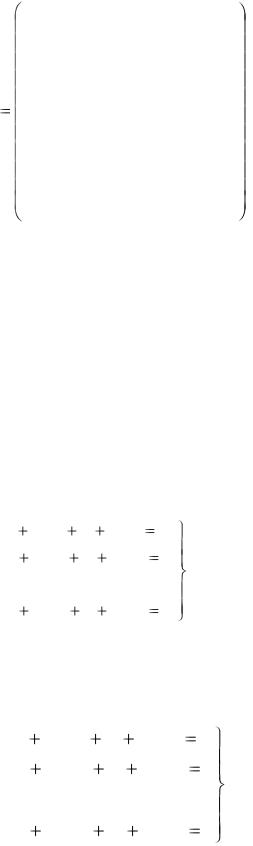
Елементарними перетвореннями будь-яку матрицю можна

Ранг буде дорівнювати кількості рядків, що містять одиниці.

Системи лінійних алгебраїчних рівнянь

Лінійним алгебраїчним рівнянням (ЛАР) називають рівняння, яке містить змінну лише у першій степені та не має добутку змінних. При розв’язку систем лінійних рівнянь використовують визначники та матриці.

Розглянемо систему n лінійних алгебраїчних рівнянь з n невідомими х1, х2, х3, хn:

Якщо хоча б один з вільних членів bi≠0 , то система рівнянь (1) називається неоднорідною. Якщо всі вільні члени bi = 0 (і=1,2,…, n ), то така система рівнянь називається однорідна та має вигляд

10