7. Исчисления высказываний

Чтобы задать и. в. нужно задать :

1. множество символов исчисления Х;

2. множество выражений Х^* (конечная последовательность символов)

3. множество формул исчисления ;

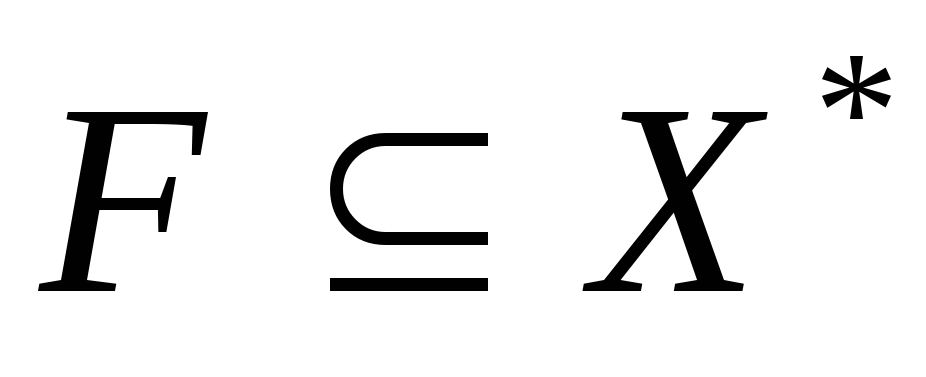
4. аксиома исчисления ;

5. правила вывода исчисления, которые есть формальные процедуры, которые по произвольным формулам и формулеА определяют выводима ли непосредственна формула А из формул . В случае, если формулаА выводима из непосредственно, этот факт записывают

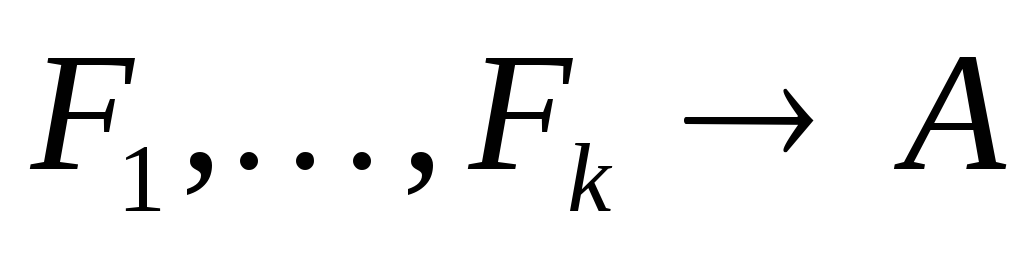
Формула А выводима в логическом исчислении, если существует последовательность формул , что последняя формула, и все формулы этой последовательности есть либо аксиомы логич. исчисления, либо непосредственно следуют из предыдущих формул или аксиом по правилам вывода данного исчисления. В этом случае говорят. Что формулаА является теоремой исчисления и записывают |-A.

Будем говорить, что А является следствием формул (гипотез) и записывать|-A если существует последовательность формул что последняя формула естьА и каждая формула в этой последовательности есть либо аксиома, либо непосредственное следствие формул (аксиом или гипотез) .

Свойства выводимости:

1) пусть из множества гипотез Г выводится формула А, множество ГΔ есть подмножество множества Δ, тогда формулаА есть следствие множества формул Δ |-A . Утверждение следует из того факта, что вывод формулы А из множества Г является выводом А из множества Δ, т. к. Δ .

2) пусть Г|-А , тогда конечное подмножествоГ’ множества Г такое, что Г’|-А . Это следует из того, что для формулы А по определению имеется конечный вывод из множества гипотез Г , поэтому кол-во используемых гипотез Г в этом выводе конечно, это множество и есть то конечное множество Г’ из которого следует формула А.

3) пусть Г|-А и каждая F из Г есть следствие формул Δ. Δ |-F , следовательно А есть следствие формул Δ : Δ |-A . Это следует из того, что в выводе формулы А из множества Г каждую гипотезу Г можно заменить их выводами из формул Δ , тогда получим вывод А из множества гипотез Δ.

1) символы исчисления высказываний есть счетная последовательность , бинарная связка ; унарная связка ; скобки (;).

2) выражения есть любые конечные последовательности символов исчисления

3) формулы — выражения вида , гдепеременные , есть формула.

Пусть выражение такого вида есть формула, тогда выражения,также является формулой.

4. аксиомы исчисления:

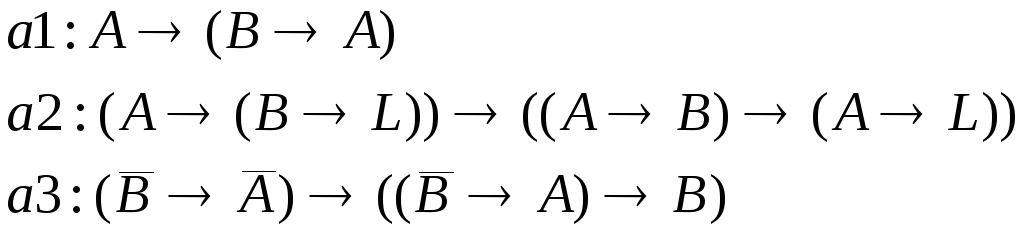
для любых формул A,B,L

6. правила вывода:

Modus ponens (MP):

Каждой построенной формуле нашего исчисления будет соответствовать логическая функция.

Тавтологией назовем функцию, которая на всех наборах принимает значение 1.

Каждая аксиома исчисления высказываний является тавтологией.

Допустим противное: существует набор, при котором

когда

противоречие . Покажем, что a2 тавтология, допустим противное

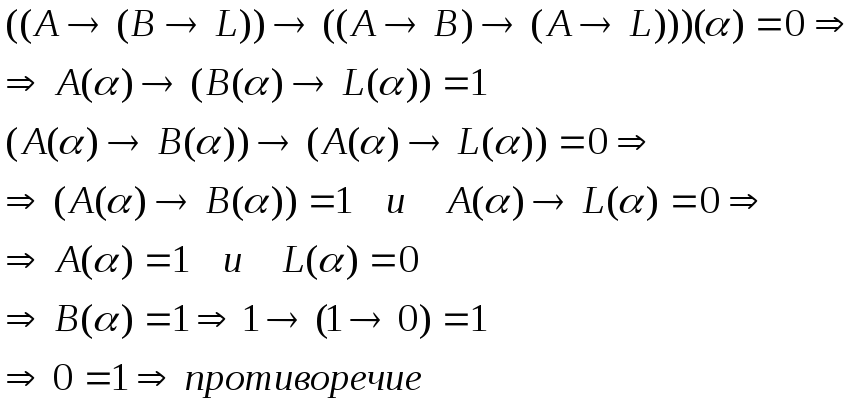
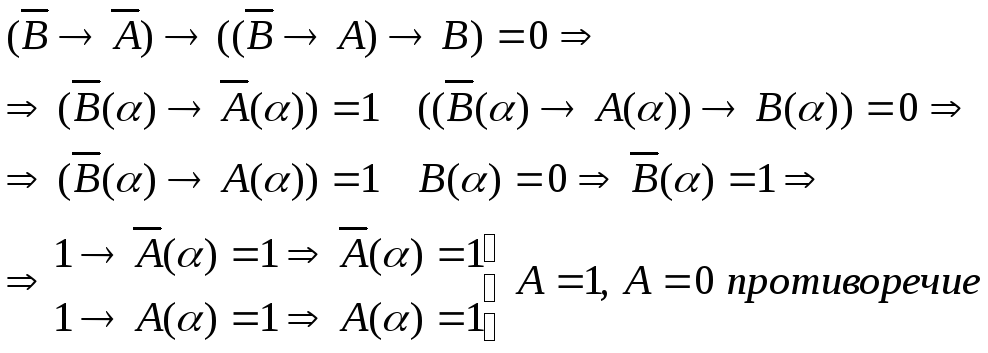
Правило МР сохраняет свойство формулы быть тавтологией, то есть непосредственное следствие двух тавтологий есть тавтология.

|-B

Доказательство:

Рассмотрим тавтологию А и , покажем что формулаВ следует из данных двух формул по правилу вывода МР есть тавтология. Допустим противное:

, т.к. А тавтология, не является тавтологией, получили противоречие, что и требовалось доказать.

Утверждение теоремы исчисления высказываний есть тавтология в силу того, что аксиомы есть тавтологии, а следствие из этих аксиом тогда также будут тавтологией в силу того, что МР сохраняет свойство тавтологии. Оказывается, что верно и обратное утверждение, то есть, если формула в связках () и () есть тавтология, то она выводима из множества аксиом исчисления.

Исчисления, обладающие данным свойством называются полными, т. е., если аксиомы заданные данным образом, что множество всех формул, выводимых из этих аксиом есть в точности все тавтологии, то тогда такое счисление называют полным.

1. В вычислении высказываний выводима . Запишем аксиому а2 в виде

, заменив L на А и В на , тогда видно, что левая часть данной формулы есть аксиома а1, где вместоВ подставлена

, тогда по МР из этих двух формул выводима правая часть данной формулы. Левая часть выведенной формулы есть аксиома а1, где вместо В стоит А, поэтому из предыдущей формулы по правилу МР выводима правая часть формулы.

Это и есть требуемая теорема.

Предложение 1:

Из формулы А для любой формулы В выводима ВА

Доказательство:

и а1, по правилу МР выводима правая часть.

Из формулы А выводима любая формула, где А стоит в правой части.

Теорема дедукции:

Из множества гипотез и формулы А выводима В , то из множествавыводима.

Доказательство:

Пусть вывод формулыВ из множества гипотез . Индукцией поГ докажем, что из множества гипотез выводима формула:

При j=1 В₁ есть либо одна из гипотез Г либо аксиома, либо формула А. В первых двух случаях данное утверждение следует из предложения. В оставшемся случае выводимая формула принимает вид . Но эта теорема в исчислении, следовательно доказательство при j=1 завершено.

Пусть утверждение верно для всех . Докажем утверждение для j:В_k есть либо одна из гипотез Г , либо аксиома, либо формула А, либо следует по правилу вывода из некоторых предыдущих формул В_j, B_s, где B_s имеет вид по правилу вывода . В первых трех случаях доказательство такое же, как и для j=1 . В оставшемся случае применим предположение индукции и аксиому а2: а именно: из предположения индукции следует, что из гипотезвыводятся формулыи, т.е..

Рассмотрим аксиому а2 в виде , тогда в силу того, что из множества гипотезвыводится левая часть этой аксиомы, то тогда в силу МР выводится и правая часть этой аксиомы. В силу того, что из множества гипотезвыводится левая часть полученной правой части, то выводится и правая часть:

Т.о. из множества гипотез выводится формула, ч.т.д.