Глава. Введение в теорию конечных автоматов.

Определение. Рассмотрим два конечных множества и . Будем называть их входным и выходным алфавитами соответственно. Элементы алфавитов будем называть буквами.

Все бесконечные последовательности букв алфавита будем обозначать и называть бесконечными словами. Символом будем обозначать всевозможные конечные слова в алфавите . Слова длины в алфавите будем обозначать – декартово произведение множества на себя раз. Скажем, что слово является началом слова или приставкой, если для некоторого слова . Длину конечного слова, т.е. число его букв, будем обозначать как.

Пример. – начало слова , где .

Пусть – конечное множество. Отношением на данном множестве будем называть его подмножество . Рассмотрим декартово произведение на себя: . Т.е. это множество всевозможных слов из двух букв в алфавите . Отношением эквивалентности называется подмножество декартового произведения, которое удовлетворяет следующих трем свойствам:

1. Рефлексивность. .

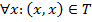2. Симметричность. .

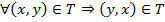3. Транзитивность. .

Примеры отношения эквивалентности.

Пример 1. Рассмотрим в качестве множества X множество натуральных чисел: . Для него рассмотрим обычное равенство натуральных чисел. Скажем, что два натуральных числа эквивалентны, если они равны в обычном смысле. Очевидно, что это есть отношение эквивалентности.

Пример 2. Рассмотрим произвольное натуральное число . Числа x и y назовем эквивалентными , если они дают один и тот же остаток при делении на . Очевидно, что это есть отношение эквивалентности.

Пример 3. Введем отношение эквивалентности на множестве слов, длина которых не меньше числа . Рассмотрим множество этих слов в алфавите . Скажем, что пара слов и эквивалентны, если совпадают их первые букв. Убедитесь сами, что все три свойства эквивалентности выполнены.

Утверждение. Пусть – множество, – отношение эквивалентности на нем. Тогда разбивает все элементы на классы эквивалентных элементов (Любая пара различных классов не пересекается между собой-, и их объединение совпадает с множеством;; количество классов может быть бесконечным). Любая пара элементов одного класса эквивалентна, а любая пара элементов различных классов не эквивалентна. Данное разбиение однозначно определяется отношением эквивалентности .

Докажите это утверждение самостоятельно.

Пример 1. Классы эквивалентности – одноэлементные подмножества , .

Пример 2. Пусть задано отношение эквивалентности на множестве натуральных чисел . Числа эквивалентны, если их остатки от деления на совпадают. Классы эквивалентности – , .

Пример 3. Если для тех же натуральных чисел взять вместо двух произвольное число , то число классов эквивалентности будет так же . По одному классу на каждый из их остатков.

Определение. Пусть заданы конечные алфавиты: – входной и – выходной. Задана функция , которая ставит в соответствие бесконечной последовательности из алфавита некоторую бесконечную последовательность алфавита . Функция называется детерминированной, если начало выходного слова однозначно определяется соответствующим началом входного слова, т.е. выполнено следующее формальное определение: (любая пара слов ,которые имеют одно и тоже начало преобразуются функцией в пару слов , которые имеют одно и тоже начало соответствующее началу ). Говоря другими словами, начало длины выходного слова не зависит от конца входного слова (начиная с -ой буквы).

Определение. Остаточной функцией, соответствующей слову и детерминированной функции , называют функцию , которая определяется следующим образом. Чтобы определить значение этой функции на входной последовательности , добавим к этому слову приставку , получим слово , применим к этому слову функцию , в результате получим слово и тогда значением объявим слово . ; ; ; ; ; .

Определение. Функция называется ограниченно-детерминированной, если число различных остаточных функций конечно.

Пример. Рассмотрим константно-периодическую функцию. Такая функция на любом входном слове равна одному и тому же выходному слову, и есть некоторое периодичное слово, бесконечное повторение некоторого конечного слова . Очевидно, что такая функция детерминированная, а число различных остаточных функций равно длине периода, т.е. длине слова .

Замечание. Каждая остаточная функция является детерминированной.

Дадим эквивалентное определение ограниченно-детерминированных функций в классе некоторых устройств, которые их вычисляют.

Определение. Конечным автоматом называют набор из шести множеств , где – входной алфавит, – выходной алфавит, – множество состояний автомата (конечные множества), , – функция переходов состояний ; – функция выходов автомата .

Автомат имеет две ленты (входную и выходную) и считывающий элемент, который в каждый момент времени находится в одном из своих состояний . Функционирование автомата однозначно определяется функцией переходов, функцией выходов и входным словом, которое написано на входной ленте. В начальный момент времени состояние автомата и он обозревает самую левую букву входного слова. Далее процесс вычисления происходит следующим образом: 1. Если в текущий момент времени считывающий элемент находится в состоянии , обозревая символ на входной ленте, то он переходит в состояние согласно функции переходов на паре ; на выходной ленте считывающий элемент печатает символ согласно функции выхода и сдвигается на ячейку вправо. После считывания входного слова, т.е. в момент времени равного длине входного слова, на выходной ленте будет написано некоторое выходное слово в алфавите . Это слово и объявляем выходом автомата на входном слове, записанном на ленте. Таким образом, автомат вычисляет некоторую словарную функцию , которую называют функцией соответствующего автомата, .

Утверждение. Каждая функция, которую реализует автомат, является ограниченно-детерминированной, и для любой ограниченно-детерминированной функции существует автомат её вычисляющий.

Для доказательства удобно рассматривать графовое представление автомата. Каждому состоянию автомата поставим в соответствие некоторую вершину графа. Переходы обозначим ориентированными ребрами и определим их по функции переходов и выходов автомата следующим образом. Пусть на паре значений функции переходов равно , а значение функции выходов , тогда из вершины в вершину направляем ориентированное ребро и помечаем ребро парой , где – входной символ и – выходной.

По любому входному словуможно определить выходное слово . следующим образом. Входное слово однозначно определяет некоторый путь в графе автомата, который помечен этим словом ( в силу однозначности и всюду определенности функций переходов и выходов автомата). Тогда, взяв соответствующие выходные буквы на ребрах данного пути мы получим требуемое выходное слово автомата на входе .

Очевидно, что выход автомата длины определен входом длины и не зависит от последних букв, которые будут подаваться автоматом в моменты времени. Таким образом, любой автомат вычисляет детерминированную функцию. Если пара слов и ведет в одно и то же состояние автомата , то его остаточные функции и будут равными. Какое бы слово не дописали к словам и , остаточный выход слова данного автомата будет один и тот же, т.к. на началах и автомат попадает в одно и то же состояние , а выходное слово однозначно определяется текущим состоянием и остаточным словом в текущий момент. Поэтому число остаточных функций не более числа состояний автомата, а это число конечно.

Таким образом, показано, что функция, которую вычисляет любой конечный автомат является ограниченно- детерминированной.

Теперь покажем, что для любой ограниченно-детерминированоой функции можно сопоставить конечный автомат, который ее вычисляет (т.е любая ограниченно-детерминированная фукция является автоматной).

Рассмотрим ограниченно-детерминированную функцию и построим по ней автомат, который ее вычисляет. Рассмотрим все различные остаточные функции которые соотвествуют конечным словам . Считаем, что – пустое слово, а соответствующая ему остаточная функция есть функция .

На множестве всех конечных слов введем отношение эквивалентности. Пару слов и объявим эквивалентными тогда и только тогда, когда соответствующие остаточные функции и равны. Нетрудно проверить, что данное определение действительно дает отношение эквивалентности на множестве конечных слов.

В итоге все множество конечным слов разбивается на классы эквивалентности, одним из представителей которых являются выбранные нами слова . Построим автомат.

Каждому слову поставим в соответствие состояние автомата, которое обозначим также символами .

Функцию переходов и функцию выходов автомата в состоянии построим по следующему правилу. К слову добавляем букву входного алфавита , в результате получим слово . Применяя ограниченно-детерминированную функцию, получаем , где – слово, а – буква выходного алфавита. Для слова находим эквивалентного представителясреди . Тогда из вершины направляем ориентированное ребро в вершину и помечаем это ребро парой букв . Данное построение совершаем для всех представителей и всех входных букв .

Начальным состоянием автомата объявляем (пустое слово).

В результате получаем всюду определенный и однозначный автомат.

Покажем корректность построения, т.е. что автомат действительно вычисляет ограниченно-детерминированную функцию .

Для этого достаточно доказать следующее утверждение.

Утверждение. Входное слово эквивалентно выбранному представителю тогда и только тогда, когда слова и в графе построенного автомата ведут в одно и то же состояние .

Доказательство.

Пусть слово ведет в состояние представителя . Покажем индукцией по длине слова ,что .Для пустого слова утверждение очевидно (слово длины 0 есть пустое слово- оно соответствует начальному состоянию). Пусть утверждение доказано для слов длины не более ,докажем его для слова длины Т.е.-слово имеет слово длины началом и оканчивается на букву .Пусть слово уведет в состояние представителя .Тогда по предположению индукции цией .

Замечание

Если к эквивалентным словам добавить любое, одно и тоже оканчание, то плученные слова также являются эквивалентными.

Если предположить противное: ,но при некотором получим не эквивалентные слова ,тогда остаточные функции словне равны, тогда слова не эквивалентны.

Таким образом, .Также по построению имеем .

По транзитивности отношения эквивалентности имеем .

Из доказанного непосредственно следует, что слова ведут в одно и тоже состояние

, тогда и только тогда, когда они эквивалентны. Если ведут в одно и тоже состояние , то по доказанному они эквивалентны , поэтому по транзитивности эквивалентны между собой. Пусть теперь ведет (по доказанному ), а ведет в другое состояние (по доказанному )т.е. . Предположив противное ,лполучим ). Противоречие. Утверждение доказано.

Основное утверждение корректности справедливо в силу замечания, и того факта, что слова ведущие в одно и тоже состояние автомата соответствуют одной и тойже остаточной функции.

Схемы автоматов.

Подобно конечным двоичным функциям, можно рассмотреть возможность представления автомата в виде схемы функциональных элементов. Отличие в том, что автомат имеет конечную память. Чтобы реализовать возможность памяти используется элемент задержки, выход которой в момент времени t+1 равен входу в предыдущий момент времени t, t=0…

Автомат однозначно определяется следующими итеративными соотношениями: где – дискретное время , – начальное состояние автомата (соответствующее начальному моменту времени),

и – входные состояние и символ на ленте, – выходной символ автомата в момоент времени функционирования автомата.

Элементом задержкой называют автомат, который осуществляет следующее преобразование:

Т.о. выход автомата в момент времени является входом этого автомата в предыдущий момент времени . Это преобразование действительно автоматное, оно записывается следующими итеративными соотношениями ():

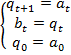
Постройте диаграмму автомата-задержки. Постройте диаграмму автомата-сумматора, который вычисляет сумму двух двоичных чисел (биты входных чисел считывать слева направо).

Рассмотрим базис из функциональных символов .

Функциональная схема в базисе определяется аналогично схеме из функциональных символов , ,.

Определение

Схемой в базисе на множестве входов,с множеством выходовзывается ориентированный граф с возможными циклами, входам которого (вершины из которых нет входящих ребер) приписаны входные переменные,выходам которой (вершины, в которые нет выходящих ребер) приписаны выходные переменный ,ельостальным вершинам приписаны функциональные элементы базиса ,причем в каждом цикле есть хотябы один элемент задержки.

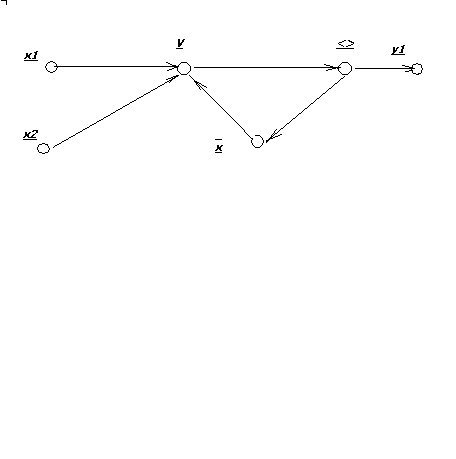
Замечание. В схеме, однако, допускаются циклы, но каждый цикл обязательно содержит хотя бы одну задержку.

Например, схема на рисунке имет входы– и выход –. Общая схема в рассмотренном базисе функционирует во времени..

Определение. Каждая схема в рассмотренном базисе реализует некоторую автоматную функцию следующим образом.

Рассмотрим произвольную схему в данном базисе. Пусть входам этой схемы приписаны переменные , а выходам переменные . Также элементы задержки приписаны вершинам . Входы этих вершин приписаны вершинам . Далее в графе схемы удалим ребра, сосединяющие вершины с (). Т.к. каждый цикл первоначального графа содержит хотя бы один элемент задержки, то получим после преобразования ациклический граф.

Объявим новыми входами схемы и припишем им входные переменные , а вершины объявим новыми выходами схемы, и припишем им переменные . Новые входы и выходы находятся во взаимно однозначном соответствии. Выходной переменной будет соответствовать входная переменная . Т.к. получена схема из функциональных элементов , то она определяет некоторый двоичный оператор . Выход есть двоичная функция от входных переменных .

Точно так же . есть некоторая функция от входных переменных. Естественно считать, что преобразование одномоментное, т.е. все преобразования производятся в один и тотже момент времени.

Теперь возвратимся к начальной схеме вычислений, т.е. восстановим элементы задержки выходного элемента задержки в момент времени . . Заменяя соответствующие переменные на , получаем автоматное преобразование:

Это и есть функциональное определение автомата.

Утверждение. Для каждой ограниченно-детерминированной функции существует схема в базисе , которая реализует данную автоматную функцию.

Доказательство.

Рассмотрим некоторое функциональное соотношение и построим схему, которая ее осуществляет. Не теряя общности будем считать, что входной и выходные алфавиты (в противном случае можно провести переобозначение – перейти к алфавиту

Рассмотрим соответствующие операторы и автомата. Это обычные двоичные операторы, каждый компонент которого – некоторая двоичная функция:

, векторная функция размерности .

, векторная функция состояний перехода.

, векторная функция выходов.

Т.к. это обычные двоичные операторы, то мы их можем реализовывать обычной функциональной схемой . Изобразим это представление на рисунке.

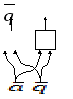
Схема слева на рисунке соответствует одномоментному преобразованию, реализует операторы и . Первоначальная схема реализует следующие двоичные операторы: и . Введем задержку между входом и выходом . При этом входные/выходные элементы связываются соотношением . Подставляя эти соотношения в предыдущие функции равенства, получаем искомую автоматную функцию.