3 Случай :

X	f0	f1
0	1	1
1	0	0

т.е .

Построим вывод :

Пусть и пара противоположных наборов, на которых значение функции одно и то же, и равно, для определенности нулю:.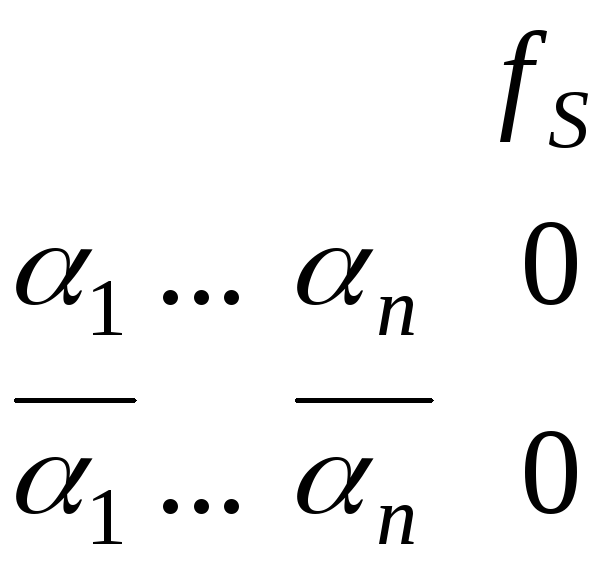

Разобьем множество всех переменных на две группы. В первую отнесем все переменные, которые равны нулю в первом наборе, во вторую, которые равны единице в первом наборе:

Теперь в переменные подставимx, а в подставим:.

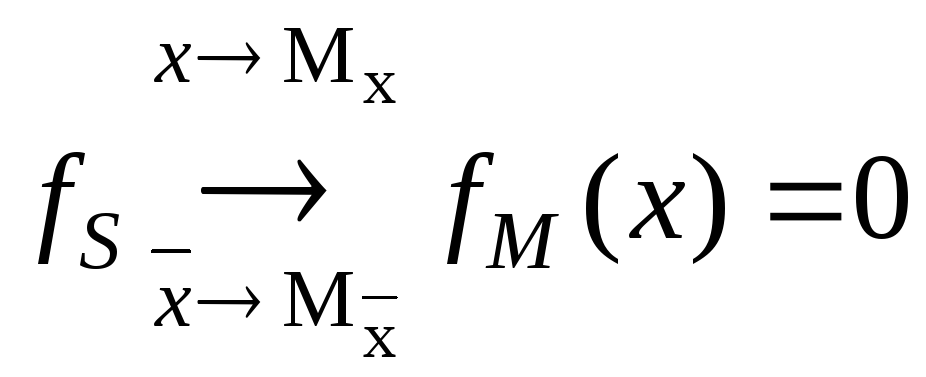Нетрудно видеть, что полученная функция есть константа 0, т.к. данная функция в нуле равна значению первоначальной функции на первом наборе, т.е. нулю, а в единице равна значению первоначальной функции на втором наборе, т.е. нулю. Константу 1 получим подстановкой 0 в функцию .

Например, пусть пара противоположных наборов, на которых равна нулю, имеют вид :

x1	x2	X3	x4	x5	f
0	1	1	0	1	0
1	0	0	1	0	0

Тогда .

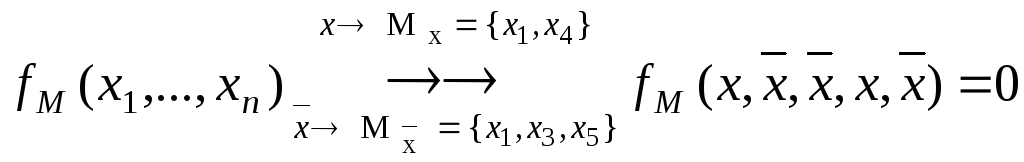Iый этап завершен.

II этап :

Построим вывод :

Рассмотрим полином Жегалкина функции..

В силу того, что  нелинейная, полином содержит по крайней мере одно слагаемое, которое есть конъюнкция по крайней мере двух переменных. Для определенности будем считать, что эта конъюнкция первых двух переменных. Используя дистрибутивность умножения относительно суммы, сгруппируем слагаемые следующим образом .

Из всех слагаемых, содержащих ивынесем за скобку конъюнкцию этих двух переменных; полином в скобках обозначим; из всех слагаемых, содержащих только,

вынесем за скобку :; из всех слагаемых, содержащих, вынесем:; останутся слагаемые, которые не содержат ни, ни, обозначим этот полином.

Из единственности полинома Жегалкина следует, что существует значениепеременных, при котором. Совершим соответствующие подстановки констант в нелинейную функцию.

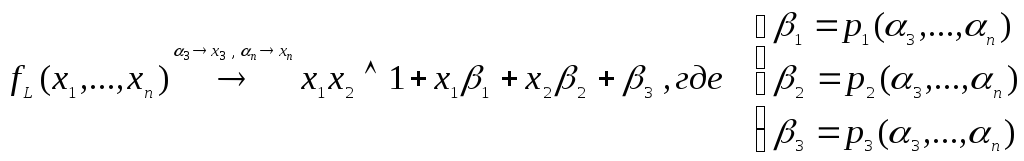Таким образом, получили функцию,

где некоторые константы.

Имеем восемь случаев :

1	2	3	f(x1,x2)
0	0	0
0	0	1
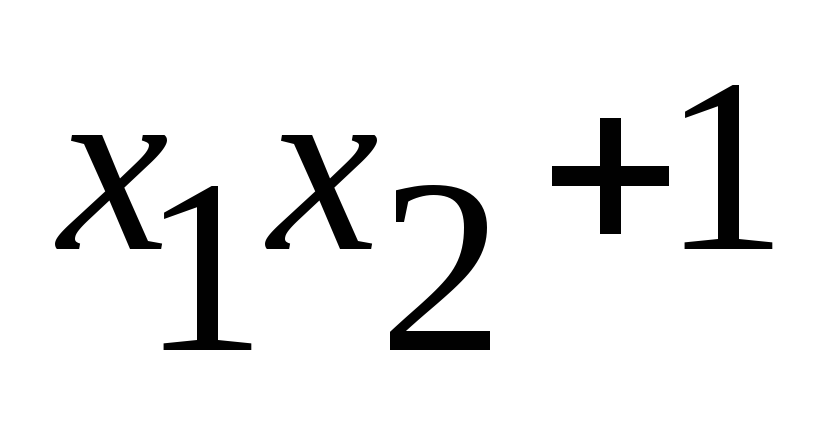
0	1	0
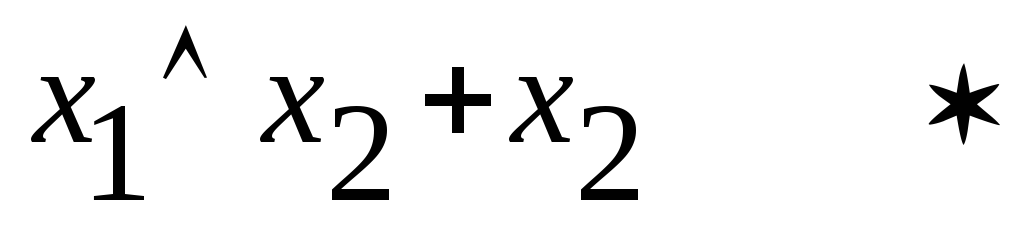
0	1	1
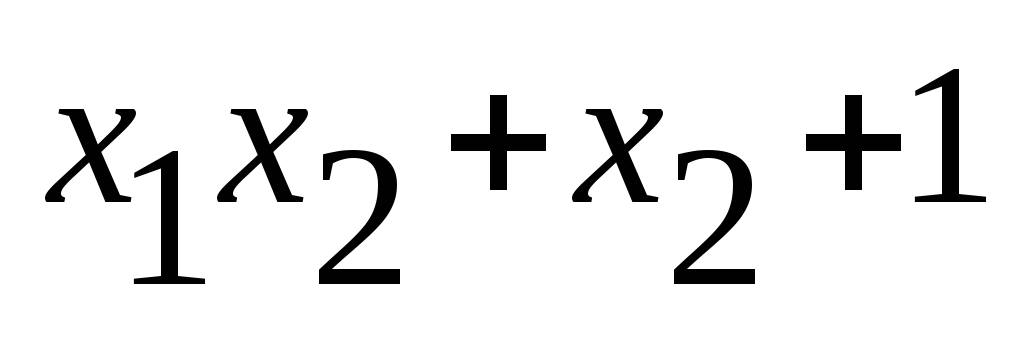
1	0	0
1	0	1
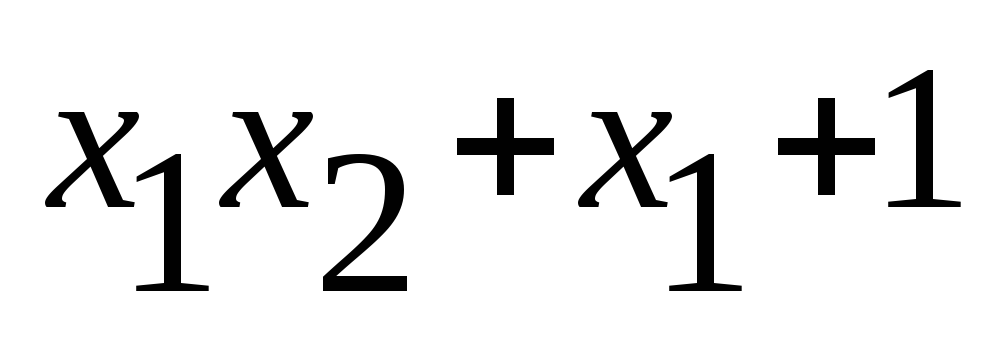
1	1	0
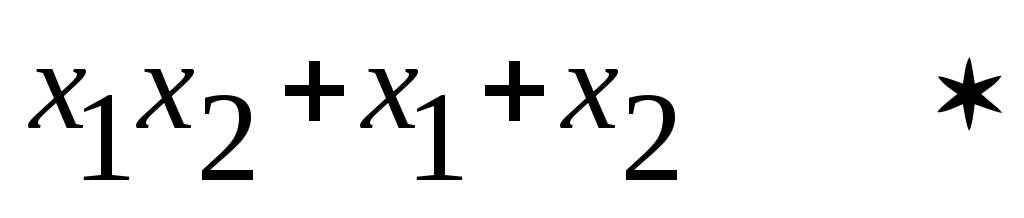
1	1	1

На самом деле достаточно рассмотреть всего лишь четыре случая, а именно, случай сводится к случаю, когдаподстановкой соответствующей функции в функцию отрицания.

Таким образом, достаточно рассмотреть случаи:

1); 2); 3); 4).

1. .

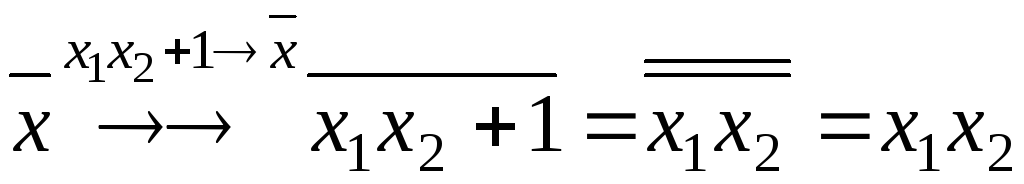Требуемая конъюнкция получена.

2) .

3) .

4)

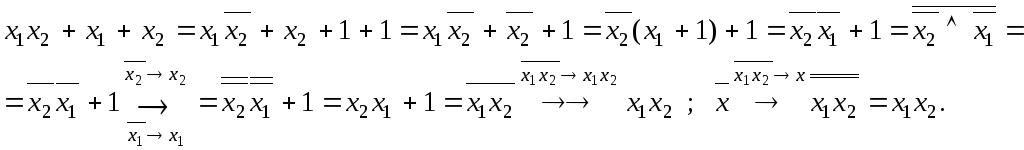
Например, из получим. После группировки слагаемых получаем, полиномравен 1, например, если,. Подставляем 1 в, 0 в, получаем функцию. Подставляемв переменную, получаем.

Упражнение 1: Исследовать на полноту:

1)

2)

3)

4)

5)

6)

Упражнение 2: Получить из функциифункции.

1)

2)

3)

4)

5)

0 0 0 1 1

0 0 1 0 0

0 1 0 1 0

0 1 1 0 0

1 0 0 1 0

1 0 1 0 0

1 1 0 1 0

1 1 1 0 0

Примеры:

1) Исследовать на полноту систему :

	T0	T1	S	M	L
f1	-	+	-	-	-
f2		-
f3

2) Исследовать на полноту систему

:

	T0	T1	S	M	L
f1	+	-	-	+	+
f2	-			+	+
f3				+	-
f4				+	-
f5				+

Система неполная, т.к. имонотонны, то и суперпозиция этих функций монотонны,поэтому пятая функция тоже монотонна.

Система принадлежит монотонному классу, поэтому неполна.

3) Можно ли из системы функций

получить функцию 0 :

	T0	T1	S	M	L
f1	-	-	+	-	+
f2			+
f3			+		+

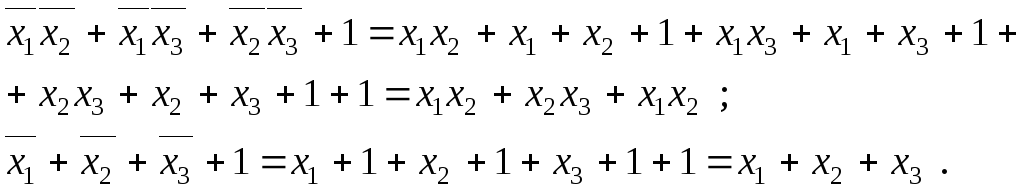
Система принадлежит классу самодвойственных функции, в силу замкнутости этого класса, и в силу несамодвойственности 0, получить 0 из функций системы нельзя.

4) Можно ли из системы функций

получить и, и если «да», опишите определяющие выражения :

	T0	T1	S	M	L
f1	+	-	-	-
f2	-
f3					-

Система полная, поэтому получить можно любые функции.

I :

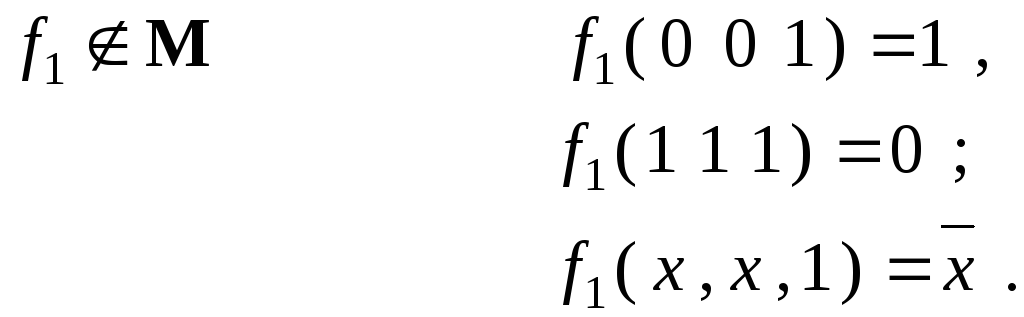
II:

5) Можно ли из системы функций

получить функции

, и если “да”, опишите определяющие выражения :

	T0	T1	S	M	L
f1	-	-	-	-
f2					-

x1	x2	x3	f1
0	0	0	1
0	0	1	0
0	1	0	0 -
0	1	1	1
1	0	0	0
1	0	1	0 -
1	1	0	1
1	1	1	0

I :

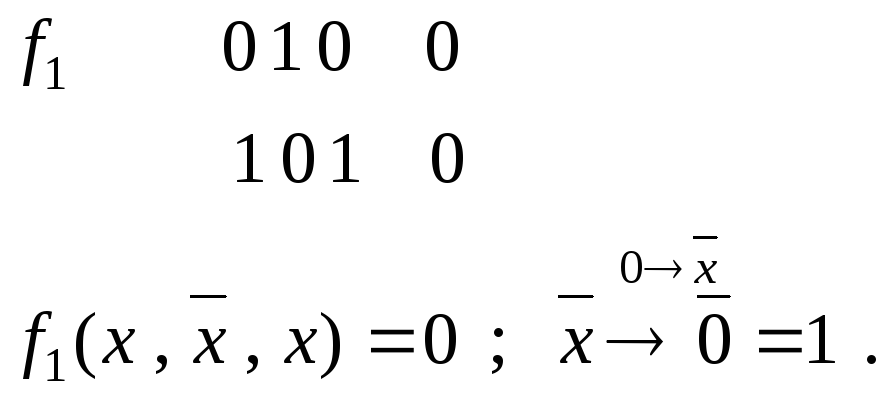
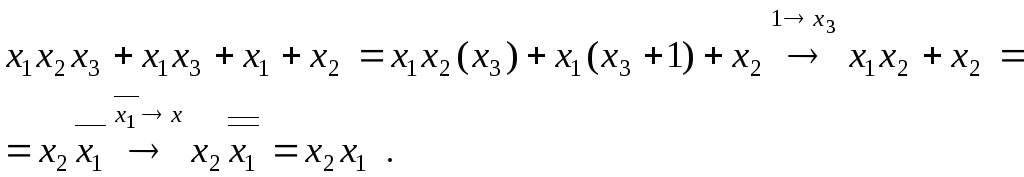
Упражнения : Исследовать на полноту системы :

1) ; 2); 3);

4) ; 5);

Можно ли из соответствующих систем функций получить следующие функции , и если “да”, то напишите определяющее выражение:

6) из системы функций получить функцию ;

7) из системы функций

получить функцию 0 ;

8) из системы функций получить функции ;

9) из системы функций

получить функции

;

10) из системы функций получить функции ;

Предполные классы булевых функций

Определение:

Предполным классом К называется неполный класс, при добавлении любой функции, которая не принадлежит ему, получается класс полный.

Утверждение:

Предполный класс является замкнутым.

Доказательство: Допустим противное, что некоторый предполный класс К не замкнут: , тогда рассмотрим функцию

т.е. [ K,f ] не полный

Теорема:

В классе булевох функций имеется ровно пять предполных классов :.

Доказательство :

В начале покажем, что данные классы являются предполными, а затем покажем, что других предполных классов нет.

1. Рассмотрим .

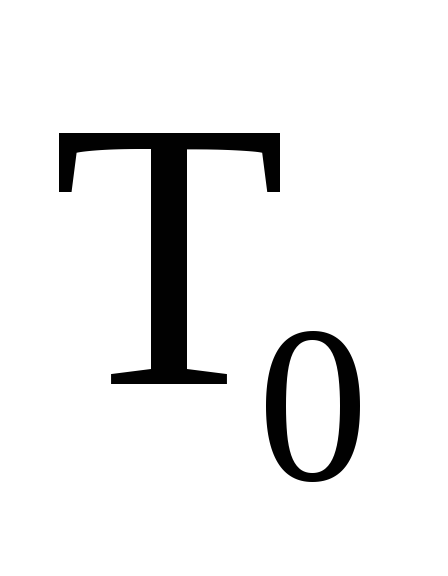Данный класс содержит функции:

поэтому класс Т₀ не принадлехит классам Т₁, S, М, L.

Рассмотрим произвольную , тогдане принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно классявляется предполным.

2) Рассмотрим Т₁:

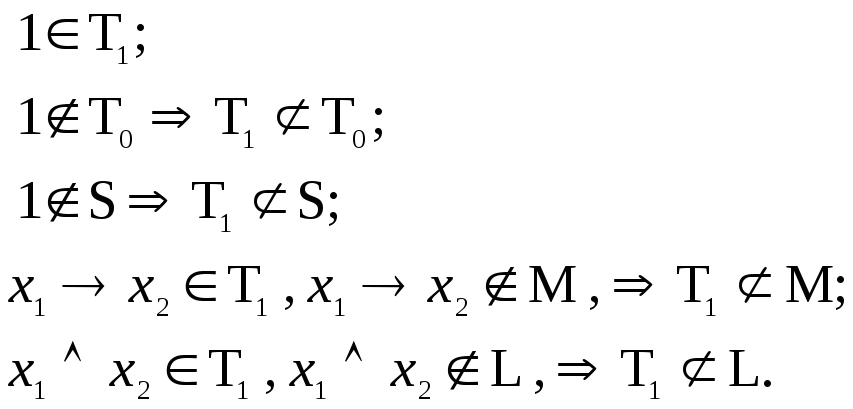
Рассмотрим произвольную не принадлежит ни одному из пяти классов, следовательно по теореме Поста является полной, следовательнопредполный.

3) Рассмотрим S:

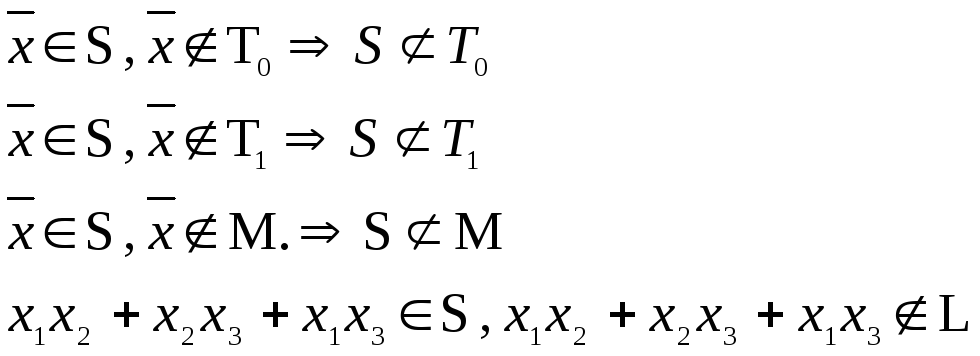
Рассмотрим не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательнопредполный .

4) Рассмотрим :

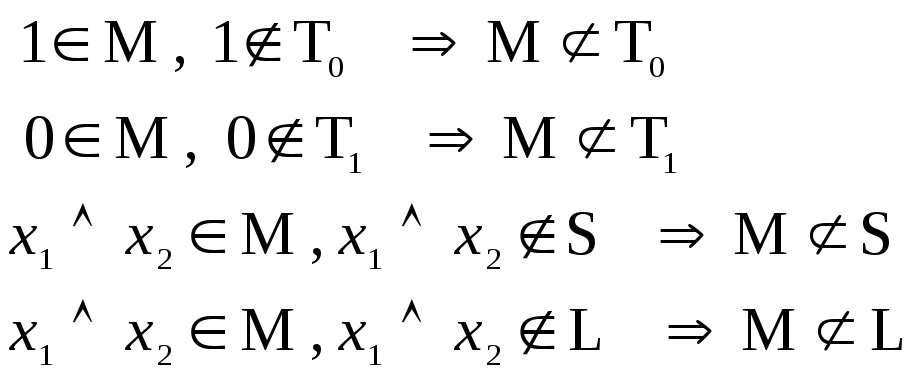
Рассмотрим не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательнопредполный.

5) Рассмотрим L:

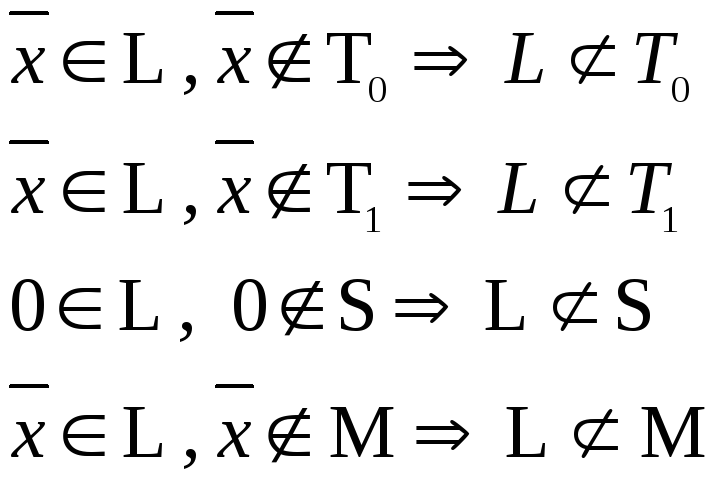
Рассмотрим не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательнопредполная. Все перечисленные классы не полны по теореме Поста.

Покажем, что других предполных классов в нет.

Допустим противное, что - предполный :

, следовательно в данном классе :

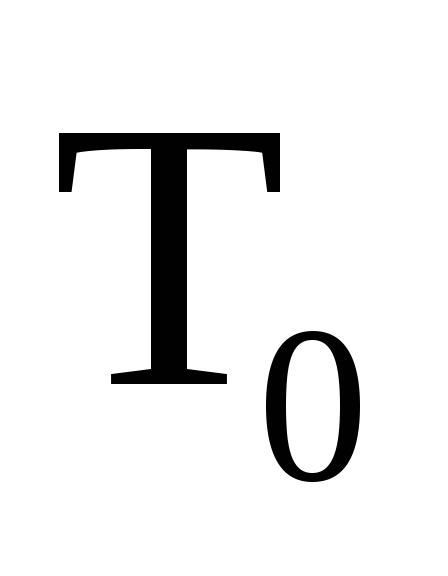
РИС.1

в силу того, что класс - предполный, следовательно включение на рис.1 невозможно, т.к. если бы было наоборот, то рассмотрим, мы бы получили, что все функции системысохраняют 0, поэтому полной системане является, следовательноне является предполным.

По этой же причине в классе должна быть,, должна быть, должна быть, должна быть, следовательно из этих включений следует, что системаявляется полной, противоречие с предполнотой этой системы.

Упражнения:

Найдите определяющие выражения функций через суперпозиции функций системы.

1)

2)

3)

4)

5)

Полные системы в классах булевых функций.

Определение:

Полной системой бул. функций в замкнутом классе К является система функций, которая принадлежит данному классу и замыкание которой совпадает с самим классом

Определение:

Базисом в замкнутом классе К называют систему В, которая полна в этом классе, но любая собственная подсистема полной не является.

Пример 1: Рассмотрим множество всех булевых функций Р₂. В этом множестве рассмотрим систему .Эта система полна по т. Поста .

Чтобы определить,что все собственные подсистемы не полны, достаточно рассмотреть лишь максимальные по включению собственные подсистемы данной, получаемые из данной удалением какой-либо функции.

Если ни одна из этих подсистем не является полной, то полной не является и любая другая собственная подсистема (докажите предыдущие утвеждения)

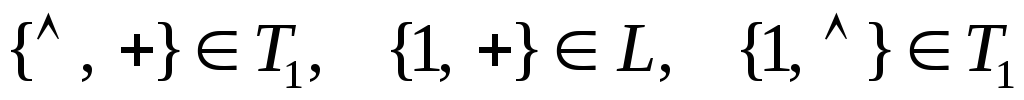
В данном примере максимальные собственные подсистемы не полны, значит является базисом вР₂.

Пример 2: Является ли система базисом вР₂?

, поэтому система полна, но собственная подсистематакже полна, поэтому данная система не базис вР₂.

Определение:

Скажем, что функция f не зависима от системы , если эта функция не принадлежит замыканию системы :.

Пример 1: Рассмотрим функцию и систему:

Утверждаем, что не зависит от этой системы. Действительно, все функции системы являются линейными, поэтому в силу того, что суперпозиция линейных функций есть линейная функция, замыкание этой системы принадлежит классу линейных функций, а— функция не линейная. Поэтомуне зависит от данной системы функций.

Пример 2: Рассмотрим функцию и систему:

x₁ x₂

0 0 1 0 0

0 1 1 1 1

1 0 0 1 1

1 1 1 1 1

Значит, зависима от функции.

Примечание: если функция не является независимой от системы, то будем называть ее зависимой от данной системы.

Утверждение:

Если система функций базис в замкнутом классе К , то тогда каждая функция базиса независима от оставшихся.

Доказательство:

Предположим противное: пусть существует базис в котором некоторая функция является зависимой от оставшихся. Для определенности будем считать, что этовыражается через некоторые суперпозиции функций системы, но тогда систематакже является полной в классеК, поэтому не является базисом. Утверждение доказано.

Пример 1:

базис в Р₂

Упражнение: Докажите справедливость обратного утверждения: пусть полная система в К, и любая функция системы не зависит от оставшихся, тогда система – базис в К.