
Методы оптимальных решений
.doc
-
Понятие экономико-математической модели. Примеры.
-
Понятие статической задачи оптимизации.
-
Критерий оптимизации, целевая функция, локальный экстремум, глобальный экстремум.
-
Понятие задачи линейного программирования.
-
Геометрический метод решения задач линейного программирования.
-
Геометрическая интерпретация симплексного метода.
-
Алгоритм симплексного метода.
-
Симплексные таблицы.
-
Метод искусственного базиса.
-
Составление математических моделей двойственных задач.
-
Первая теорема двойственности. Вторая теорема двойственности.
-
Двойственный симплексный метод.
-
Экономико-математическая модель транспортной задачи.
-
Нахождение опорного решения транспортной задачи: метод «северо-западного» угла.
-
Проверка опорного решения на оптимальность методом потенциалов.
-
Алгоритм решения транспортной задачи.
-
Транспортная задача с ограничениями на пропускную способность.
-
Транспортная задача по критерию времени.
-
Постановка задачи целочисленного программирования.
-
Примеры задач целочисленного программирования.
-
Метод ветвей и границ.
-
Понятие метода динамического программирования. Примеры задач.
-
Основные понятия теории игр. Равновесная ситуация: нижняя и верхняя цена игры, седловая точка.
-
Игра в смешанных стратегиях. Аналитическое решение игры
 .
. -
Правило доминирования стратегий.
-
Графическое решение игры вида
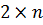 .
. -
Графическое решение игры вида
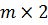 .
. -
Постановка задачи игры «с природой».
-
Критерии принятия решения в играх «с природой».
-
Понятие позиционной игры.
-
Нормализация позиционной игры.
-
Понятие графа. Способы задания графа. Петля, путь, цикл на графе. Простой путь, простой цикл на графе.
-
Способы задания графов .Задание графов с помощью матриц смежности и инциденций.
-
Упорядочивание дуг и вершин орграфа.
-
Алгоритм Дейкстры нахождения минимального пути.
-
Алгоритм Беллмана-Мура нахождения минимального пути.
-
Алгоритм нахождения максимального пути на графе.
-
Основные понятия элементов сетевого планирования. Работа, событие, критический срок, критические и некритические работы.
-
Использование линейных графиков в сетевом планировании. Вычисление резервов времени работ с помощью линейного графика.
-
Оптимизационные задачи сетевого планирования. Задача о сохранении срока выполнения комплекса работ при ограниченных ресурсах.
5.4.1. Основная литература
http://knigafund.ru/
-
Балдин К.В., Рукосуев А.В., Брызгалов Н.А. Математическое программирование: учебник/ Балдин К.В., Рукосуев А.В., Брызгалов Н.А.; Издательство « Дашков и К», 2012. – 218с. [Электронный ресурс]. – Режим доступа: http://www.knigafund.ru/books/16956 (дата обращения 09.05.2013)
-
Колобашкина Л.В. Основы теории игр: учебное пособие/ Колобашкина Л.В.; Издательство «БИНОМ. Лаборатория знаний», 2011. - 163с. [Электронный ресурс]. – Режим доступа: http://www.knigafund.ru/books/68179 (дата обращения 09.05.2013)
-
Федоров В.В., Сухарев А.Г., Тимохов А.В. Курс методов оптимизации: учебное пособие/ Федоров В.В., Сухарев А.Г., Тимохов А.В.; Издательство «ФИЗМАТЛИТ», 2011. - 368с. [Электронный ресурс]. – Режим доступа:http://www.knigafund.ru/books/112553 (дата обращения 09.05.2013)
5.4.2. Дополнительная литература
-
Ахтямов А. М. Математика для социологов и экономистов : учебное пособие для вузов / А. М. Ахтямов. - 2-е изд., испр. и доп. - М.: Физматлит, 2008. - 464 с.
-
Виленкин И. В. Высшая математика для студентов экономических, технических, естественно-научных специальностей вузов: учеб. пособие / И. В. Виленкин, В. М. Гробер. - 5-е изд. - Ростов н/Д : Феникс, 2009. - 415 с.
-
Высшая математика для экономистов: учеб. для студентов вузов, обучающихся по экон. специальностям / Н. Ш. Кремер [и др.]; под ред. Н. Ш. Кремера. - 3-е изд. - М. : ЮНИТИ, 2008. - 479 с.
-
Чупрынов Б.П. Математика в экономике: математические методы и модели: учебник для бакалавров/ Б.П.Чупрынов. – 2-е изд. – М.: Юрайт, 2013. – 541с.
5.4.3. Программное обеспечение и Интернет-ресурсы
-
Киселева Э.В., Соловьева С.И. Математическое программирование (линейное программирование): Учебное пособие. - Новосибирск: НГАСУ, 2002. - 146 с. [Электронный ресурс]. – Режим доступа: http://window.edu.ru/resource/315/63315 (дата обращения 15.04.2013)
-
Лутманов С.В. Линейные задачи оптимизации: Учебное пособие. Ч.1. Линейное программирование. - Пермь: Перм. гос. ун-т, 2004. - 128 с. [Электронный ресурс]. – Режим доступа: http://window.edu.ru/resource/587/50587 (дата обращения 15.04.2013)
-
Лутманов С.В. Линейные задачи оптимизации: Учебное пособие. Ч.2. Оптимальное управление линейными динамическими объектами. - Пермь: Перм. гос. ун-т, 2005. - 195 с. [Электронный ресурс]. – Режим доступа: http://window.edu.ru/resource/588/50588 (дата обращения 15.04.2013)
-
Рейзлин В.И. Численные методы оптимизации: учебное пособие / В.И. Рейзлин; Томский политехнический университет. - Томск: Изд-во ТПУ, 2011. - 105 с. [Электронный ресурс]. – Режим доступа: http://window.edu.ru/resource/650/75650 (дата обращения 15.04.2013)
-
Ромашова О.Ю. Методы оптимизации и расчеты на ЭВМ технико-экономических задач: учебное пособие. - Томск: Изд-во ТПУ, 2009. - 210 с. [Электронный ресурс]. – Режим доступа: http://window.edu.ru/resource/676/75676 (дата обращения 15.04.2013)
5.5.
