
- •1. Классификация случайных событий: возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры.
- •2. Полная группа событий. Пространство элементарных исходов. Примеры.
- •3. Классическое определение вероятности события. Свойства вероятности события. Примеры.
- •4. Статистическое определение вероятности события. Примеры. Теорема Бернулли (с доказательством).
- •5. Геометрическое определение вероятности. Примеры.
- •6. Сумма событий и ее свойства. Примеры.
- •7. Теорема сложения вероятностей (с доказательством) и ее следствия. Примеры. 8 Произведение событий и его свойства.
- •9. Условная вероятность. Зависимые и независимые события. Теорема умножения вероятностей (с доказательством). Примеры
- •11. Случайная величина (определение). Дискретная случайная величина и ее закон (ряд) распределения. Основное свойство закона распределения. Примеры.
- •Определение независимости случайных величин.
- •13.* Математические операции над дискретными случайными величинами. Примеры.
- •14. Функция распределения случайной величины, ее определение, свойства и график. Примеры.
- •15. Функция распределения дискретной случайной величины. Примеры.
- •16. Теорема о существовании случайной величины с заданной функцией распределения. Непрерывная случайная величина. Вероятность отдельно взятого значения непрерывной случайной величины. Примеры.
- •18. Математическое ожидание случайной величины и его свойства. Примеры
- •Свойства математического ожидания
- •Доказательство:
- •19. Дисперсия случайной величины и ее свойства. Среднее квадратическое отклонение случайной величины. Примеры.
- •1. Дискретная случайная величина, закон и функция распределения
- •2. Числовые характеристики дискретных случайных величин
- •20. Закон распределения Бернулли, его определение, свойства и примеры.
- •21. Биномиальный закон распределения, его определение, свойства и примеры.
- •22.Закон распределения Пуассона, его определение, свойства и примеры.
- •25. Нормальный (гауссовский) закон распределения.
- •26. Стандартный нормальный закон распределения. Функция Гаусса, ее свойства и график. Теорема о связи плотности нормального закона распределения и функции Гаусса.
- •27. Функция Лапласа, ее свойства, график и геометрический смысл. Теорема о связи функции распределения нормального закона и функции Лапласа. Примеры.
- •28.* Свойства случайной величины, распределенной по нормальному закону. Правило трех сигм. Примеры.
- •29.* Показательный (экспоненциальный) закон распределения, его определение, свойства и примеры.
- •34. Лемма Чебышева. Примеры
- •35. Неравенство Чебышева. Примеры
- •36. Понятие двумерной (n-мерной) случайной величины. Примеры. Одномерные распределения ее составляющих. Условные распределения.
- •37. Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин
20. Закон распределения Бернулли, его определение, свойства и примеры.
Дискретная случайная величина X имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, …, n, с соответствующими вероятностями:
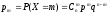 ,
где
,
где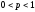 ,
,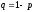 ,
,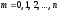 .
.
Математическое ожидание и дисперсия случайной величины X, имеющей биномиальное распределение, находятся по формулам:
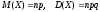 .
.
Из формулы Бернулли следует, что случайная
величина
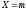 –
число наступлений события
–
число наступлений события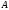 в
в независимых испытаниях (
независимых испытаниях ( )
– распределена по биномиальному закону.
)
– распределена по биномиальному закону.
21. Биномиальный закон распределения, его определение, свойства и примеры.
Пусть производится n независимых испытаний, в каждом из которых событиеAможет появиться или не появиться. Вероятность наступления события во всех испытаниях постоянна и равнаp(следовательно, вероятность непоявленияq = 1 - p).
Рассмотрим случайную величину X– число появлений событияAв этих испытаниях. Случайная величинаXпринимает значения0,1,2,…nс вероятностями,
вычисленными по формуле Бернулли: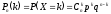 ,
гдеk = 0,1,2,…n.
,
гдеk = 0,1,2,…n.
Определение:Биномиальнымназывают раcпределение вероятностей, определяемое формулой Бернулли.
Пример. По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величинаX– число попаданий в мишень. Найти ее ряд распределения.
Решение: Случайная величинаXпринимает значения0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, гдеn = 3, p = 0,8(вероятность попадания),q = 1 - 0,8 = = 0,2(вероятность непопадания).
Тогда
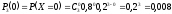 ,
,
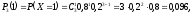
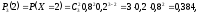
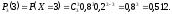
Таким образом, ряд распределения имеет следующий вид:
|
0 |
1 |
2 |
3 |
|
0,008 |
0,096 |
0,384 |
0,512 |
Пользоваться формулой Бернулли при больших значениях nдостаточно трудно, поэтому для подсчета соответствующих вероятностей используют локальную теорему Лапласа, которая позволяет приближенно найти вероятность появления события ровноkраз вnиспытаниях, если число испытаний достаточно велико.
22.Закон распределения Пуассона, его определение, свойства и примеры.
Определение. Будем говорить, что случайная величинаε распределена по закону Пуассона с параметромλ , если она принимает значения из множества { 0,1,…,n, …} с вероятностямиP{ε=m} = (λm/m!)*e-λ.
Теорема. Если случайная величинаε распределена по закону Пуассона с параметромλ , то и математическое ожидание, и дисперсия этой случайной величины равны параметруλ.
Свойства распределения Пуассона:
1.
![]() .
.
Действительно:
2.
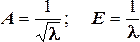 .
.
3.
если
![]() , то из биномиального распределения
следует закон распределения Пуассона.
, то из биномиального распределения
следует закон распределения Пуассона.
ПРИМЕР 1.Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут: а) три негодных изделия; б) не более трёх повреждённых изделия.
Решение:
по условию n=5000,
p=0,0002.
Найдём
![]() .
.
а) k = 3. Искомая вероятность по формуле Пуассона приближённо равна
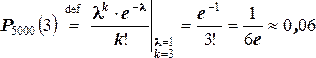 .
.
б)
Пусть случайная величина Х
– число изделий, повреждённых в пути,
то есть
![]() .
Очевидно, что данная случайная величина
распределена по биномиальному закону.
Следовательно, искомую вероятность
можно вычислить по формуле
.
Очевидно, что данная случайная величина
распределена по биномиальному закону.
Следовательно, искомую вероятность
можно вычислить по формуле
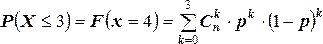 .
.
Но,
так как
![]() ,
то по свойству 3о
можем воспользоваться законом
распределения Пуассона, то есть, можем
записать:
,
то по свойству 3о
можем воспользоваться законом
распределения Пуассона, то есть, можем
записать:
 .
.
Замечание.По
формуле Пуассона можно вычислить
вероятность того, что число событий,
происшедших за время
![]() равно
равно![]() ,
если события образуют пуассоновский
поток, причём
,
если события образуют пуассоновский
поток, причём![]() –
интенсивность потока, то есть среднее
число событий, которые появляются в
единицу времени:
–
интенсивность потока, то есть среднее
число событий, которые появляются в
единицу времени:
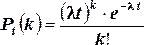 .
.
ПРИМЕР 2. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течении которых телефонистка отлучилась, не будет ни одного вызова?
Решение:
Найдём, прежде всего,
![]() –
среднее число вызовов за 1 секунду:
–
среднее число вызовов за 1 секунду:
![]() .
.
Тогда,
при
![]() ,
получим:
,
получим:
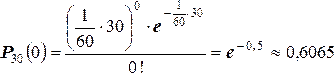
23.* Геометрическое распределение, его определение, свойства и примеры.
Пусть
проводятся независимые испытания,
каждое испытание может иметь два исхода:
удача с вероятностью p и неудача с
вероятностью q = 1 - p. Введем в рассмотрение
случайную величину X — число испытаний
до первого появления удачи. Эта случайная
величина может принимать значения 1, 2,
3, 4 и так далее до бесконечности. Когда
говорят, что случайная величина X имеет
значение k, то это означает, что первые
k - 1 испытание закончились неудачей, а
k-ое испытание стало удачным. Вероятность
того, что в серии независимых испытаний
будет вначале k - 1 неудач, а в k-ое
испытание — удача, равна
![]() .
Таким образом мы получили закон
распределения случайной величины X:
значению k случайной величины соответствует
вероятность
.
Таким образом мы получили закон
распределения случайной величины X:
значению k случайной величины соответствует
вероятность![]() .
Этот закон распределения и называется
геометрическим распределением
.
Этот закон распределения и называется
геометрическим распределением![]() .
Название происходит из того, что величина
.
Название происходит из того, что величина![]() представляет
собой геометрическую прогрессию, с
первым членом p и знаменателем q.Изучим
теперь свойства этого распределения.
С ростом k вероятности убывают. Используя
формулу для суммы членов геометрической
прогрессии, можем записать:
представляет
собой геометрическую прогрессию, с
первым членом p и знаменателем q.Изучим
теперь свойства этого распределения.
С ростом k вероятности убывают. Используя
формулу для суммы членов геометрической
прогрессии, можем записать: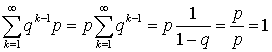 ,
то есть условие, что сумма всех вероятностей
в законе распределения равна единице,
выполнено. Вычислим теперь математическое
ожидание и дисперсию. По определению
математического ожидания имеем:
,
то есть условие, что сумма всех вероятностей
в законе распределения равна единице,
выполнено. Вычислим теперь математическое
ожидание и дисперсию. По определению
математического ожидания имеем: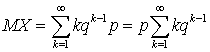 .
Для вычисления суммы воспользуемся
следующим приемом — заменим
.
Для вычисления суммы воспользуемся
следующим приемом — заменим![]() на
на![]() и
вынесем производную за знак суммы, в
итоге получим:
и
вынесем производную за знак суммы, в
итоге получим: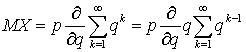 .
Оставшаяся сумма представляет собой
сумму членов геометрической прогрессии
и равна
.
Оставшаяся сумма представляет собой
сумму членов геометрической прогрессии
и равна![]() .
Вычисляя производную, запишем:
.
Вычисляя производную, запишем: .
Аналогично можно получить выражение
для
.
Аналогично можно получить выражение
для![]() :
: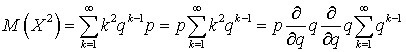 .
Заменяя сумму на ее значение
.
Заменяя сумму на ее значение![]() ,
вычисляем:
,
вычисляем: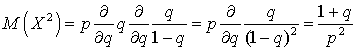 .
Таким образом, имеем выражение для
дисперсии:
.
Таким образом, имеем выражение для
дисперсии: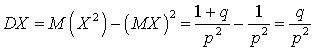 .
Если вероятность удачи равна единице,
то математическое ожидание числа
испытаний до первой удачи равно 1, а
дисперсия — 0. Если, наоборот,
вероятность удачи равна нулю, то
математическое ожидание — бесконечность
(то есть нужно произвести бесконечное
число испытаний до появления удачи).Пример
30.1Вероятность попадания в мишень из
винтовки равна 0,8. Найти математическое
ожидание и дисперсию случайной величины —
количества выстрелов до первого
попадания.Математическое ожидание
.
Если вероятность удачи равна единице,
то математическое ожидание числа
испытаний до первой удачи равно 1, а
дисперсия — 0. Если, наоборот,
вероятность удачи равна нулю, то
математическое ожидание — бесконечность
(то есть нужно произвести бесконечное
число испытаний до появления удачи).Пример
30.1Вероятность попадания в мишень из
винтовки равна 0,8. Найти математическое
ожидание и дисперсию случайной величины —
количества выстрелов до первого
попадания.Математическое ожидание![]() ,
дисперсия
,
дисперсия![]() .
Полученные результаты означают, что
при вероятности попадания 0,8 попадание
будет в среднем с 1—2 выстрела.
.
Полученные результаты означают, что
при вероятности попадания 0,8 попадание
будет в среднем с 1—2 выстрела.
24.Равномерный закон распределения, его определение, свойства и примеры. Законы распределения НСВ Плотности распределения НСВ называют также законами распределения. Часто встречаются законы равномерного, нормального и показательного распределений.
Определение.1.
Закон распределения НСВ
![]() называется
равномерным, если ее плотность
распределения задается в виде:
называется
равномерным, если ее плотность
распределения задается в виде:
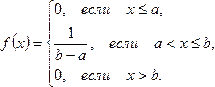 1.
Зная плотность распределения, и используя
формулу
1.
Зная плотность распределения, и используя
формулу
![]() ,
,
можно найти функцию распределения:
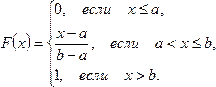
2.
Если НСВ
![]() имеет
равномерное распределение, то ее числовые
характеристики могут быть найдены по
формулам:
имеет
равномерное распределение, то ее числовые
характеристики могут быть найдены по
формулам:
![]() .
.
3.
Вероятность попадания равномерно-распределенной
НСВ
![]() в
интервал
в
интервал![]() можно
определить по формуле:
можно
определить по формуле:
![]() .
.
Пример
1.
Автобусы подходят к остановке с интервалом
в 5 минут. Считая, что НСВ
![]() -
время ожидания автобуса - распределена
равномерно, найти среднее время ожидания
(математическое ожидание), среднее
квадратическое отклонение. Какова
вероятность того, случайно подошедший
на остановку пассажир будет ожидать
автобус не более 4 минут, но и не менее
2 минут.
-
время ожидания автобуса - распределена
равномерно, найти среднее время ожидания
(математическое ожидание), среднее
квадратическое отклонение. Какова
вероятность того, случайно подошедший
на остановку пассажир будет ожидать
автобус не более 4 минут, но и не менее
2 минут.
Решение:
![]()
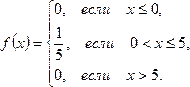
![]() ;
;
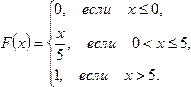
![]() .
.
