2. Полная группа событий. Пространство элементарных исходов. Примеры.

Полная группа событий.  Полной группой событий называется совокупность всех возможных результатов опыта. Теорема. Сумма вероятностей событий А₁ , А₂ , ..., А_n , образующих полную группу, равна единице:

Р (A₁) + Р (А₂) + ... + Р (А_n) = 1.

Пространство элементарных исходов

Теория вероятностей изучает случайные явления не непосредственно, а с помощью идеализированных математических моделей случайных опытов.

Всякий случайный опыт (испытание, эксперимент) состоит в осуществлении некоторого комплекса условий и наблюдении результата. Любой наблюдаемый результат опыта интерпретируется как случайный исход (случайное событие). Случайное событие в результате опыта может произойти, а может и не произойти.

Каждому опыту ставится в соответствие пространство элементарных исходов . Это множество простейших (т.е. неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов, таких, что результатом эксперимента всегда является один и только один исход.

Пример 1.1.1.

Опыт состоит в бросании одной правильной шестигранной игральной кости и наблюдении числа выпавших очков.

Элементарные исходы: {выпалоочков},.

Неэлементарные исходы (события): ={выпало чётное число очков},={выпало число очков, большее, чем 2} и т.п. Исходне является элементарным, т.к. он разлагается на более простые исходы.

Пространство элементарных исходов данного случайного опыта состоит из шести элементов.

3. Классическое определение вероятности события. Свойства вероятности события. Примеры.

Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равно­возможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р (А). В соответствии с определением P(A)=m/n , где m - число элементарных исходов, благоприятствующих событию А; n - число всех равновозможных элементарных исходов опыта, образующих полную группу событий. Это определение вероятности называют классическим.

Основные свойства вероятности. Пусть задано пространство элементарных событий  Е , а вероятности  Р  определены на событиях из  Е . Тогда:

Пример 1.

В урне 10 одинаковых по размерам и весу шаров, из ко­торых 4 красных и 6 голубых. из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?

Решение. Событие "извлеченный шар оказался голубым" обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию А. В соответствии с формулой P(A)=m/n , получаем P(A)=6/10=0,6

4. Статистическое определение вероятности события. Примеры. Теорема Бернулли (с доказательством).

Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.

w(A) – относительная частота (частость) события А;

m – число испытаний, в которых появилось событие А;

n – общее число испытаний.

Статистическое определение вероятности, как и понятия и методы теории вероятности, применимы только к тем событиям, которые обладают свойствами:

1. Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.

2. События должны обладать статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в серии испытаний относительная частота события меняется незначительно.

3. Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вероятность события Р(А) приближенно равной ее относительной частоте.

Пример. Английский учёный Пирсон произвел 23000 бросаний монеты, герб появился 11512 раз.

W(A) = = 0.5005

Теорема Бернулли.

Частость события в n повторных независимых испытаниях в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:

Cмысл теоремы состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость события m/n – величина случайная, как угодно мало отличается от неслучайной величины p – вероятности события, т.е. практически перестает быть случайной.

Доказательство:

	0	1
	q	p

Отметим, что случайная величина m =

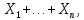
г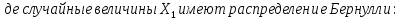

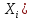E(=p ; D(=pq

Таким образом, выполняются все условия теоремы Чебышева, т.е.

.